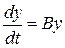Рассмотрим неуправляемую линейную систему

. (2.3)

Тогда преобразование 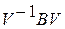(если оно существует) приводит систему (2.3) к диагональному виду

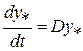. (2.4)

В системе (2.4) все уравнения разделяются

,… ,

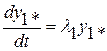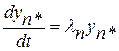интегрируются раздельно и имеют решения

,… ,

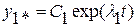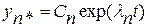где 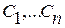- произвольные постоянные.

Если линейная система (2.3) приводится к диагональному виду (2.4), то фазовые переменные 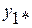,… 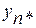называются главными координатами.

2.2. Управляемость динамических систем

Перед решением задачи оптимального управления динамической системой иногда (если это возможно) проводится анализ системы на управляемость.

Определение [6].

Динамическая система (1.1) является управляемой, если она может быть переведена из любого начального состояния 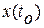в любое другое желаемое состояние 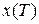за некоторый промежуток времени 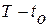путем приложения кусочно-непрерывного допустимого управления .

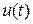Понятие управляемости и связанное с ним понятие наблюдаемости (оно будет рассмотрено ниже) впервые были введены Калманом [6].

Определить априори управляемость нелинейной динамической системы общего вида (1.1) не представляется возможным. Вывод об управляемости в этом случае делается в процессе решения задачи оптимального управления. Однако для линейной динамической системы (1.8) это можно сделать заранее. Наиболее известным является критерий управляемости Гильберта [6]. Этот критерий предполагает приведение линейной системы (1.8) к главным координатам (приводится часть системы, зависящая от фазовых переменных ).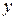

В соответствии с критерием Гильберта система (1.8), приведенная к главным координатам

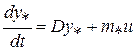, (2.5)

управляема, если ни одна из строк матрицы 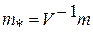не является нулевой (то есть для управляемости в каждой строке матрицы 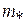должен быть по крайней мере один ненулевой элемент).

Если матрица 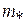представляет собой матрицу-столбец (это будет тогда, когда управление 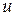- скалярная величина), то критерий управляемости требует, чтобы ни одна компонента этого столбца не была нулевой. Следовательно, для определения управляемости линейной системой (1.8) она должна быть приведена к главным координатам и представлена в виде (1.17). Система (1.8) приводится к виду (2.5), где 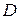диагональная матрица, тогда, когда матрица 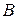имеет 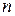линейно независимых собственных векторов (см. Приложение 1). В этом случае доказать неуправляемость системы, если хотя бы одна строка матрицы 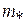нулевая, не представляет трудности. Поскольку взаимодействие между главными координатами в системе (2.5) отсутствует, то становится очевидным, что если любая строка, например 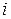-ая, равна нулю, то на соответствующую 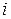-ую главную координату не может повлиять выбор управления. Следовательно, по этой переменной система неуправляема.

Если среди собственных значений матрицы 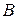есть кратные, то эта матрица, как известно [4], не может быть приведена к диагональной форме. Однако в этом случае она может быть преобразована к форме Жордана (см. Приложение 1). Тогда система (1.8) представляется в виде

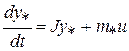. (2.6)

Здесь жорданова форма 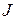матрицы 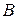имеет вид

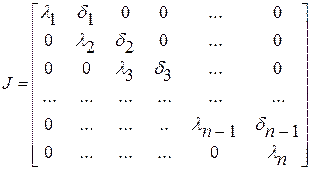, (2.7)

где компоненты 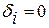, есл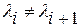и , и 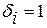, если .

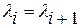В жордановой форме (2.7) обычно кратные собственные значения располагаются рядом. Поэтому в матрице 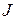имеются так называемые клетки Жордана. Так, например, двум кратным собственным значениям 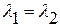соответствует клетка Жордана вида 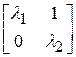, трем кратным собственным значениям 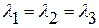- клетка Жордана вида

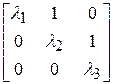
и т.д.

Если линейная динамическая система (1.8) приведена к виду (2.6), где 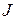- жорданова форма (2.7), то для управляемости необходимо, чтобы по крайней мере один элемент матрицы 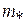в строке, соответствующей нижней строке каждой клетки Жордана, и как минимум один элемент матрицы 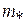в каждой другой строке (не входящей в клетку Жордана) были отличны от нуля [6].

Чтобы понять суть данного условия управляемости рассмотрим линейную систему третьего порядка с двумя кратными собственными значениями 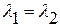, приведенную к форме (2.6). В случае скалярного управления 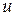она для этого случая примет вид

,

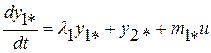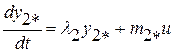, (2.8)

.

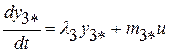Система (2.8) будет управляемой согласно сформулированному выше критерию, есл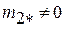и и 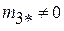. При этом элемент 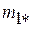может быть равен нулю: 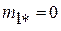. Здесь элемент 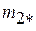соответствует нижней строке клетки Жордана, а элемент 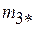соответствует строке матрицы Жордана, не входящей в клетку Жордана. Фазовая переменная 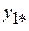оказывается управляемой, так как правая часть первого уравнения системы (2.8) зависит от переменной .

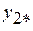Для определения управляемости линейной динамической системы (1.8) можно также воспользоваться критерием Калмана [6]. Этот критерий является менее наглядным, но с другой стороны более универсальным, так как его применение не зависит от того, имеются ли в системе кратные собственные значения или нет. В этом случае приведение системы к главным координатам не требуется. В соответствии с критерием Калмана для определение управляемости системы необходимо составить матрицу

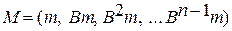(2.9)

размерностью 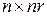, в которой ее составляющие матрицы соединяются по горизонтали.

В соответствии с критерием Калмана [6] система (1.8) будет управляема, если матрица 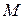(2.9) имеет ранг .

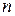Замечание. Ранг матрицы равен 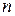, если по крайней мере один определитель этой матрицы 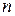-ого порядка отличен от нуля.

Следовательно, для определения управляемости системы (1.8), необходимо составить матрицу 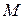(2.9) и определить ее ранг.

2.3. Наблюдаемость динамических систем

Понятие наблюдаемости дополняет понятие управляемости [6]. Эти два понятия, как правило, имеет смысл рассматривать только совместно. Если управляемость требует, чтобы каждое состояние (каждая переменная состояния 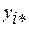, где 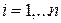) было чувствительно к управляющему воздействию 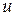, то наблюдаемость требует, чтобы каждая переменная состояния влияло на вектор измеренных переменных 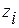, где .

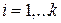Определение [6].

Система наблюдаема, если все ее переменные состояния 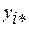можно непосредственно или косвенно (посредством других переменных 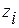) определить посредством измерений.

Получим критерий наблюдаемости для линейных динамических систем. Исходную систему уравнений (1.8) рассмотрим совместно с математической моделью измерительного устройства

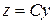, (2.10)

где матрица 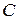определяет линейную связь между вектором состояния системы 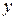и вектором измеряемых переменных .

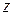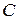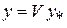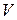В частном случае, когда матрица единична, переменные состояния непосредственно измеряются и система наблюдаема. В общем случае для определения наблюдаемости линейной системы (1.8) необходимо для анализа соотношения (2.10) перейти к главным координатам по формуле , где - определенная ранее матрица собственных векторов матрицы 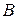. После проведения данного преобразования модель измерительного устройства (2.10) примет вид

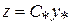, (2.11)

где .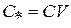

Тогда критерий наблюдаемости для системы (1.8) формулируется следующим образом: система (1.8) наблюдаема, если ни один из столбцов матрицы 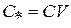не является нулевым.

Так, например, если первый столбец матрицы 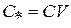нулевой, то переменная 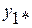не наблюдаема (от нее не зависит вектор 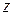измеряемых переменных). Данный критерий применяется тогда, когда система (1.8) приводится к диагональной форме (2.5) (то есть матрица 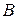не имеет кратных собственных значений).

Более универсальным методом определения наблюдаемости линейных систем является критерий, не требующий перехода к главным координатам [6]. В соответствии с этим критерием для определения наблюдаемости системы (1.8) необходимо составить матрицу

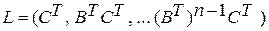. (2.12)

Система (1.8) будет наблюдаема, если матрица 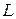будет иметь ранг .

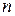3. ПРИНЦИП ДИНАМИЧЕСКОГО РОГРАММИРОВАНИЯ БЕЛЛМАНА И ТЕОРИЯ УСТОЙЧИВОСТИ ЛЯПУНОВА

3.1. Принцип динамического программирования Беллмана

Для определения оптимального управления линейными динамическими системами при решении задачи стабилизации могут быть применены различные методы [3]. Это могут быть классические методы вариационного исчисления, принцип оптимальности Беллмана [3], принцип максимума Понтрягина [2] и др. Здесь остановимся на изложении принципа динамического программирования Беллмана, с помощью которого были решены ряд важных практических задач оптимальной стабилизации движения объектов управления [3]. В основе метода динамического программирования лежит принцип оптимальности, сформулированный Р. Беллманом [7]. «Оптимальные стратегии управления обладают тем свойством, что каково бы ни было начальное состояние системы и управление в начальный момент, последующее управление должно быть оптимальным в смысле заданного критерия относительно любого другого состояния, которое могло бы явиться естественным следствием управления в начальный момент». Этот принцип для динамических систем (1.1) и (1.8) может быть сформулирован короче: любой отрезок оптимальной траектории есть тоже оптимальная траектория. Последнее означает, что независимо от того, каким было управление на начальном отрезке [ 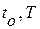], последующее управление на отрезке [ 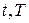] должно обладать свойством оптимальности по выбранному критерию. Следовательно, если ставится задача поиска оптимального управления на всем отрезке [ 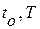], то управление 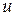должно быть оптимальным в каждый момент времени 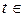[ 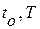]. Применение принципа оптимальности Беллмана для динамических систем (1.1) и (1.8) приводит к необходимости решения некоторого уравнения в частных производных – уравнения Беллмана относительно функции 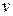вектора переменных состояния 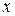(или 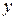). Данную функцию обычно называют производящей [3] и ее определение позволяет найти оптимальное управление 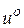как функцию от вектора состояния 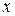(или 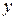), то есть решить задачу синтеза.

Выведем уравнение Беллмана для задачи быстродействия 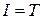при управлении динамической системой общего вида (1.1) [3]. Пусть 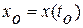- начальное положение системы (1.1). Необходимо найти управление 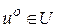, переводящее систему (1.1) из положения 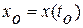в заданное положение 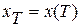за минимальное время. Возьмем некоторый момент времени 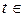[ 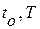]. Переход из состояния 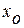в состояние 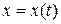осуществляется за время 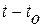(это время не обязательно минимально). Двигаясь затем из состояния 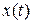в состояние 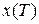оптимально затратим минимальное время 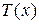. Общее время перехода будет равно 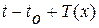. Пусть 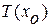минимальное время перехода из состояния 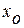в состояние 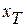, тогда справедливо неравенство 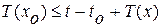или

,

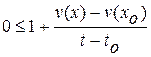где введено обозначение .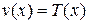

При 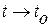получаем

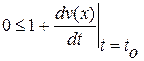
или 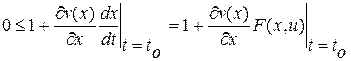. (3.1)

Так как начальная точка 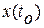была выбрана произвольно, то согласно принципу динамического программирования соотношение (3.1) должно быть справедливо для любой точки 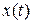, а не только для 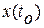. Следовательно, для любого момента времени 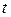имеем неравенство

,

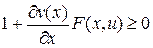где знак равенства соответствует оптимальной траектории.

Таким образом, оптимальное управление должно быть вычислено из условия

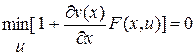. (3.2)

Определив из условия минимума (3.2) функцию 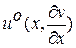и подставив в это же соотношение, получим дифференциальное уравнение в частных производных (уравнение Беллмана) в виде

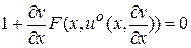(3.3)

относительно производящей функции .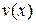

Решая уравнение (3.3) и, тем самым, определяя функцию 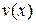, затем находим оптимальное управление 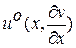, так как вид этой функции известен.

Замечание. При определении управления и при выводе уравнения Беллмана (3.3) было сделано два предположения: 1) о существовании оптимальной (в смысле быстродействия) фазовой траектории системы (1.1); 2) о непрерывности функции 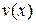и ее частных производных .

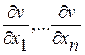Второе предположение при решении конкретных задач может оказаться слишком обременительным [2], особенно при решении задачи быстродействия. Дело в том, что функция управления 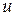, как правило, принадлежит некоторой области допустимых управлений 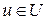, которая является замкнутой (содержит свои границы). Так, например, в простейшем случае, когда управление 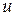скаляр, оно может удовлетворять неравенству 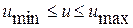. При построении управления часто оказывается, что оптимальное управление находится в классе кусочно-непрерывных функций и заключается в постоянном переключении управления с одного предельного значения на другое. В этом случае функция 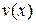становится не дифференцируемой в точках переключения управления и применение изложенного метода становится не обоснованным. Однако существуют модификации метода динамического программирования [3], а также другие методы (например, принцип максимума Понтрягина [2]), которые позволяют избежать эти трудности.

Рассмотрим более общий случай управления динамической системой (1.1), когда критерий оптимальности имеет вид

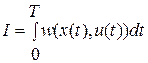, (3.4)

где функция 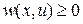является положительно определенной квадратичной формой векторов 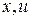. При этом функция 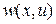обращается в ноль только при 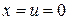. В частности, этому условию удовлетворяет функционал (1.9) линейной системы (1.8).

Введем новое время

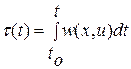, (3.5)

где в силу автономности системы (1.1) можно положить .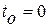

Тогда, дифференцируя соотношение (3.5) по времени, получим дифференциальное уравнение для нового времени

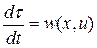. (3.6)

Переходя в системе (1.1) к интегрированию по новому времени 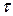, получим

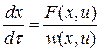. (3.7)

В этом случае критерий оптимальности примет вид

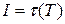, (3.8)

где 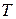- конечное время.

Следовательно, приходим к той же задаче быстродействия, только с другим временем 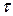. Здесь предполагается, что допустимые траектории системы (3.7) не проходят через точку 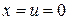. Исключение может составлять лишь конечная точка траектории (при 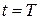) [3]. Тогда, применяя ту же схему вывода уравнения Беллмана, как для классической задачи быстродействия, получим

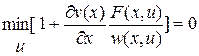
или

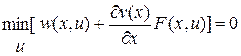. (3.9)

В этом случае схема определения оптимального управления методом динамического программирования состоит из двух этапов.

1. Определение из условия минимума (3.9) функции 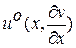(находится вид функции).

2. Подстановка этой функции в соотношение (3.9) и решение дифференциального уравнения в частных производных

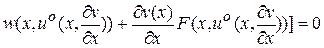(3.10)

относительно .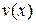

3. Определение оптимального управления 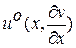в явном виде при известной функции .

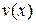3.2. Оптимальное управление линейными динамическими системами

Рассмотрим определение оптимального управления линейной динамической системой вида (1.8)

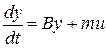, (3.11)

при решении задачи стабилизации (см. подробно раздел 1.4) с квадратичным критерием оптимальности

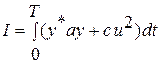. (3.12)

Здесь квадратная матрица 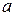удовлетворяет условиям Сильвестра (1.12), 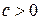- некоторая константа, 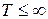- конечное время, 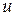- управление (скаляр), 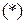- знак транспонирования, 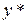- матрица-строка. В системе (3.11) матрица 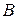и вектор 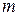считаются заданными (в общем случае они могут зависеть от времени ).

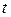Ставится задача об оптимальном переводе системы (3.11) из начального положения 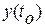в начало координат 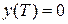. Для решения этой задачи используется принцип Беллмана (3.9), который для линейной системы (3.11) и критерия (3.12) приводит к соотношению

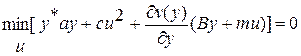. (3.13)

Выражение, стоящее под знаком минимума в соотношении (3.13), представляет собой квадратичную функцию управления 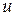. Выделяя слагаемые, зависящие только от управления, получим

.

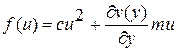Необходимое условие минимума этой функции по управлению будет иметь вид

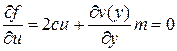. (3.14)

Причем выполняется достаточное условие минимума

.

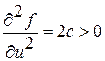Поэтому оптимальное управление определится из условия (3.14) в виде

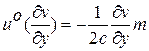, (3.15)

где выражение 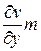рассматривается как скалярное произведение векторов 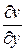и 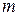, то есть

.

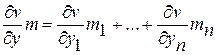Подставляя управление (3.15) в условие (3.13) и приводя подобные члены, получим уравнение Беллмана для линейной динамической системы (3.11)

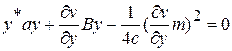. (3.16)

В этом случае определение оптимального управления для линейной системы осуществляется следующим образом: 1) из уравнения в частных производных (3.16) находится функция 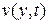; 2) функция 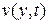подставляется в выражение (3.15) и определяется оптимальное управление .

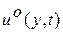После подстановки оптимального управления 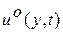в исходную систему (3.11) решения полученной замкнутой системы должны удовлетворять (в соответствии с постановкой задачи стабилизации) некоторым условиям устойчивости, в частности, они должны стремится с течением времени к началу координат 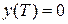. Здесь следует отметить, что уравнение Беллмана (3.16) может иметь несколько решений 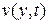. Необходимо из этих возможных решений выбрать такое, которое будет обеспечивать указанное выше условие устойчивости. Выбор необходимого решения может быть осуществлен на основе теории устойчивости Ляпунова А.А. [4], которая будет изложена ниже.

3.3. Теория устойчивости Ляпунова

Основополагающие понятия Ляпунова А.А. об устойчивости движения динамических систем и методы, позволяющие устанавливать свойства устойчивости, находят непосредственное применение при решении задачи стабилизации, сформулированной выше.

Рассмотрим уравнения возмущенного движения (1.6), записав их в виде

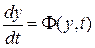, (3.17)

где вектор 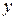определяет отклонения от невозмущенного движения 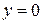, при этом в силу вида системы (1.6) .

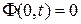Причем в форме (3.17) может быть записана как исходная система (1.1) без управления 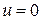, так и система с выбранным управлением 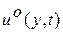. И в том и в другом случае нас будут интересовать свойства устойчивости некоторого частного решения системы (1.1) 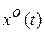, то есть поведение вектора отклонений .

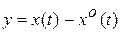Определение (устойчивость по Ляпунову А.А.) [4].

Невозмущенное движение 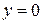называется устойчивым по Ляпунову, если для любого заданного числа 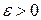, как бы оно мало не было, найдется другое число 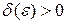такое, что выполнение неравенства

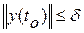
влечет за собой как следствие выполнение неравенства

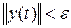
при любом 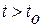; в противном случае невозмущенное движение неустойчиво.

В этом определении обозначения 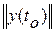и 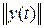означают евклидову норму вектора отклонений 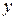в начальный 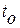и текущий 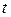моменты времени, например,

.

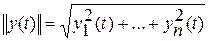Так как уравнения 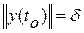и 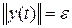в пространстве переменных 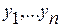задают гиперсферы, то геометрическое истолкование устойчивости по Ляпунову следующее: каково бы не было число 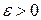, а значит какова бы не была заданная сферическая область в пространстве переменных 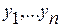, найдется такое число 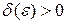, что если начальное положение системы (1.39) находится внутри или на поверхности сферы 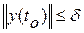, то фазовая траектория системы (1.39) будет находиться внутри сферы 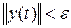во все время движения системы .

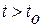Определение(асимптотическая устойчивость) [4].

Невозмущенное движение 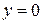устойчиво асимптотически, если 1) оно устойчиво по Ляпунову; 2) выполняется предельное равенство

.

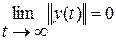Сформулируем здесь основные теоремы так называемого прямого (второго) метода Ляпунова решения задач устойчивости для системы (3.17). Теоремы эти основываются на свойствах некоторых скалярных функций 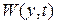, которые определяются следующим образом.

Определение [4]. Функция 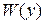называется знакоопределенной положительной (положительно определенной) в некоторой области 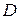, если 1) 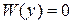только при 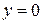, 2) 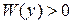всюду в 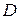при .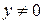

Пример: .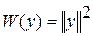

Определение. Функция 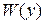называется знакоопределенной отрицательной (отрицательно определенной) в некоторой области 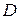, если функция 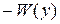является знакоопределенной положительной.

Определение. Функция 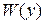называется знакопостоянной положительной (отрицательной) в некоторой области 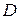, если она неотрицательна (неположительна) в этой области.

Пример знакопостоянной положительной функции: .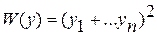

Определение. Функция 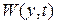, зависящая от времени 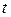, называется знакоопределенной положительной в некоторой области 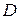, если найдется другая знакоопределенная положительная функция 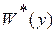такая, что соблюдается неравенство 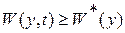при всех 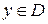и .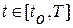

Говорят, что знакоопределенная положительная функция 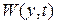допускает бесконечно малый высший предел, если существует знакоопределенная положительная функция 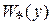такая, что выполняется неравенство 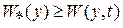при всех 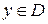и .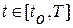

Знакоопределенные функции 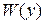обладают тем свойством, что равенство 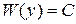(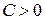) задает в пространстве переменных 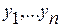замкнутую гиперповерхность, если постоянная 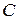достаточно мала.

Если функция 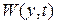знакоопределенная положительная и имеет бесконечно малый высший предел, то поверхность 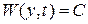, зависящая от времени, располагается в слое 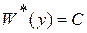, , 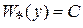так как .

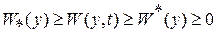Теорема 1 (об устойчивости по Ляпунову) [4].

Если уравнения движения системы (3.17) таковы, что можно найти знакоопределенную положительную функцию 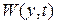, полная производная которой

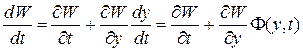, (3.18)

вычисленная в силу этих уравнений, есть знакопостоянная отрицательная функции или тождественно равная нулю, то невозмущенное движение 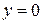устойчиво по Ляпунову.

Доказательство теоремы 1 в случае, когда функция 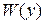не зависит от времени (это имеет место, например, для автономных систем, правые части которых не зависят от времени) сравнительно простое [4]. Действительно, в этом случае

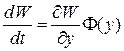
есть скалярное произведение вектора градиента функции 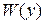с компонентами (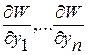) и вектора скорости (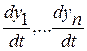) изображающей точки в фазовом пространстве. По условию производная 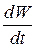отрицательна или нуль. С учетом того, что вектор градиента всегда направлен по нормали к поверхности 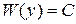в сторону возрастания функции 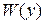, то траектории системы пересекают (в силу отрицательности скалярного произведения) замкнутую поверхность 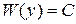из вне во внутрь или располагаются на ней (если 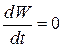). В любом случае при любом 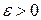всегда можно выбрать 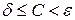такое, что если неравенство 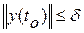выполняется при условии 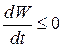, то любая траектория системы может покинуть поверхность 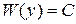только в сторону убывания 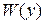, и неравенство 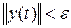будет соблюдаться при любом 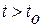, что и требовалось доказать.

Теорема 2 (об асимптотической устойчивости) [4].

Если уравнения движения системы (3.17) таковы, что можно найти знакоопределенную положительную функцию 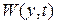, допускающую бесконечно малый высший предел при 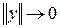и имеющую знакоопределенную производную по времени в силу этой системы, то невозмущенное движение 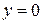асимптотически устойчиво.

Доказательство теоремы 2 достаточно простое [4] в случае, когда функция 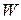не зависит от времени. Так как производная 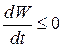и обращается в ноль только в начале координат 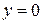, то любая траектория системы будет пересекать поверхность 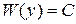снаружи внутрь. Поскольку число 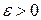можно выбирать сколь угодно малым, то такое поведение траекторий можно проследить до момента прихода их в точку 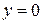, отсюда следует теорема 2.

Теоремы 1 и 2 составляют основу прямого (второго) метода Ляпунова исследования устойчивости невозмущенного движения системы (3.17).

3.4. Связь метода динамического программирования с теорией устойчивости Ляпунова

Допустим, что в результате решения уравнения Беллмана (3.16) определена какая-либо функция 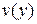и отвечающая ей управление 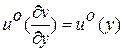. Подставим это управление в систему (3.11) и в уравнение (3.13), тогда

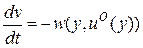, (3.19)

где 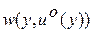- подинтегральная функция в критерии (3.12).

По определению 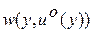- знакоопределенная положительная функция. С другой стороны, если удастся удовлетворить уравнение Беллмана (3.16) какой-либо знакоопределенной положительной функцией 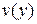, то эта функция будет функцией Ляпунова для системы (3.11). Причем она будет соответствовать условиям теоремы 2 об асимптотической устойчивости второго метода Ляпунова, что следует из уравнения (3.19). В этом случае замкнутая система, получающаяся подстановкой управления 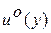в систему (3.11), будет обладать свойством асимптотической устойчивост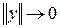и при 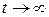. Если время 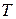конечно 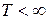, то можно воспользоваться преобразованием [3]

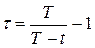, (3.20)

вводя новое время 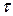. В этом случае 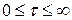, а система (3.19) примет вид

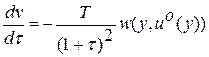, (3.21)

и преобразование (3.20) не меняет знака 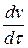. Поэтому и при 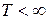формально функцию 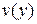можно трактовать как функцию Ляпунова, удовлетворяющую теореме 2 об асимптотической устойчивости. Отсюда следует следующая

Теорема 3 [3].

Для того, чтобы управление 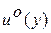, определенное методом динамического программирования, давало оптимальное решение задачи стабилизации, достаточно, чтобы соответствующая ему функция 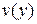1) удовлетворяла уравнению Беллмана (3.16), 2) была функцией Ляпунова для замкнутой системы.

Функцию 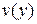, удовлетворяющую условиям этой теоремы, обычно называют оптимальной функцией Ляпунова [3].

4. ОПРЕДЕЛЕНИЕ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ ДЛЯ ЛИНЕЙНЫХ ДИНАМИЧЕСКИХ СИСТЕМ

4.1. Решение уравнения Беллмана для линейных стационарных динамических систем

Уравнение Беллмана (3.16) для линейной динамической системы (3.11), где матрица 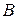и вектор 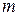для стационарного случая не зависят от времени 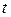, можно удовлетворить квадратичной формой [3]

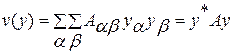, (4.1)

где 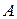- симметричная матрица.

Для определения решения в виде (4.1) необходимо подставить выражение (4.1) в уравнение (3.16) и приравнять коэффициенты при подобных слагаемых по переменным 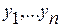. Можно доказать следующие тождества.

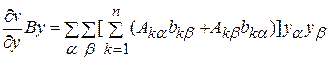, (4.2)

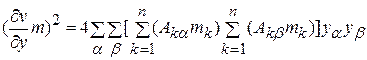. (4.3)

Подставляя выражения (4.2), (4.3) в уравнение Беллмана (3.16), получим

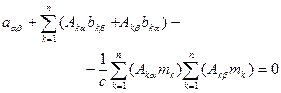, (4.4)

где индексы 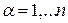, 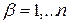и 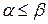в силу симметричности матриц 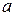и .

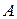Поэтому выражения (4.4) представляют собой систему алгебраических нелинейных уравнений для определения всех коэффициентов 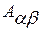(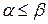) симметричной квадратичной формы (4.1). Как нетрудно установить количество уравнений, входящих в систему (4.4), равно .

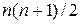Очевидно, система (4.4) может иметь несколько решений, из которых следует выбрать такое решение, которое удовлетворяет условиям Сильвестра

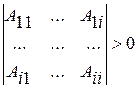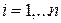. (4.5)

В этом случае функция (4.1) будет знакоопределенной положительной. Тогда в соответствии с теоремой 3 функция 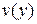будет являться функцией Ляпунова для замкнутой системы. Следовательно, определяя оптимальное управление из выражения (3.15), получим

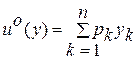. (4.6)

Здесь

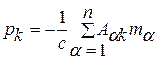, (4.7)

где .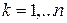

В этом случае коэффициенты 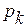называют коэффициентами усиления автомата стабилизации. Таким образом, управление, стабилизирующее систему (3.11) при условии минимума квадратичного критерия (3.12), является линейным с коэффициентами усиления (4.7).

4.2. Решение уравнения Беллмана для линейных нестационарных динамических систем

При рассмотрении линейных нестационарных систем предполагается, что матрица 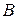и вектор 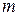зависят от времени 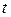вследствие зависимости от времени программного оптимального управления (см. раздел 1.2). В этом случае перепишем систему (1.8) в следующем виде

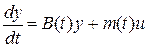, (4.8)

где 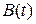и - и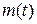звестные функции времени.

Решается та же задача оптимального управления о переводе системы (4.8) из начального положения 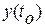в начало координат 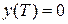с критерием оптимальности

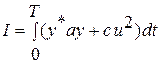. (4.9)

Решение данной задачи проводится также как для стационарной системы (3.11), отличие лишь заключается в том, что функция 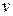явно зависит от времени: 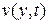. Поэтому соотношение (3.9), выражающее принцип оптимальности Беллмана, для системы (4.8) примет вид

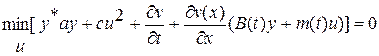. (4.10)

Так как слагаемые, зависящие от управления 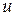, остались теми же как для стационарного случая, то вид оптимального закона управления тот же

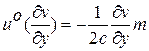. (4.11)

Подставляя выражение (4.11) в соотношение (4.10), получим уравнение Беллмана для нестационарной линейной системы (4.8)

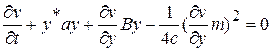. (4.12)

Решение уравнения Беллмана (4.12) ищем в виде квадратичной формы [3]

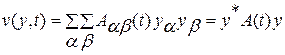, (4.13)

где 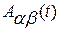- определяемые компоненты матрицы .

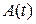Далее необходимо подставить квадратичную форму (4.13) в уравнение (4.12) и приравнять коэффициенты при одинаковых слагаемых. В результате получим

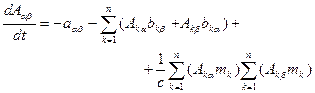, (4.14)

где , 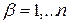и .

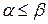Систему обыкновенных дифференциальных уравнений (4.14) необходимо проинтегрировать по времени. В работе [3] предлагается определять коэффициенты 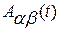методом численного интегрирования с учетом требуемых конечных граничных условий 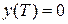. Тогда можно задать 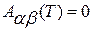и проинтегрировать систему (4.14) обратно с отрицательным шагом до начального времени 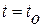. Если 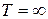, то время 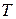берется достаточно большим, чтобы при его изменении в большую сторону величины 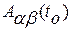практически не изменялись. После того, как с помощью этого способа определены функции 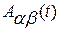, управление определяется из выражения (4.11) в виде

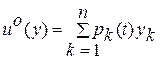. (4.15)

Здесь

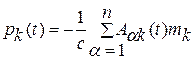, (4.16)

где .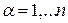

4.3. О выборе критерия оптимальности при решении задачи стабилизации

При решении задачи оптимальной стабилизации систем (1.8) и (4.8) предполагалось, что критерий оптимальности (4.9) выбран заранее и вид его известен. Фактически выбор критерия должен производить специалист, проектирующий систему стабилизации. Если подинтегральная функция в интеграле (4.9) не принимает отрицательных значений, то критерий (4.9) выражает меру отклонения действительного движения от номинального программного движения. Искомый закон управления должен обеспечить минимизацию этой меры вдоль всей программной траектории системы. Если структура критерия (4.9) известна, то необходимо задать матрицу 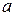и коэффициент 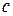. Оказывается, выбирая эти параметры, можно удовлетворить некоторым требованиям, которым должен удовлетворять переходный процесс в системе. Эти требования иногда называют вторичными критериями оптимальности [3]. Перечислим наиболее важные из них.

1. Критерий «время регулирования». Даны две сферы

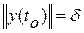и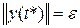

такие, что 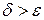. Рассмотрим все множество допустимых управлений 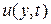, при которых фазовая точка, начинающая свое движение на первой сфере, приходит под действием управления на вторую сферу и остается внутри нее при любом 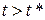. Такое время всегда существует, поскольку замкнутая система асимптотически устойчива. Будем называть 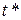временем регулирования. В общем случае можно ввести некоторое ограничение

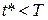, (4.17)

где 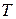- заданное число.

Ограничение (4.17) отбирает среди всех допустимых управлений те, которые гарантируют замкнутой системе определенную быстроту затухания переходного процесса.

2. Критерий монотонности. Этот критерий обеспечивает некоторые определенные свойства гладкости переходному процессу, например, апериодичность. Апериодичность для линейной замкнутой системы достигается, если ее собственные значения вещественны и отрицательны (см. Приложение 2). В этом случае переходный процесс не обладает колебательными свойствами.

3. Критерий, учитывающий ограничения, накладываемые на управления 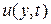. Например, допустимые управления могут принадлежать некоторой области 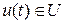. В случае скалярного управления эта область может быть задана в виде неравенства

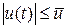, (4.18)

где 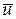- заданная величина.

4. Критерий, обеспечивающий принадлежность фазовой траектории заданной области. С помощью этого критерия можно удовлетворить некоторым ограничениям, накладываемым на фазовые переменные замкнутой системы. Например, можно сформулировать требование, чтобы фазовые переменные удовлетворяли неравенствам

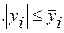, (4.19)

где 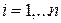; 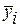- заданные числа.

5. Критерий, учитывающий ограничение на производные функции управления. Например, могут быть заданы неравенства

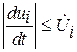, (4.20)

где 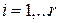; 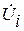- заданные числа.

Существуют также другие вторичные критерии переходного процесса [3].

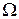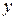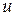Задача выбора управления с учетом некоторых перечисленных вторичных критериев (или ограничений) может быть сформулирована следующим образом [3]. Рассмотрим множество определенно положительных по и функций 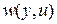, входящих в основной критерий

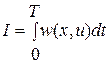. (4.21)

Примером множества