Рассмотрим методику определения количественной оценки результатов измерения методом математической статистики.
Положим, что в результате измерений физической величины имеется массив из n случайных величин:
n1; n2; n3; n4; n5; n6; n7; ……..; n100.
Выявляем в этом массиве чисел минимальное и максимальное числа. Допустим, в процессе измерения напряжения получили 100 значений случайных величин, минимальное значение составило 1510 мм, а максимальное – 1550 мм, т.е. все случайные величины распределяются в диапазоне от 1510 до 1550 мм.
Разбиваем этот диапазон чисел на 10 интервалов: (1550-1510): 10 = 4 мм, присваиваем каждому интервалу свой номер, подсчитываем количество чисел в каждом из интервалов (nk) и вносим полученные данные в таблицу 6.1. В третьей строке таблицы записываются значения nk / n.
Затем строим гистограммы наблюдений в виде графика в координатах nk/n – интервалы значений (рис. 6.2).
Таблица 6.1 - Выборка вариационного ряда
| № п/п | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| интервал | - | - | - | - | - | - | - | - | - | - |
| nk | ||||||||||
| nk/n | 0.01 | 0.02 | 0,10 | 0,14 | 0,20 | 0,20 | 0,18 | 0,12 | 0,02 | 0,01 |
Гистограмма распределения значений ширины колеи
|
|
|
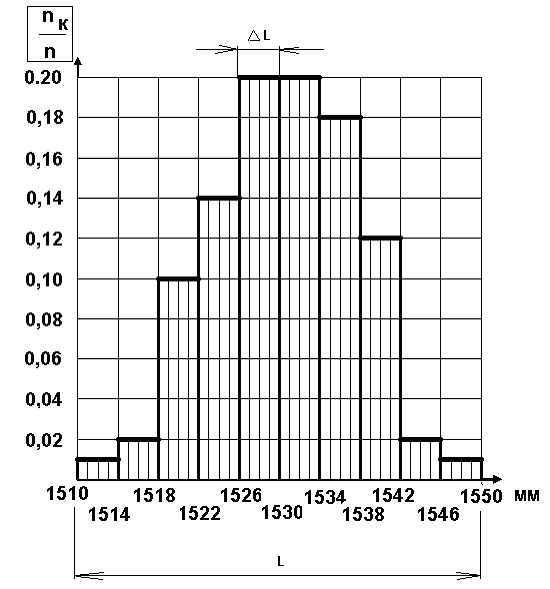
Рис. 6.2
Приняв общую площадь, ограниченную гистограммой распределения равной единице S0 = 1,диапазон изменения - за L,а интервал - за ∆l, можно определить частоту попадания результатов наблюдений в тот или интервал как отношение площади соответствующего прямоугольника шириной ∆l к общей площади S0.
Если гистограмму распределения случайных величин описать плавной кривой, то получим кривую плотности распределения вероятностей случайной величины, которую можно записать в нормированном виде:
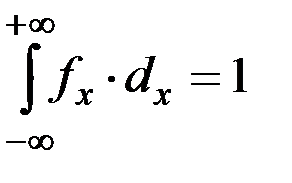 /6.1./
/6.1./
Далее обычно подбирают закон распределения ближе всех описывающий свойства данной случайной величины.
Существуют несколько теоретических законов распределения:
1. Нормальный закон распределения (кривая Гаусса).
2. Треугольный закон распределения (закон Симпсона).
3. Равномерный закон распределения.
4. Закон распределения Стьюдента.
5. Закон распределения Коши и т.д.
В практике большинство распределений подчиняются закону нормального распределения. В аналитической форме этот закон выражается формулой:
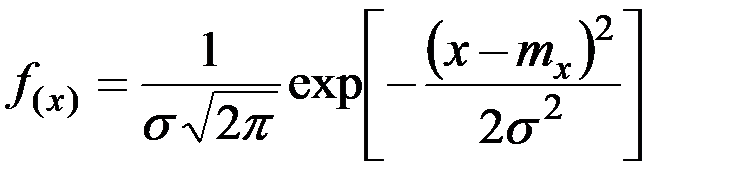 /6.2./
/6.2./
где х – случайная величина;
mx – математическое ожидание случайной величины;
σ – среднеквадратическое отклонение.
Для массива случайных величин равного n
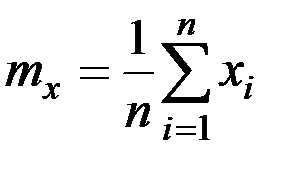 /6.3./
/6.3./
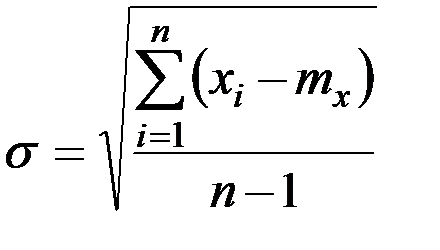 /6.4./
/6.4./
После статистической обработки истинным значением величины считается математическое ожидание mx, а разброс параметров оценивают по величине среднеквадратического отклонения σ.
|
|
|
Зная величину истинного значения mx, вычисляют абсолютную погрешность каждого из n наблюдений:
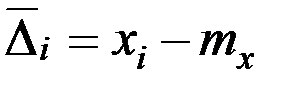 /6.5./
/6.5./
и находят среднеквадратическое отклонение, характеризующее точность метода измерения:
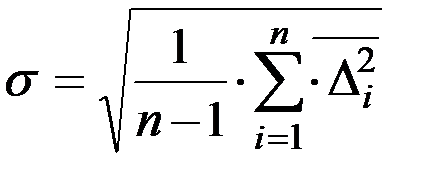 /6.6./
/6.6./
 2015-04-01
2015-04-01 791
791








