Функции

В GPSS рассматриваются пять типов функций:

D – дискретная числовая;

C – непрерывная числовая;

L – табличная (списковая) числовая;

E – дискретная атрибутивная;

M – табличная (списковая) атрибутивная.

Рассмотрим два первых типа функций.

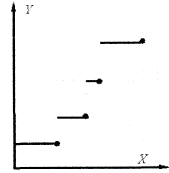
Дискретная функция – кусочно-постоянная функция, которая состоит из горизонтальных ступеней (рис. 1.2, а).

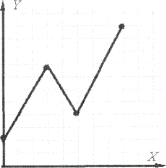
Непрерывная функция – кусочно-непрерывная функция, в GPSS она состоит из соединенных между собой прямых отрезков и представляет собой ломаную линию (рис. 1.2, б).

а б

Рис. 1.2. Графики дискретной (а) и непрерывной (б) функций

Для того чтобы задать дискретную функцию, необходимо задать координаты крайних правых точек горизонтальных отрезков. Для непрерывной функции необходимо задать координаты всех точек, которые являются концами отрезков.

Для определения дискретной и непрерывной GPSS-функций необходимо:

1. Присвоить функции имя (числовое или символьное).

2. Задать аргумент функции. Аргументом могут быть ссылка на генератор случайных чисел, используемый для розыгрыша в соответствии c распределением, заданным функцией; стандартный числовой атрибут; ссылка на любую другую функцию.

В первом случае аргумент задается в виде RNj, где j – целое число (номер генератора). В GPSS World количество идентичных генераторов случайных чисел неограничено, а выдаваемые ими значения лежат в диапазоне от 0 до 0,999999.

3. Задать тип функции и число крайних точек функции;

4. Задать значения аргумента (переменной) и соответствующие значения функции (т. е. координаты крайних точек функции).

Три первых элемента указываются в операторе определения функции FUNCTION, который имеет следующий формат:

метка FUNCTION А,В,

где метка – имя функции (числовое или символьное);

А – RNj (j = 1,...) или СЧА;

В – Dn либо Сn, где D определяет дискретную функцию, С – непрерывную функцию; n – для дискретной функции – число различных значений, получаемых функцией (количество горизонтальных отрезков); для непрерывной функции – число, на единицу больше числа отрезков, составляющих функцию (количество точек).

За каждым оператором описания FUNCTION следуют операторы задания координат точек функции (значений аргументов X_iи соответствующих им значений функции Y_i), называемые операторами описания координат функции; они имеют следующий формат записи:

если координаты всех точек расположены в одной строке оператора описания функции, то записывают: X₁, Y₁/ X₂, Y₂/…/X_n, Y_n;

если координаты точек расположены в нескольких строках оператора описания функции, то записывают:

X₁, Y₁/X₂, Y₂/…/ X_i, Y_i

X_i+1, Y_i+1/X_i+2, Y_i+2/…/X_k, Y_k

……

X_m+1, Y_m+1/X_m+2, Y_m+2/…/X_n, Y_n,

где X_i и Y_i – координаты i-й точки функции (в случае моделирования случайной величины X_i является i-й суммарной (кумулятивной) частотой; Y_i – соответствующим значением случайной величины).

Основной единицей информации оператора описания координат функции является пара значений – X_i и Y_i (координаты точки i).

Значения координат X_i и Y_i одной точки функции разделяются запятой. Последовательные наборы координат разделяются знаком «/».

Координаты X_i и Y_i, относящиеся к одной точке, задаются в одной строке оператора описания функции, т. е. пара координат одной точки не должна разрываться.

Все строки описания координат функции должны начинаться c первой позиции.

Во всех случаях значения аргумента должны удовлетворять следующим неравенствам: Х₁ ≤ Х₂ ≤ Х₃ ≤ … ≤ Х_n.

Значение функции является ее стандартным числовым атрибутом. Если имя функции числовое, то к значению функции обращаются через FNj (где j – номер функции), если имя символьное – через FN$<имя функции>. Аргументом функции может быть и значение какой-либо другой функции. Каждая функция должна иметь, по крайней мере, две описанные точки.

П р и м е р [1]. Пусть необходимо смоделировать дискретную случайную величину (д. в.), значения которой приведены в табл. 1.3. Согласно этой таблице д. в. должна получать значения 2, 5, 8, 9, 12 с частотой 0,15; 0,2; 0,25; 0,22; 0,18 соответственно.

Т а б л и ц а 1.3. Значения дискретной величины (д. в.)

Значение случайной д. в.	Относительная частота появления д. в.	Суммарная частота	Диапазон появления д. в.	Номер диапазона появления д. в.
	0,15	0,15	[0,0 – 0,15]
	0,20	0,35	(0,15 – 0,35]
	0,25	0,60	(0,35 – 0,60]
	0,22	0,82	(0,60 – 0,82]
	0,18	1,00	(0,82 – 1,0]

GPSS-функцию можно определить так:

RASP FUNCTION RN4,D5

.15,2/.35,5/.6,8/.82,9/1,12,

где X_i – значения точек, определяющих интервалы изменения функции; Y_i – значения самой функции RASP. В качестве источника случайных чисел выступает RN4. Случайная д.в. может иметь пять различных значений. Суммарные частоты и соответствующие им пять значений функции записаны как пять пар чисел.

Особенности вычисления непрерывных и дискретных GPSS - функций: в начальной фазе выполняемые действия при вычислении дискретной и непрерывной функции одинаковы. При обращении к функции определяется значение ее аргумента. Затем просматривается упорядоченный ряд значений Х₁ < Х₂ <... < Х_i <... < Х_nдля определения интервала, в который попало значение аргумента (пусть это будет отрезок [i – 1; i]). Если функция дискретная, то второй элемент соответствующей пары X_i и Y_iявляется значением функции. Если функция непрерывная, то выполняется линейная интерполяция для пары точек (i – 1) и i,находящихся на краях интервала значений функции, на который указало значение аргумента. Интерполяция производится согласно выражению:

,

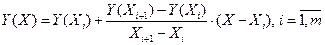где m – число точек функции.

Целая частьрезультата интерполяции является значением функции.

Если значение аргумента функции больше значения координаты Х_nпоследней точки, то в обоих случаях (дискретной и непрерывной функции) значениями функции являются значения Y_n.

П р и м е р. Необходимо промоделировать случайную величину, равномерно распределенную на отрезке [2; 5]. Для получения случайных чисел при непрерывном равномерном распределении используется функция типа С.

Так как непрерывная функция задается с помощью линейной интерполяции, для всех точек на одном интервале значений суммарной частоты существует одинаковая вероятность их использования. Это делает процедуру розыгрыша случайной величины при равномерном непрерывном распределении чрезвычайно простой.

Предположим, что некоторая случайная переменная распределена равномерно и непрерывно на интервале от 2 до 6 (исключительно). Вероятность того, что значение переменной меньше 2, равна 0, а вероятность того, что она меньше 6, равна 1. Эти два значения суммарной вероятности используются для определения непрерывной функции на отрезке [2; 5]:

INN FUNCTION RN2,C2

0,2/1,6

Несмотря на то, что значением второй пары, использованной при определении функции, является 6, функция никогда не получает значение 6. потому что максимальное значение, которое может выдать генератор случайных чисел, равно 0,999. Таким образом, наибольшей целой частью получаемого значения является 5. В случае, если генератор случайных чисел RN2 выдаст, например, значение 0,4, GPSS-функция INN примет значение 3.

Точные граничные значения RN2, соответствующие возможным значениям функции INN, представлены в табл. 1.4.

Т а б л и ц а 1.4. Граничные значения генератора RN2

Целая часть значения функции	Диапазон значений RN2
	[0,0 – 0,25]
	(0,25 – 0,50]
	(0,50 – 0,75]
	(0,75 – 0,999]

Преимущество непрерывной функции по сравнению с дискретной функцией очевидно, если в результате розыгрыша требуется получать целые числа. Если в этих целях воспользоваться дискретной функцией, то нужно будет рассчитать для рассмотренной задачи 4 значения суммарных частот и задать 4 пары для определения функции. Очевидно, что с увеличением диапазона будет увеличиваться количество пар значений, которые необходимо задать и рассчитать.

Равномерное распределение [2, 3, 4, 5] не может быть реализовано непосредственно c помощью операндов А и В блока GENERATE. Заданы четыре возможных значения, тогда как интервал А ± В (А и В – целые числа) всегда имеет нечетное число элементов.

Рассмотрим моделирование неравномерных случайных величин при использовании функций в блоках GENERATE и ADVANCE. Пусть распределение интервалов поступления транзактов через определенный блок GENERATE или время задержки в некотором блоке ADVANCE не является равномерным (либо является равномерным c «плавающими во времени», т. е. нефиксированными, значениями среднего и половины поля допуска). Для входов транзактов в модель через блок GENERATE и для задания закона времени задержки в соответствующем блоке ADVANCE необходимо использовать функции и (или) СЧА. Использование функций, заданных в операндах блоков, зависит от контекста. От значения функции берется целая часть, за исключением тех случаев, когда это значение используется в качестве операнда В блоков GENERATE и ADVANCE или в качестве операнда C блока ASSIGN.

Различные варианты использования функций и СЧА в качестве операндов А и В блоков GENERATE и ADVANCE приведены в табл. 1.5.

Т а б л и ц а 1.5. Варианты использования функций и СЧА
в качестве операндов А и В блоков GENERATE и ADVANCE

Операнд	Значение интервала поступления транзактов или их задержки
А	В
α (число или СЧА)	β (число или СЧА)	Генерируется случайное число, равномерно распределенное на интервале α ± β. Результат равен полученному числу
FN$DIS	–	Результат равен значению функции DIS
–	FN$B	Данная комбинация недопустима
FN$DIS	β (число или СЧА)	Вначале вычисляется значение функции DIS. Берется целая часть этого значения (пусть это будет число α), после чего генерируется случайное число, равномерно распределенное на интервале α ± β. Результат равен полученному числу
α (число или СЧА)	FN$DIS	Вначале вычисляется значение функции DIS (пусть это будет число β, после чего определяется произведение α × β. Результат равен целой части этого произведения
FN$DIS1	FN$DIS2	Вычисляются значения функций DISl и DIS2 (пусть это будет числа α и β), после чего определяется произведение α × β. Результат равен целой части этого произведения

П р и м е р использования функции в качестве операнда:

TIME FUNCTION RN2,D5

.05,5/.15,6/.75,8/.93,9/1,10

Функция TIME является дискретной (D5), значения аргумента – равномерно распределенная величина в диапазоне от 0 до 0,999 (RN2), заданы интервалы определения функции и ее значения. Данную функцию можно вызвать:

GENERATE FN$TIME

…

ADVANCE FN$TIME

П р и м е р задания функции в блоке ADVANCE [4]. Пусть в моделируемой системе время обслуживания некоторым устройством распределено равномерно на интервале A ± 2, где среднее время обслуживания A c вероятностью 0,4 принимает значение 5, a c вероятностью 0,6 – значение 7.

Определим функцию AVERAGE_T:

AVERAGE_T FUNCTION RN1,D2

.4,5/1,7

Используем AVERAGE_T в блоке ADVANCE:

ADVANCE FN$AVERAGE_T,2

Выполнение подпрограммы блока ADVANCE включает в себя расчет функции AVERAGE_T, а это в свою очередь требует обращения к генератору случайных чисел RN1. Пусть генератор выдал значение, меньшее чем 0,4. Тогда соответствующее значение функции AVERAGE_T равно пяти. Таким образом, время задержки текущего транзакта в устройстве будет равномерно распределено на интервале 5 ± 2.

На практике обычно достаточно, чтобы все случайные переменные имели конечное число конкретных значений. Следовательно, возможна дискретизация непрерывных распределений, после чего они могут быть определены в GPSS c помощью дискретных и непрерывных GPSS-функций.

В системе GPSS World для задания различных вероятностных функций распределения можно использовать библиотечные процедуры, написанные на языке PLUS, однако использование вероятностных распределений в табличном виде значительно ускоряет процесс моделирования.

Рассмотрим табличный способ задания пуассоновского потока заявок. Вероятность поступления k заявок пуассоновского потока в течение интервала t составляет 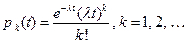, где λ – интенсивность потока. Интервалы времени между соседними заявками пуассоновского потока распределены по экспоненциальному закону. Согласно методу обратной функции [4]можно получить ряд чисел, которые имеют экспоненциальное распределение, если ряд случайных чисел R,равномерно распределенных на интервале [0, 1], преобразовать в соответствии c функцией, обратной к экспоненциальной функции распределения:

,

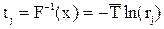где t_j – j-й разыгранный интервал времени поступления;

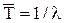– средний интервал времени поступления;

r_j – j-e число в последовательности случайных чисел R c равномерным распределением на интервале [0, 1].

Разработчиками GPSS была осуществлена аппроксимация функции
F^-1(x), обратной к экспоненциальной функции распределения c параметром λ, равным единице. Функция F^-1(x)была заменена двадцатью тремя отрезками, которые использовались для преобразования значений RNj в значения ln(RNj).

П р и м е р ы задания и использования экспоненциальной функции распределения.

1. Функция XPDIS определяет экспоненциальное распределение c параметром λ = 1:

XPDIS FUNCTION RN1,C24

0,0/.1,.104/.2,.222/.3,.355/.4,.509/5,.69/.6,.915/.7,1.2/

/75,.1.38/.8,1.6/.84,1.83/.88,2.12/.9,2.3/.92,2.52/.94,2.81/

.95,2.99/.96,3.2/.97,3.5/.98,3.9/.99,4.6/.995,5.3/.998,6.2/.999,7/9998,8

2. Пуассоновский входящий поток c интенсивностью λ, отличной от единицы, моделируется c помощью блока GENERATE следующим образом: в качестве операнда А используют среднее значение интервалов времени поступления T = 1/λ, где λ – интенсивность пуассоновского потока; в качестве операнда В используют СЧА – значение функции XPDIS, операторы определения и описания которой приведены выше.

Пусть среднее значение интервалов поступления Тв пуассоновском потоке требований равно 2 ч, а единица времени в модели равна 1 мин, тогда поступление заявок моделируется блоком:

GENERATE 120,FN$XPDIS

Если необходимо моделировать задержку, распределенную пo экспоненциальному закону со средним значением времени 345, то для этого используется блок:

ADVANCE 345,FN$XPDIS

3. Свойство ординарности пуассоновского потока: вероятность поступления двух или более заявок в течение малого временного интервала равна нулю.

Пусть пуассоновский поток моделируется блоком GENERATE 5,FN$XPDIS. Если в результате обращения к функции XPDIS полученное значение меньше чем 1/5, то целая часть произведения числа 5 и значения функции XPDIS равна нулю. Отсюда следует нарушение свойства ординарности пуассоновского потока. Рекомендуется, чтобы операнд А в блоке GENERATE был больше 50.Это легко достигается путем варьирования значения единицы модельного времени.

4. Экспоненциальное распределение не всегда адекватно описывает время обслуживания и поступления требований в систему. Более реалистичным является распределение Эрланга. [4] Для потока Эрланга
k-го порядка c интенсивностью λ математическое ожидание и дисперсия определяются так: 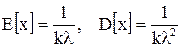. Для моделирования распределения Эрлангаможет использоваться экспоненциальная функция распределения. Для этого достаточно просуммировать kслучайных экспоненциально распределенных величин. C увеличением kраспределение Эрланга будет приближаться к нормальному распределению. Например, поток Эрланга второго порядка со средним значением времени поступления 180 можно задать таким образом:

GENERATE,,,1

SDFG ADVANCE 90,FN$EXPDIS

ADVANCE 90,FN$EXPDIS

SPLIT 1,SDFG

…

TERMINATE 1.

В нулевой момент времени в модель вводится транзакт, который в каждом из двух последующих блоков ADVANCE задерживается на экспоненциально распределенный промежуток времени. Блок SPLIT (подробнее смотреть в [1, 3, 4]) создает копию транзакта и направляет ее на блок c меткой SDFG, исходный транзакт поступает в модель и т. д.

Для того чтобы получить функцию нормального распределения случайной величины Х c математическим ожиданием m_х ≠ 0 и среднеквадратичным отклонением σ_х ≠ 1, необходимо произвести вычисления по формуле: X = m_x + σ_xZ, где Z – случайная величина со стандартной нормальной функцией распределения.

Функция стандартного нормального закона распределения c параметрами m = 0, σ = 1 задается в GPSS двадцатью четырьмя отрезками следующим образом:

NOR FUNCTION RN33,C25

0,-5/.00003,-4/.00135,-3/.00621,-2.5/.02275,-2

.06681,-1.5/.11507,-1.2/.15866,-1/.21186,-.8/.27425,-.6

.34458,-.4/.42074,-.2/.5,0/.57926,.2/.65542,.4

.72575,.6/.78814,.8/.84134,1/.88493,1.2/.93319,1.5

.97725,2/.99379,2.5/.99865,3/.99997,4/1.5

П р и м е р реализации нестандартного нормального закона распределения.

Если случайная величина Х имеет параметры m _x = 60 и σ_x = 10, то в GPSS эта случайная величина моделируется так:

NOR1 FVARIABLE 60+10#FN$NOR

Если необходимо осуществить задержку по этому закону распределения, то применяется блок ADVANCE V$NOR1.

При использовании функции нормального распределения для блоков GENERATE и ADVANCE необходимо обеспечить неотрицательность значений интервалов поступления и задержки. Это можно сделать, используя ограничение m_x ≥ 5σ_x.

В GPSS World в библиотеку процедур включено 24 вероятностных распределения [4].

Пример использования библиотечной процедуры экспоненциального распределения c параметром λ = 0,25 и генератора случайных чисел RN1 для генерации потока транзактов:

GENERATE (Exponential(l,0,(l/0.25)))