Симплекс-метод

Каждое оптимальное решение задач линейного программирования находится в угловой точке области ограничений. При малом количестве переменных и ограничений таких точек немного, и вполне возможно вручную найти координаты всех этих точек и подсчитать в них значение целевой функции.

Однако если в задаче будет 50 переменных и 20 ограничений, то угловых точек, в которых можно считать значение целевой функции, будет порядка 10¹⁴. И если время подсчета значения угловой функции в одной угловой точке будет 0,000001 с, то эту задачу придется решать 2 тыс. лет. Поэтому простой перебор оказывается неэффективным и необходим метод, с помощью которого за конечное число шагов можно прийти к оптимальному решению.

Любое базисное решение, с помощью которого переходят к наиболее оптимальному его варианту, называется опорным решением.

Основные этапы реализации симплекс-метода:

1) указывается способ приведения неканонической задачи к канонической;

2) указывается способ выбора любого опорного решения;

3) устанавливаются критерии оптимальности опорного решения;

4) приводится способ перехода от одного опорного решения к другому, более близкому к оптимальному.

Рассмотрим каноническую задачу линейного программирования для случая, когда значение целевой функции максимизируется:

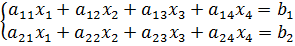
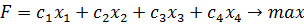
С помощью элементарных преобразований систему можно привести к виду

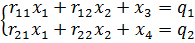
В качестве базисных переменных выберем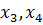

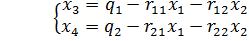
И тогда базисное решение системы имеет вид

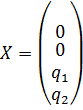
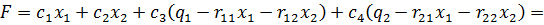
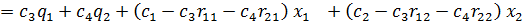
Итак,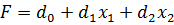

Представим все результаты в виде симплекс-таблицы:

Базис	Цена	План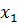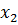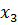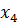
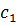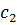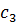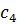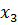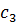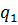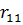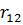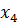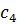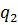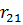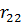F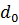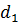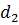

Последняя строка в таблице называется индексной строкой.

По индексной строке симплекс-таблицы можно определить, является ли данное решение оптимальным.

Теорема I. Критерий оптимальности плана.

Если в индексной строке симплекс-таблицы нет положительных элементов, то базисный план, соответствующий этой таблице, оптимален.

Доказательство. Действительно, при любых отрицательных 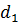и 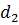и положительных x значение функции F будет меньше .

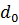Пусть теперь 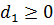, 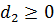и имеется какое-то другое допустимое решение, например:

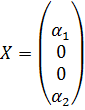
Подставим его в целевую функцию: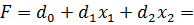

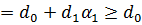
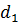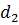Так как нашлось решение, дающее большее значение целевой функции, то при наших предположениях о знаке и решение не является оптимальным. Что и требовалось доказать

Теорема 2. Критерий улучшения опорного плана.

Если в индексной строке имеется хотя бы один положительный элемент и в столбце над ним также имеется хотя бы один положительный элемент, то базисный план может быть улучшен, т.е. можно найти такое базисное решение, при котором значение целевой функции будет больше.

Теорема 3. Критерий отсутствия оптимального плана.

Если в индексной строке симплекс-таблицы имеется положительное число, а в столбце над ним нет ни одного положительного элемента, то задача оптимального плана не имеет.

Аналогичные теоремы можно привести и для случая, когда целевая функция минимизируется.

Теорема 4. Если в индексной строке симплекс-таблицы нет отрицательных элементов, то базисный план оптимален.

Теорема 5. Если в индексной строке симплекс-таблицы имеется хотя бы одно отрицательное число, а в столбце над ним имеется хотя бы одно положительное, то базисный план может быть улучшен.

Теорема 6. Если в индексной строке симплекс-таблицы имеется отрицательное число, а в столбце над ним нет ни одного положительного элемента, то задача оптимального плана не имеет.

Замечание. Переход к новому базису осуществляется с помощью линейных операций над уравнениями системы.

Алгоритм симплекс-метода

1. Привести задачу линейного программирования к канонической, вводя балансовые переменные.

2. Занести данные математической модели в симплекс-таблицу.

2.1. Столбец коэффициентов для базисных переменных имеет вид базисных векторов пространства: одна координата равна 1, а остальные - нулевые.

2.2. Число базисных переменных должно совпадать с числом уравнений в системе ограничений.

2.3. Если в первоначальной таблице нет достаточного количества базисных переменных, над строками выполняются соответствующие элементарные преобразования.

3. Сделать анализ индексной строки:

3.1. Если в индексной строке имеются только отрицательные числа (только положительные) и нули, то данная таблица представляет собой оптимальный план решения задачи на максимум (на минимум): базисным переменным ставится в соответствие число из столбца «План», все остальные переменные обращаются в ноль.

3.2. Если в индексной строке имеется хотя бы одно положительное (отрицательное) число, а в столбце над ним найдется хотя бы один положительный элемент, то базисный план может быть улучшен. Улучшение производится путем перевода основных переменных в базисные с помощью элементарных преобразований над строками расширенной матрицы системы.

3.3. Если в индексной строке имеется хотя бы одно положительное (отрицательное) число, а в столбце над ним нет ни одного положительного элемента, то задача оптимального решения не имеет.

Пример. Для изготовления шкафов и буфетов деревообрабатывающий завод использует древесину четырех видов.

Вид древесины	Запас	Количество древесины на единицу продукции
		Шкаф	Буфет
Прибыль

В таблице указаны запасы древесины, технологические коэффициенты и прибыль от продажи одного буфета и шкафа.

Составить такой план выпуска изделий, при котором прибыль предприятия будет максимальной.

Решение. Пусть х₁ - планируемое к выпуску количество шкафов; х₂ - планируемое к выпуску количество буфетов. Составим математическую модель задачи:

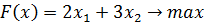
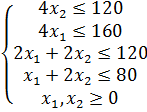
Приведем задачу к канонической, введя балансовые переменные:

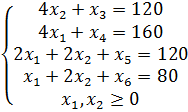
Заполним первую симплекс-таблицу. В базис отправлены балансовые переменные, так как их столбцы представляют собой единичные базисные векторы. В индексной строке имеется два положительных числа и над ними также есть положительные элементы. То есть, данный план может быть улучшен. Выберем наибольшее из положительных чисел в индексной строке и отметим его (это число 3). А в столбце над ним найдем такое число, для которого отношение плановой цифры к нему будет наименьшим (это число 4).

Б	Ц	П		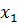		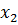		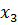		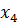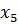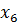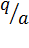д
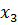									30(min)
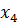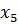										+I*(-1/2)
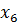										+I*(1/2)
F			3

С помощью элементарных преобразований над строками превратим это число в 1, а остальные числа столбца - в 0 (столбец д). Получим вторую симплекс-таблицу.

Чтобы получить элементы индексной строки, подставим в целевую функцию новый базисный вектор:

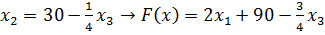. Заполняем и анализируем индексную строку.

Б	Ц	П		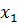		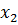		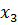		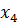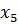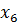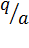д
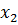					1/4
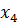									160:4=40
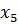					-1/2				60:2=30	+IV*(-4)
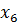					-1/2				20:1=20	+IV*(-4)
F		2		-3/4

Видим, что в индексной строке появилось отрицательное число (-3/4). Но еще остался положительный элемент (2). И в столбце 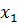над ним также имеются положительные числа. Следовательно, план может быть улучшен. Действуем по тому же алгоритму, что и в первый раз. Получим третью симплекс-таблицу:

Б	Ц	П		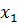		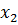		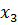	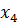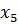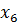д
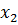					1/4				+III*(1/2)
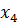									+III*(-4)
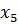					1/2
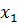					-1/2				+III
F				1/4			-2

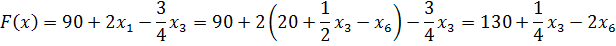
Отмечаем, что в индексной строке имеется положительное число, также и в столбце над ним есть положительные элементы. Преобразуем столбец по известному алгоритму.

Б	Ц	П		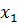		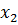		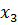	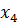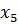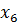д
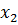							-1/2		+III*(1/2)
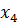							-4		+III*(-4)
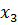								-4
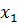								-1	+III
F							-1/2	-1

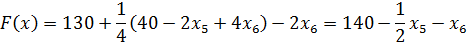
В индексной строке только отрицательные числа и нули. Следовательно, план в данной таблице оптимален. Целевая функция будет принимать значение 140 при значениях переменных базисного столбца, равных соответствующим значениям столбца «План».

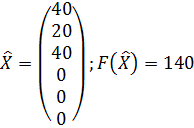
Проведем экономический анализ задачи. Подставим полученные значения переменных в систему ограничений;

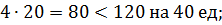
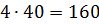
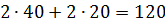
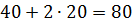
Видим, что при плане изготовления 40 шкафов и 20 буфетов древесина II, III, IV видов будет использована полностью, а 40 единиц древесины I вида останется. Этот остаток и соответствует балансовой переменной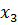

Замечание. Так как в задаче всего две основных переменных, она могла быть решена и графически (см. пример 1 п. 3.1).

Задачи линейного программирования могут иметь не единственное решение.

Теорема (о бесконечном множестве оптимальных планов)

Если в индексной строке симплекс-таблицы, содержащей оптимальный план, имеется хотя бы одна нулевая оценка, соответствующая свободной переменной, то задача линейного программирования имеет бесконечное множество оптимальных планов.