2015-04-20
8647
Нормальным называют распределение вероятностей непрерывной случайной величины X, если дифференциальная функция имеет вид
,
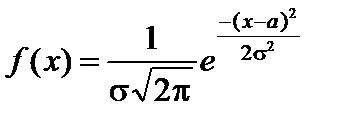где а иs – параметры,
а – математическое ожидание;
s – среднее квадратическое отклонение.
Функция распределения F (x) случайной величины X, распределенной по нормальному закону, имеет вид
.
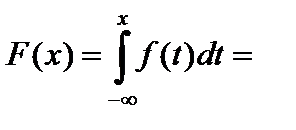
Вероятность того, что X примет значение, принадлежащее интервалу (a; b), вычисляется по формуле
Р (a < X < b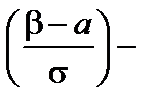) = Ф 
Ф 
,
где Ф(X) =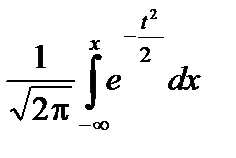 
– функция Лапласса.
Вероятность того, что абсолютная величина отклонения меньше положительного числа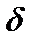 
:
P (|X – a| < d) = 2Ф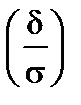 
.
Тест 4.19. Случайная величина X распределена по нормальному закону с параметрами a = 2,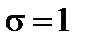 
. Тогда 
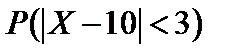равна:
1) 
;
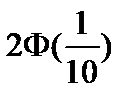2) 
;
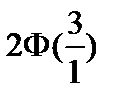3) 
;
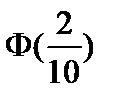4) 
;
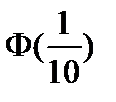5) Ф(1).
В частности, при a = 0 справедливо равенство
.
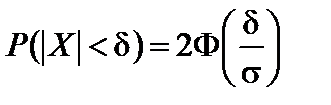«Правило трех сигм». Вероятность того, что абсолютная величина отклонения нормально распределенной случайной величины будет меньше утроенного среднего квадратического отклонения, равна 0,9973:
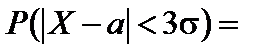2Ф(3)=0,9973.
Свойства функции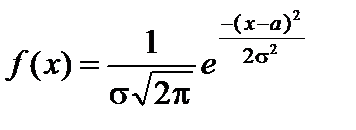 
:
1. Область определения – вся числовая ось.
2. 
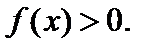
3. 
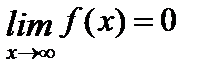, следовательно, ось OX является горизонтальной асимптотой графика функции.
4. Функция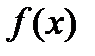 
имеет в точке x=a максимум, равный 
.
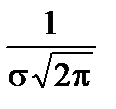5. График функции 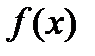симметричен относительно прямой x = a.
6. График функции 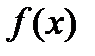в точках 
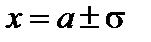имеет перегиб.
На основании перечисленных свойств график функции (нормальная кривая) имеет вид, представленный на рис. 9.
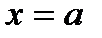
Рис. 9
Тест 4.20. На графике изображена кривая нормального распределения вероятностей (рис. 10).
Рис. 10
Математическое ожидание равно:
1) а = 1;
2) а = 2;
3) а = 3;
4) а = 4;
5) а = 0.
Параметр a характеризует положение нормальной кривой, а параметр s – форму.
На рис. 11 приведено положение нормальной кривой в зависимости от параметра а (если а 1< а 2).
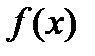
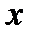
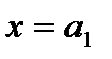
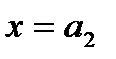
Рис. 11
На рис. 12 приведена форма нормальной кривой в зависимости от параметра s (если 
).
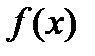
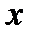
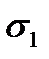
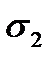
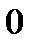
Рис. 12
Тест 4.21. На рисунке рис. 13 изображены три нормальные кривые.
Рис. 13
Меньшему значению а соответствует кривая:
1) 1;
2) 2;
3) 3;
4) положение нормальной кривой не зависит от параметра а;
5) другой ответ.
Тест 4.22. На рис. 14 изображены три нормальные кривые.
| f (x) |
| x |
Рис. 14
Меньшему значению параметра s соответствует нормальная кривая:
1) 1;
2) 2;
3) 3;
4) вид нормальной кривой не зависит от s;
5) другой ответ.
Пример 4.5. Математическое ожидание и среднее квадратическое отклонение нормально распределенной случайной величины Х соответственно равны 20 и 5. какова вероятность того, что в результате испытания случайная величина х примет значение, заключенное в интервале (15;25).
Решение
Воспользуемся формулой
.
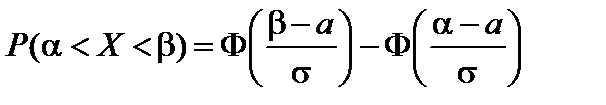Подставив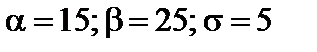 
; a = 20, получим:
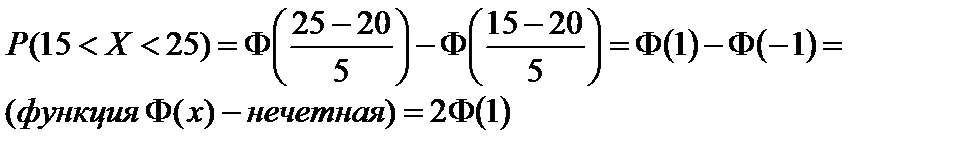
По таблице находим: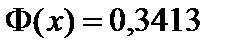 
.
Таким образом,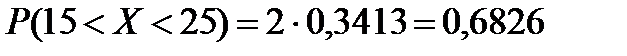 
.
Ответ: 0,6826.
Пример 4.6. Случайная величина Х распределена нормально с математическим ожиданием а = 15. Вероятность попадания х в интервал (15;20) равна 0,2. Чему равна вероятность попадания х в интервал (10;15)?
Решение
Так как график нормальной кривой симметричен относительно прямой x = a = 15,то площади, ограниченные сверху нормальной кривой и снизу интервалами (10;15) и (15;20) равны между собой (рис. 15).
| 0 10 15 20 |
Рис. 15
Поскольку эти площади численно равны вероятностям попадания X в соответствующий интервал, то Р (10 < X < 15) = p(15 < X < 20) = 0,2.
Ответ: 0,2.
Тест 4.23. Нормально распределенная случайная величина х задана дифференциальной функцией
,
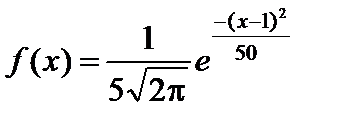Математическое ожидание равно:
1) –1;
2) 0;
3) 1;
4) 5;
5) 
.
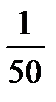Тест 4.24. Нормально распределенная случайная величина х задана дифференциальной функцией
,
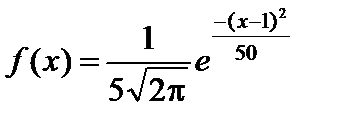Среднее квадратическое отклонение равно:
1) –1;
2) 0;
3) 1;
4) 5;
5) 
.
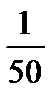Тест 4.25. Случайная величина х распределена нормально с математическим ожиданием а = 8. Вероятность попадания х в интервал (0;4) равна 0,2. вероятность попадания х в интервал (12;16) равна:
1) 0,1;
2) 0;
3)1;
4) 0,4;
5) 0,2.
Тест 4.26. Вероятность попадания в интервал (15;25) нормально распределенной случайной величины х с математическим ожиданием а = 20 и средним квадратическим отклонением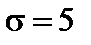 
равна:
1) 
;
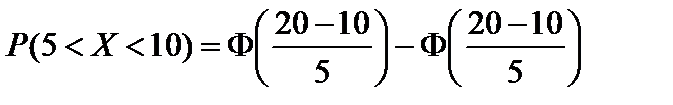2) 
;
3) 
.
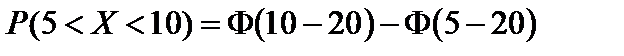Вопросы для самоконтроля
1. Биномиальный закон распределения случайной величин.
2. Закон распределения Пуассона.
3. Равномерный закон распределения.
4. Показательный закон распределения.
5. Нормальный закон распределения.
