Задачей квадратичного программирования называют задачу НЛП, в которой находиться экстремум суммы линейной и квадратичных форм при ограничениях типа линейных неравенств и неотрицательности переменных. Эта задача имеет вид:
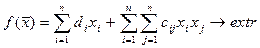 (5.34)
(5.34)
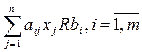 (5.35)
(5.35)
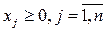
Здесь R – отношение вида 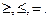
Методика решения задачи квадратичного программирования заключается в следующем:
1. Функция f( 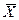 ) проверяется на выпуклость или на вогнутость в зависимости от постановки задачи на максимум или на минимум.
) проверяется на выпуклость или на вогнутость в зависимости от постановки задачи на максимум или на минимум.
2. Записывается функция Лагранжа
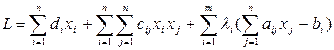
3. Вычисляются частные производные 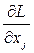 и
и 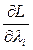
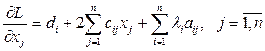
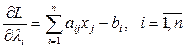
4. Записываются необходимые условия существования седловой точки в
соответствии с типом ограничений (табл. 5.2.). Например, для задачи на максимум и ограничениях типа 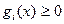 условия Куна-Таккера
условия Куна-Таккера 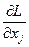 ≤0,
≤0, 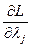 ≥0,
≥0, 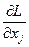 xj= 0,
xj= 0, 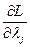 ,
, 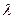 i= 0, xi≥ 0,
i= 0, xi≥ 0, 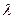 i≥ 0.
i≥ 0.
Примечание: Если типу ограничений соответствуют требования отрицательности множителей Лагранжа, то данные ограничения должны быть преобразованы к типу, для которых 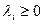 или
или 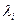 не имеет ограничений. Например, для задачи на максимум с ограничениями типа
не имеет ограничений. Например, для задачи на максимум с ограничениями типа 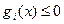 требования к множителям Лагранжа
требования к множителям Лагранжа 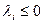 . Тогда ограничения типа
. Тогда ограничения типа 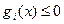 приводятся к виду
приводятся к виду 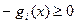 , для которых
, для которых 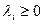 .
.
|
|
|
5. Условия Куна-Таккера записываются в виде равенств путем введения дополнительных переменных.
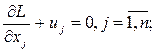 (5.36)
(5.36)
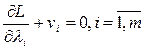
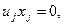
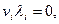
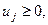
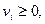
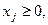
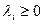 (5.37)
(5.37)
6. Находим координаты седловой точки используя симплекс-метод.
Система (5.36) содержит 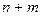 линейных уравнений с
линейных уравнений с 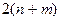 переменными
переменными 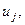
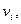
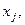
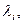 из которых
из которых 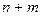 являются свободными и равны нулю. Остальные переменные образуют при этом допустимое базисное решение, если выполняется условие (5.37).
являются свободными и равны нулю. Остальные переменные образуют при этом допустимое базисное решение, если выполняется условие (5.37).
Если в исходной системе (5.36) можно выделить начальное допустимое базисное решение, то его улучшение производят на основании симплекс-метода, аналогичного рассмотренному в задаче линейного программирования. Отличие здесь заключается в том, что при выборе новой базисной переменной каждый раз должны проверяться условия 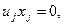
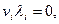 которые означают, что если в базисе имеются
которые означают, что если в базисе имеются 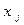 или
или 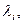 то в него не могут быть введены переменные
то в него не могут быть введены переменные 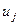 и
и 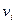 соответственно.
соответственно.
Если в системе (5.36) нельзя сразу выделить начальное допустимое базисное решение, то оно может быть получено введением в систему фиктивных переменных 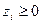 .
.
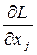 +uj= 0,
+uj= 0,
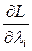 - vi +zi= 0 (5.38)
- vi +zi= 0 (5.38)
В этом случае для улучшения начального допустимого баланса решения используют М-метод (подробнее алгоритм М -метода см. в п.3.5). То есть решают задачу максимизации функции F= 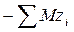 при ограничениях (5.37) и (5.38). Здесь М – сколь угодно большое положительное число. Оптимальное решение может быть получено, если фиктивные переменные перейдут в разряд свободных, то есть будут выведены из базиса в процессе улучшения начального допустимого базисного решения.
при ограничениях (5.37) и (5.38). Здесь М – сколь угодно большое положительное число. Оптимальное решение может быть получено, если фиктивные переменные перейдут в разряд свободных, то есть будут выведены из базиса в процессе улучшения начального допустимого базисного решения.
Пример 5.1 Требуется максимизировать
|
|
|
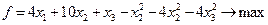 (5.39)
(5.39)
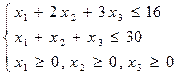 при условиях:
при условиях:
(5.40)
1. Функция f представляет собой сумму линейной функции 4 x1+ 10 x2+x3, которую можно рассматривать как выпуклую и квадратичной –x12- 4 x22- 4 x33. Последняя является отрицательно определенной, следовательно также выпуклой.
2. В соответствии с типом оптимизации (5.39) и видом ограничений (5.40), ограничения, накладываемые на переменные 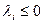 - табличные. Поэтому условия (5.40) должны быть записаны в виде:
- табличные. Поэтому условия (5.40) должны быть записаны в виде:
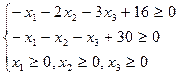
(5.41)
для которых 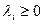 .
.
3. Функция Лагранжа
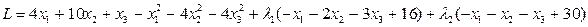
и условие Куна-Таккера (таблица 2):
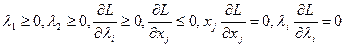
4. Частные производные от функции Лагранжа по переменным 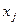 и
и 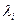
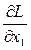 =
= 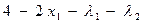
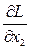 =
= 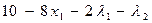
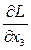 =
= 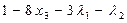
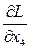 =
= 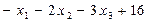
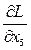 =
= 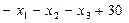
5. Условия Куна-Таккера
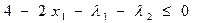
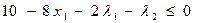
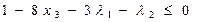
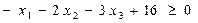
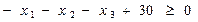 (5.42)
(5.42)
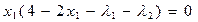
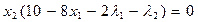
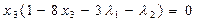
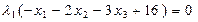
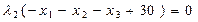
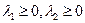
6. Условия (5.42) приводим к каноническому виду (ограничения равенства) путем введения дополнительных переменных u1 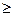 0, u2
0, u2 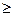 0, u3
0, u3 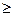 0, v1
0, v1 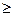 0, v2
0, v2 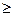 0.
0.
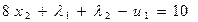
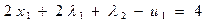
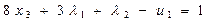
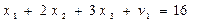 (5.43)
(5.43)
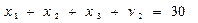
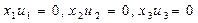
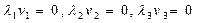
7. Формируем исходный базис путем введения фиктивных переменных 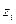 в ограничения (5.43):
в ограничения (5.43):
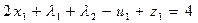
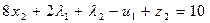
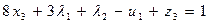
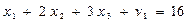 (5.44)
(5.44)
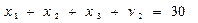
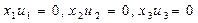
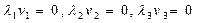
и решаем задачу максимизации функции 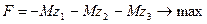 при ограничениях (5.44) симплекс-методом (решение в виде последовательности симплекс-таблиц представлено ниже).
при ограничениях (5.44) симплекс-методом (решение в виде последовательности симплекс-таблиц представлено ниже).
| БП | Cб | В | - м | - м | - м | ||||||||||
| X1 | X2 | X3 | l1 | l2 | U1 | U2 | U3 | V1 | V2 | Z1 | Z2 | Z3 | |||
| Z1 | -м | -1 | |||||||||||||
| Z2 | -м | -1 | |||||||||||||
| Z3 | -м | -1 | |||||||||||||
| V1 | |||||||||||||||
| V2 | |||||||||||||||
| -15 м | 2 м | 8 м | 8 м | 5 м | 3 м | - м | - м | - м |
| БП | Cб | В | -м | -м | -м | ||||||||||
| X1 | X2 | X3 | l1 | l2 | U1 | U2 | U3 | V1 | V2 | Z1 | Z2 | Z3 | |||
| Z1 | - м | -1 | |||||||||||||
| X2 | 1.25 | 0.125 | 0.125 | -0.125 | |||||||||||
| Z3 | - м | 0,12 | |||||||||||||
| V1 | 13.5 | -0.25 | -0.25 | 0.25 | |||||||||||
| V2 | 28.75 | -0.125 | -0.125 | 0.125 | |||||||||||
| -5 м | 2 м | 8 м | 4 м | 2 м | - м | -0.12 м |
| БП | Cб | В | -м | -м | -м | ||||||||||
| X1 | X2 | X3 | l1 | l2 | U1 | U2 | U3 | V1 | V2 | Z1 | Z2 | Z3 | |||
| Z1 | - м | -1 | |||||||||||||
| X2 | 1.25 | 0.125 | 0.125 | -0.125 | |||||||||||
| X3 | 0.125 | 0.375 | 0.125 | -0.016 | |||||||||||
| V1 | 13.125 | -1.375 | -0.625 | 0.25 | 0.047 | ||||||||||
| V2 | 28.625 | -0.5 | -0.25 | 0.125 | 0.016 | ||||||||||
| -4 м | 2 m | m | m | -m |
| БП | Cб | В | -м | -м | -м | ||||||||||
| X1 | X2 | X3 | l1 | l2 | U1 | U2 | U3 | V1 | V2 | Z1 | Z2 | Z3 | |||
| X1 | 0.5 | 0.5 | -0.5 | 0.5 | |||||||||||
| X2 | 1.25 | 0.125 | 0.125 | -0.125 | |||||||||||
| X3 | 0.125 | 0.375 | 0.125 | -0.016 | |||||||||||
| V1 | 11.125 | -1.875 | -1.125 | 0.5 | 0.25 | 0.047 | |||||||||
| V2 | 26.625 | -1 | -0.75 | 0.5 | 0.125 | 0.016 | |||||||||
Оптимальный план 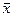 opt= ( 2; 1.25; 0.125; 0; 0; 0; 0; 0; 11.125; 26.625 ).
opt= ( 2; 1.25; 0.125; 0; 0; 0; 0; 0; 11.125; 26.625 ).
Целевая функция Fmax= 4*2+10*1.25+0.125-22-4*0.1252 = 10.3125
Методы, перечисленные ниже, являются методами приближенного вычисления, в отличие от метода множителей Лагранжа, с помощью которого мы получаем точное значение, решая исходную задачу.
 2015-04-30
2015-04-30 4816
4816
