Исследование функций
Дифференциальное исчисление - широко применяемый для экономического анализа
математический аппарат. Базовой задачей экономического анализа является
изучение связей экономических величин, записанных в виде функций. В каком
направлении изменится доход государства при увеличении налогов или при
введении импортных пошлин? Увеличится или уменьшится выручка фирмы при
повышении цены на ее продукцию? В какой пропорции дополнительное оборудование
может заменить выбывающих работников? Для решения подобных задач должны быть
построены функции связи входящих в них переменных, которые затем изучаются с
помощью методов дифференциального исчисления. В экономике очень часто
требуется найти наилучшее или оптимальное значение показателя: наивысшую
производительность труда, максимальную прибыль, максимальный выпуск,
минимальные издержки и т. д. Каждый показатель представляет собой функцию от
одного или нескольких аргументов. Таким образом, нахождение оптимального
|
|
|
значения показателя сводится к нахождению экстремума функции.
По теореме Ферма, если точка является экстремумом функции, то производная в
ней либо не существует, либо равна 0. Тип экстремума можно определить по
одному из достаточных условий экстремума:
1) Пусть функция f(x) дифференцируема в некоторой окрестности точки x0
. Если производная f '(x) при переходе через точку x0 меняет знак с +
на -, то x0 - точка максимума, если с - на +, то x0 -
точка минимума, если не меняет знак, то в этой точке нет экстремума.
2) Пусть функция f(x) дважды дифференцируема в некоторой окрестности точки x
0, причем f '(x0) = 0, f ''(x0) ≠ 0, то в
точке x0 функция f(x0) имеет максимум, если f ''(x0
) < 0 и минимум, если f ''(x0) > 0.
Кроме того, вторая производная характеризует выпуклость функции (график
функции называется выпуклым вверх [вниз] на интервале (a, b), если он на этом
интервале расположен не выше [не ниже] любой своей касательной).
Пример: выбрать оптимальный объем производства фирмой, функция прибыли
которой может быть смоделирована зависимостью:
π(q) = R(q) - C(q) = q2 - 8q + 10
Решение:
π'(q) = R'(q) - C'(q) = 2q - 8 = 0 → qextr = 4
При q < qextr = 4 → π'(q) < 0 и прибыль убывает
При q > qextr = 4 → π'(q) > 0 и прибыль возрастает
При q = 4 прибыль принимает минимальное значение.
Каким же будет оптимальный объем выпуска для фирмы? Если фирма не может
производить за рассматриваемый период больше 8 единиц продукции (p(q = 8) =
p(q = 0) = 10), то оптимальным решением будет вообще ничего не производить, а
получать доход от сдачи в аренду помещений и / или оборудования. Если же
фирма способна производить больше 8 единиц, то оптимальным для фирмы будет
|
|
|
выпуск на пределе своих производственных мощностей.
Эластичность спроса
Эластичностью функции f(x) в точке x0 называют предел
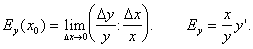
Спрос - это количество товара, востребованное покупателем. Ценовая эластичность
спроса ED - это величина, характеризующая то, как спрос реагирует на
изменение цены. Если │ED│>1, то спрос называется
эластичным, если │ED│<1, то неэластичным. В случае E
D=0 спрос называется совершенно неэластичным, т. е. изменение цены не
приводит ни к какому изменению спроса. Напротив, если самое малое снижение цены
побуждает покупателя увеличить покупки от 0 до предела своих возможностей,
говорят, что спрос является совершенно эластичным. В зависимости от текущей
эластичности спроса, предприниматель принимает решения о снижении или повышении
цен на продукцию.
Предельный анализ
Важный раздел методов дифференциального исчисления, используемых в экономике
- методы предельного анализа, т. е. совокупность приемов исследования
изменяющихся величин затрат или результатов при изменениях объемов
производства, потребления и т. п. на основе анализа их предельных значений.
Предельный показатель (показатели) функции - это ее производная (в случае
функции одной переменной) или частные производные (в случае функции
нескольких переменных)
В экономике часто используются средние величины: средняя производительность
труда, средние издержки, средний доход, средняя прибыль и т. д. Но часто
требуется узнать, на какую величину вырастет результат, если будут увеличены
затраты или наоборот, насколько уменьшится результат, если затраты
сократятся. С помощью средних величин ответ на этот вопрос получить
невозможно. В подобных задачах требуется определить предел отношения
приростов результата и затрат, т. е. найти предельный эффект. Следовательно,
для их решения необходимо применение методов дифференциального исчисление.
ТЕМА 12: Решение дифференциальных уравнений. Индивидуальное задание №1. Самостоятельная работа.
ПРАКТИЧЕСКАЯ ЧАСТЬ
Контрольные вопросы:
1. Что называется дифференциальным уравнением 1-го порядка?
__________________________________________________________
__________________________________________________________
__________________________________________________________
__________________________________________________________
2. Написать общий вид дифференциального уравнения 1-го порядка с разделяющимися переменными.______________________________
__________________________________________________________
3. Какая замена неизвестной функции позволяет свести однородное дифференциальное уравнение 1-го порядка к уравнению с разделяющимися переменными?______________________________
__________________________________________________________
__________________________________________________________
__________________________________________________________
__________________________________________________________
__________________________________________________________
__________________________________________________________
4. Написать общий вид однородного линейного дифференциального уравнения 2-го порядка с постоянными коэффициентами. Что называется его характеристическим уравнением?______________
________________________________________________________
________________________________________________________
________________________________________________________
________________________________________________________
________________________________________________________
5. Что значит решить задачу Коши?____________________________
________________________________________________________
_________________________________________________________
6. Какие виды решений имеет дифференциальное уравнение?_____
_________________________________________________________
_________________________________________________________
_________________________________________________________
_________________________________________________________
Тема: Системы линейных уравнений и методы их решения.
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
Система линейных алгебраических уравнений имеет вид:
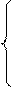 а11х1 + а12х2 + а13х3 = в1
а11х1 + а12х2 + а13х3 = в1
а21х1 + а22х2 + а23х3 = в2
а31х1 + а32х2 + а33х3 = в3
Это система трех уравнений с тремя неизвестными х1, х2, х3. Вещественные числа аij (i = 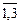 , j =
, j = 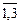 ) называются коэффициентами системы. в1, в2, в3 – свободные члены. Если хотя бы одно из чисел в1, в2, в3, отлично от нуля, система называется неоднородной. Если все свободные члены равны нулю, то система имеет вид:
) называются коэффициентами системы. в1, в2, в3 – свободные члены. Если хотя бы одно из чисел в1, в2, в3, отлично от нуля, система называется неоднородной. Если все свободные члены равны нулю, то система имеет вид:
|
|
|
 а11х1 + а12х2 + а13х3 = 0
а11х1 + а12х2 + а13х3 = 0
а21х1 + а22х2 + а23х3 = 0
а31х1 + а32х2 + а33х3 = 0 и называется однородной.
Системы решаются одним из следующих способов: 1) методом Гаусса, или методом исключения неизвестных; 2) по формулам Крамера;
3) матричным методом.
Метод Гаусса
Исторически первым, наиболее распространенным методом решения систем линейных уравнений является метод Гаусса, или метод последовательного исключения неизвестных. Сущность этого метода состоит в том, что посредством последовательных исключений неизвестных данная система превращается в ступенчатую (в частности, треугольную) систему, равносильную данной. При практическом решении системы линейных уравнений методом Гаусса удобнее приводить к ступенчатому виду не саму систему уравнений, а расширенную матрицу этой системы, выполняя элементарные преобразования над ее строками. Последовательно получающиеся в ходе преобразования матрицы обычно соединяют знаком эквивалентности.
Пример 1. Решить систему уравнений методом Гаусса:
 x + y - 3z = 2,
x + y - 3z = 2,
3x - 2y + z = - 1,
2x + y - 2z = 0.
Решение. Выпишем расширенную матрицу данной системы
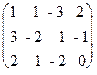
и произведем следующие элементарные преобразования над ее строками:
а) из ее второй и третьей строк вычтем первую, умноженную соответственно на 3 и 2:
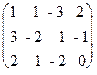 ~
~ 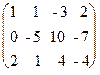 ;
;
б) третью строку умножим на (-5) и прибавим к ней вторую:
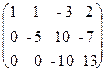 .
.
В результате всех этих преобразований данная система приводится к треугольному виду:
 x + y - 3z = 2,
x + y - 3z = 2,
-5y + 10z = -7,
- 10z = 13.
Из последнего уравнения находим z = -1,3. Подставляя это значение во второе уравнение, имеем y = -1,2. Далее из первого уравнения получим
x = - 0,7.
По формуле Крамера решаются только неоднородные системы.
Определитель системы Δ называется определитель, составленный из коэффициентов системы:
Δ = 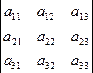
Если определитель системы Δ не равен 0, то система имеет единственное решение, которое находится по формулам:
|
|
|
Х1 = Δх1/ Δ; х2== Δх2/ Δ; х3== Δх3/ Δ; где
Δх1= 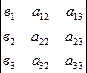 ; Δх2=
; Δх2= 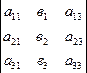 ; Δх3=
; Δх3= 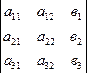 .
.
Если определитель системы = Δ равен нулю, и хотя бы один из определителей ∆х1=∆х2=∆х3 отличен от нуля, то система несовместна.
Если определитель системы ∆=0, и ∆х1=∆х2=∆х3=0, то система имеет бесконечное множество решений. (неопределенная система).
Пример 2. Решить систему уравнений:
 Х + 2у – z = 1
Х + 2у – z = 1
-3х + у = 2z = 0
х + 4у + 3z = 2
1) Вычислим определитель системы ∆ = 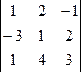 = 1*1*3+2*2*1+(-1)*4*(-3) – (1*1*(-1)+4*2*1+3*2*(-3))=3+4+12 – (-1 + 8 – 18) = 19+11 = 30.
= 1*1*3+2*2*1+(-1)*4*(-3) – (1*1*(-1)+4*2*1+3*2*(-3))=3+4+12 – (-1 + 8 – 18) = 19+11 = 30.
Система имеет единственное решение, т.к. определитель ∆ = 30 ≠ 0.
2) Вычислим определители ∆х, ∆у, ∆z.
∆х = 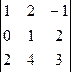 = 5; ∆у =
= 5; ∆у = 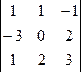 = 13; ∆z =
= 13; ∆z = 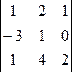 = 1.
= 1.
3) По формулам Крамера находим решение системы:
Х = ∆х/∆ = 5/30 = 1/6; у = ∆у/∆ = 13/30; z = ∆z/∆ = 1/30;
Ответ: решение системы (1/6; 13/30; 1/30).
По формулам Крамера можно решить систему n линейных уравнений с n неизвестными.
Пример 3 Решить систему уравнений двумя методами.
 х - у+z=1
х - у+z=1
х + у – z=2
5х + у – z=7
1) Составим и вычислим определитель системы ∆=  = 0.
= 0.
2) Вычислим определители ∆х, ∆у, ∆z.
∆х = 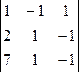 = 0, ∆у =
= 0, ∆у = 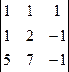 = -2
= -2
Т.к. определитель ∆у= -2 ≠ 0, мы делаем заключение: Система несовместна, т.е. она не имеет решения.
ПРАКТИЧЕСКАЯ ЧАСТЬ
ТЕСТЫ
1. Решить систему линейных алгебраических уравнений 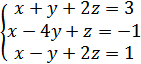
А) (5;2;-4)
Б) (2;-4;1)
В) (4;1;-1)
Г) (-2;-4;2)
2. Решить систему линейных алгебраических уравнений 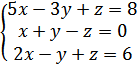
А) (5;5;2)
Б) (2;1;4)
В) (4;1;2)
Г) (2;2;4)
3. Решить систему уравнений 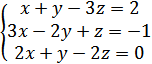
А) (1;05;2)
Б) (-0,7;-1,2;-1,3)
В) (7;10;3)
Г) (2;3;-5)
4. Решить систему уравнений 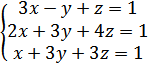
А) (1;2;4)
Б) (2;-3;1)
В) (5;-3;3)
Г) (1;1;-1)
5. Решить систему уравнений 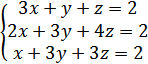
А) (0,5;1;-0,5)
Б) (5;1;-5)
В) (2;-4;7)
Г) (1,2;-1,2;1)
Тема: Решение систем линейных уравнений по правилу Крамера
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
По формуле Крамера решаются только неоднородные системы.
Определитель системы Δ называется определитель, составленный из коэффициентов системы:
Δ = 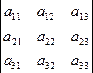
Если определитель системы Δ не равен 0, то система имеет единственное решение, которое находится по формулам:
Х1 = Δх1/ Δ; х2== Δх2/ Δ; х3== Δх3/ Δ; где
Δх1= 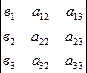 ; Δх2=
; Δх2= 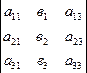 ; Δх3=
; Δх3= 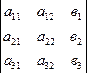 .
.
Если определитель системы = Δ равен нулю, и хотя бы один из определителей ∆х1=∆х2=∆х3 отличен от нуля, то система несовместна.
Если определитель системы ∆=0, и ∆х1=∆х2=∆х3=0, то система имеет бесконечное множество решений. (неопределенная система).
ПРАКТИЧЕСКАЯ ЧАСТЬ
ТЕСТЫ
1. Решить систему уравнений 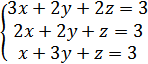
А) (5;1;-2)
Б) (2;-1;1)
В) (3;-2;-1)
Г) (1;1;-1)
2. Решить систему уравнений 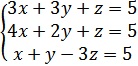
А) (3;1;1)
Б) (2;-3;1)
В) (1;1;-1)
Г) (-1;1;-1)
3. Решить систему уравнений 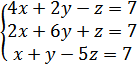
А) (6;-1;2)
Б) (3;-3;1)
В) (-2;1;-1)
Г) (1;1;-1)
4. Решить систему уравнений 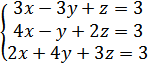
А) (3;-2;2)
Б) (-1;-1;3)
В) (2;-1;3)
Г) (1;-1;1)
5..Решить систему уравнений 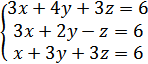
А) (5;-4;3)
Б) (-3;6;-3)
В) (-2;3;-4)
Г) (-7;2;5)
Тема: Решение систем линейных уравнений.
ПРАКТИЧСКАЯ ЧАСТЬ
Тест
1. Каким методом нельзя решить СЛАУ:
А) метод Лобачевского;
Б) метод Крамера;
В) матричным методом.
2. Метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого вида, из которого последовательно, начиная с последних переменных, находятся все остальные переменные – это метод …
А) Крамера;
Б) Гаусса;
В) Зейделя.
3. По формуле Крамера, если определитель системы Δ не равен 0, то система:
А) не имеет решения;
Б) имеет единственное ршение;
В) имеет множество решений.
4. Правельным ответом САЛУ является 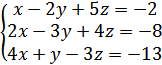
А) (-2;3;-1)
Б) (7;-3;2)
В) (-3;2;1)
5. Что является ответом СЛАУ 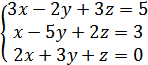
А) (3;-1;2)
Б) (-5;2;-8)
В) любое число
6. Решением является 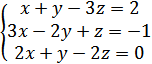
А) (2;-5;1)
Б) (-0,7;-1,2;-1,3)
В) (7;-2;13)
7. Решив СЛАУ методом Гаусса вы получили ответ 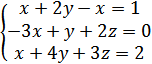
А) (0,15;0,44;0,03)
Б) (-0,3;1,2;0,15)
В) (7;0,5;-2)
8. Если решать СЛАУ методом Крамера 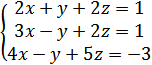 ответ будет
ответ будет
А) (2;1;-2)
Б) (4;-1;2)
В) ответа нет
9. Найти сумму x+y+z, где (x;y;z) решение системы 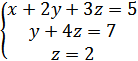
А) -2
Б) 0
В) -1
10. Решите СЛАУ 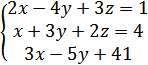
А) (15;2;7)
Б) (0,7;-0,2;1,2)
В) (-1,5;0,5;2)
Тема: Системы линейных неравенств, графический способ их решения.
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
Линейные неравенства имеют особо важное значение для экономистов, т.к именно при помощи линейных неравенств можно смоделировать производственные процессы и найти наиболее выгодные планы производства, транспортировки, размещения ресурсов и т. д. Графический метод заключается в построении множества допустимых решений ЗЛП, и нахождении в данном множестве точки, соответствующей max/min целевой функции.
Система ограничений такой задачи состоит из неравенств от двух переменных:
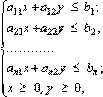
и целевая функция имеет вид F = C 1 x + C 2 y, которую необходимо максимизировать.
Ответим на вопрос: какие пары чисел (x; y) являются решениями системы неравенств, т. е. удовлетворяют каждому из неравенств одновременно?
Предварительно необходимо понять, что является решением одного линейного неравенства с двумя неизвестными.
Решить линейное неравенство с двумя неизвестными – это значит определить все пары значений неизвестных, при которых неравенство выполняется.
Например, неравенству 3 x – 5 y ≥ 42 удовлетворяют пары (x, y): (100, 2); (3, –10) и т. д. Задача состоит в нахождении всех таких пар.
Рассмотрим два неравенства: ax + by ≤ c, ax + by ≥ c. Прямая ax + by = c делит плоскость на две полуплоскости так, что координаты точек одной из них удовлетворяют неравенству ax + by > c, а другой неравенству ax + + by < c.
Действительно, возьмем точку с координатой x = x 0; тогда точка, лежащая на прямой и имеющая абсциссу x 0, имеет ординату
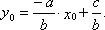
Итак,
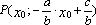
Пусть для определенности a < 0, b >0, c >0. Все точки с абсциссой x 0, лежащие выше P (например, точка М), имеют yM > y 0, а все точки, лежащие ниже точки P, с абсциссой x 0, имеют yN < y 0. Поскольку x 0 –произвольная точка, то всегда с одной стороны от прямой будут находиться точки, для которых ax + by > c, образующие полуплоскость, а с другой стороны – точки, для которых ax + by < c.
Знак неравенства в полуплоскости зависит от чисел a, b, c.
Отсюда вытекает следующий способ графического решения систем линейных неравенств от двух переменных. Для решения системы необходимо:
1. Для каждого неравенства выписать уравнение, соответствующее данному неравенству.
2. Построить прямые, являющиеся графиками функций, задаваемых уравнениями.
3. Для каждой прямой определить полуплоскость, которая задается неравенством. Для этого взять произвольную точку, не лежащую на прямой, подставить ее координаты в неравенство. если неравенство верное, то полуплоскость, содержащая выбранную точку, и является решением исходного неравенства. Если неравенство неверное, то полуплоскость по другую сторону прямой является множеством решений данного неравенства.
4. Чтобы решить систему неравенств, необходимо найти область пересечения всех полуплоскостей, являющихся решением каждого неравенства системы.
Эта область может оказаться пустой, тогда система неравенств не имеет решений, несовместна. В противном случае говорят, что система совместна.
Решений может быть конечное число и бесконечное множество. Область может представлять собой замкнутый многоугольник или же быть неограниченной.
Рассмотрим три соответствующих примера.
Пример 1. Решить графически систему:
x + y – 1 ≤ 0;
–2 x – 2 y + 5 ≤ 0.
Решение:
– рассмотрим уравнения x + y –1 = 0 и –2 x – 2 y + 5 = 0, соответствующие неравенствам;
– построим прямые, задающиеся этими уравнениями.
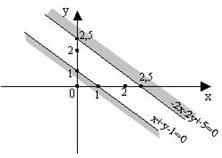
Определим полуплоскости, задаваемые неравенствами. Возьмем произвольную точку, пусть (0; 0). Рассмотрим x + y– 1  0, подставим точку (0; 0): 0 + 0 – 1 ≤ 0. значит, в той полуплоскости, где лежит точка (0; 0), x + y – 1 ≤ 0, т.е. полуплоскость, лежащая ниже прямой, является решением первого неравенства. Подставив эту точку (0; 0), во второе, получим: –2 ∙ 0 – 2 ∙ 0 + 5 ≤ 0, т.е. в полуплоскости, где лежит точка (0; 0), –2 x – 2 y + 5≥ 0, а нас спрашивали, где –2 x – 2 y + 5 ≤ 0, следовательно, в другой полуплоскости – в той, что выше прямой.
0, подставим точку (0; 0): 0 + 0 – 1 ≤ 0. значит, в той полуплоскости, где лежит точка (0; 0), x + y – 1 ≤ 0, т.е. полуплоскость, лежащая ниже прямой, является решением первого неравенства. Подставив эту точку (0; 0), во второе, получим: –2 ∙ 0 – 2 ∙ 0 + 5 ≤ 0, т.е. в полуплоскости, где лежит точка (0; 0), –2 x – 2 y + 5≥ 0, а нас спрашивали, где –2 x – 2 y + 5 ≤ 0, следовательно, в другой полуплоскости – в той, что выше прямой.
Найдем пересечение этих двух полуплоскостей. Прямые параллельны, поэтому плоскости нигде не пересекаются, значит система данных неравенств решений не имеет, несовместна.
Пример 2. Найти графически решения системы неравенств:
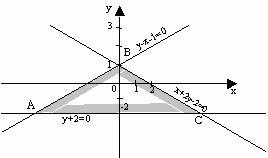
Рисунок 3
1. Выпишем уравнения, соответствующие неравенствам, и построим прямые.
x + 2 y – 2 = 0
| x | ||
| y |
y – x – 1 = 0
| x | ||
| y |
y + 2 = 0;
y = –2.
2. Выбрав точку (0; 0), определим знаки неравенств в полуплоскостях:
0 + 2 ∙ 0 – 2 ≤ 0, т.е. x + 2 y – 2 ≤ 0 в полуплоскости ниже прямой;
0 – 0 – 1 ≤ 0, т.е. y – x – 1 ≤ 0 в полуплоскости ниже прямой;
0 + 2 =2 ≥ 0, т.е. y + 2 ≥ 0 в полуплоскости выше прямой.
3. Пересечением этих трех полуплоскостей будет являться область, являющаяся треугольником. Нетрудно найти вершины области, как точки пересечения соответствующих прямых
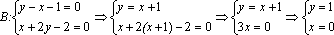
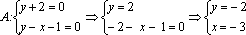
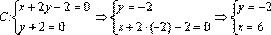
Таким образом, А (–3; –2), В (0; 1), С (6; –2).
Рассмотрим еще один пример, в котором получившаяся область решения системы неограничена.
Пример 3. Решить графически систему
Выпишем уравнения, соответствующие неравенствам, и построим прямые.
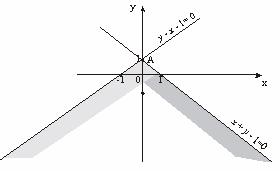
Рисунок 4
x + y – 1 = 0
| x | ||
| y |
y – x – 1 = 0
| x | –1 | |
| y |
Определим знаки в полуплоскостях. Выберем точку (0; 0):
0 – 0 – 1 ≤ 0, т.е. y – x – 1 ≤ 0 ниже прямой;
0 + 0 – 1 ≤ 0, т.е. x + y – 1 ≤ 0 ниже прямой.
Пересечением двух полуплоскостей является угол с вершиной в точке А (0;1). Эта неограниченная область является решением исходной системы неравенств.
Тема: Вычисление наибольшего и наименьшего значения линейной функции на выпуклом многоугольнике.
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
Общей задачей линейного программирования называется задача, которая состоит в определении максимального (минимального) значения функции
Функция называется целевой функцией (или линейной формой) задачи.
Ограничение-неравенство исходной задачи линейного программирования, имеющее вид “ 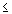 ”, можно преобразовать в ограничение-равенство добавлением к его левой части дополнительной неотрицательной переменной, а ограничение-неравенство вида “
”, можно преобразовать в ограничение-равенство добавлением к его левой части дополнительной неотрицательной переменной, а ограничение-неравенство вида “ 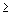 ” – в ограничение-равенство вычитанием из его левой части дополнительной неотрицательной переменной. Таким образом, ограничение-неравенство
” – в ограничение-равенство вычитанием из его левой части дополнительной неотрицательной переменной. Таким образом, ограничение-неравенство
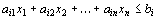
В то же время каждое уравнение системы ограничений
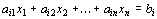
можно записать в виде неравенств:
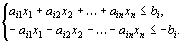
Число вводимых дополнительных неотрицательных переменных при преобразовании ограничений-неравенств в ограничения-равенства равно числу преобразуемых неравенств.
Вводимые дополнительные переменные имеют вполне определенный экономический смысл. Так, если в ограничениях исходной задачи линейного программирования отражается расход и наличие производственных ресурсов, то числовое значение дополнительной переменной в плане задачи, записанной в форме основной, равно объему неиспользуемого соответствующего ресурса.
Отметим, наконец, что если переменная 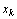 , не подчинена условию неотрицательности, то ее следует заменить двумя неотрицательными переменными
, не подчинена условию неотрицательности, то ее следует заменить двумя неотрицательными переменными 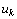 и
и 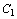 , приняв
, приняв 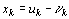 .
.
Пример 1. Записать в форме основной задачи линейного программирования следующую задачу: найти максимум функции 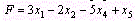 при условиях
при условиях
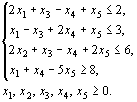
Решение. В данной задаче требуется найти максимум функции, а система ограничений содержит четыре неравенства. Следовательно, чтобы записать ее в форме основной задачи, нужно перейти от ограничений-неравенств к ограничениям-равенствам. Так как число неравенств, входящих в систему ограничений задачи, равно четырем, то этот переход может быть осуществлен введением четырех дополнительных неотрицательных переменных. При этом к левым частям каждого из неравенств вида“ 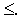 “ соответствующая дополнительная переменная прибавляется, а из левых частей каждого из неравенств вида “
“ соответствующая дополнительная переменная прибавляется, а из левых частей каждого из неравенств вида “ 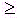 ” вычитается. В результате ограничения принимают вид уравнений:
” вычитается. В результате ограничения принимают вид уравнений:
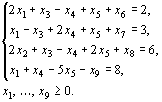
Следовательно, данная задача может быть записана в форме основной задачи таким образом: максимизировать функцию 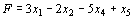 при условиях
при условиях
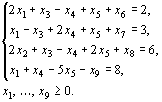
 2015-05-05
2015-05-05 3276
3276
