Следствия из аксиом линейного пространства

1°. Нулевой (нейтральный) элемент пространства единственен.

◀ Пусть имеется два нулевых элемента q₁ и q₂. Тогда

1. x ⊕ q₁ = x (Положим в этом равенстве x = q₂). Получим q₂ ⊕ q₁ = q_2.

2. x ⊕ q₂ = x (Аналогично положим x = q₁). Получим q₁ ⊕ q₂ = q₁. У равенств полученных в первой и во второй строках левые части равны, следовательно, правые части также равны Þ q₂ = q₁. ▶

2°. Противоположный вектор к вектору x единственен.

◀ Пусть y и z - элементы противоположные x. Тогда

y = y ⊕q = y ⊕ (x ⊕ z) = (y ⊕ x)⊕ z = q ⊕ z = z; Þ y = z. ▶

3°. 0⊙ x = q.

◀ 0⊙ x ⊕ y = 0⊙ x ⊕ y ⊕ q = 0⊙ x ⊕ y ⊕ x ⊕(– x) = (0 + 1)⊙ x ⊕(– x) ⊕ y =

= x ⊕ (– x)⊕ y = q ⊕ y = y, т.е. 0⊙ x ⊕ y = y Þ 0⊙ x = q. ▶

4°. " x (–1)⊙ x –его противоположный элемент.

◀ x ⊕(–1)⊙ x = 1⊙ x ⊕(–1)⊙ x = (1 – 1)⊙ x = 0⊙ x = q. ▶

5°. a⊙q = q.

◀ a⊙q = a⊙(q ⊕ q) = a⊙q ⊕ a⊙q. Прибавим к левой и правой части элемент противоположный a⊙q, т.е. (– a⊙q). Получим в левой части a⊙q ⊕(– a⊙q) = q, а в правой части a⊙q ⊕ a⊙q ⊕(– a⊙q) = a⊙q ⊕ q = a⊙q. Следовательно a⊙q = q. ▶

6°. Если a ⊙ х = q, тоa = 0 или x = q.

◀ Если a = 0, то равенство выполнено (см. 3°). Если a ¹ 0, то

x = 1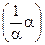⊙ x= ⊙ x = 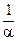⊙(a⊙ x) = 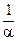⊙q = q,т.е. x = q. ▶

Замечание: В дальнейшем, если это не будет приводить к недоразумениям, будем пользоваться знаком + вместо ⊕, а знак ⊙ будем опускать.