Операции над диграфами

3.2.1. Простейшие операции

Простейшими операциями над диграфами являются:

· Добавление вершины: D+V_n+1;

· Удаление вершины: D-V_i (вершина удаляется вместе с инцидентными к ней и от нее дугами);

· Добавление дуги: D+{V_i,V_j};

· Удаление дуги: D-{V_i,V_j};

· Изменение направления дуги: {V_i,Vj}Þ{V_j,V_i};

· Замена дуги на ребро.

Определение

3.2.1. Унарные операции

Диграф Н(W,F) является поддиграфом диграфа D=(V,А), если WÍV и FÍА (т.е. все вершины и дуги которого являются вершинами и дугами диграфа).

Если множество вершин поддиграфа равно множеству вершин диграфа, то такой поддиграф называется каркасным.

Если W является подмножеством вершин диграфа D=(V,A), то подграфом, индуцированным множеством W, будет подграф с вершинами W и всеми дугами диграфа D между этими вершинами.

Диграф, полученный из диграфа заменой дуг на ребра, называется неографом основания.

Обратный диграф D^-1(V,E^-1) – это диграф, у которого множества вершин совпадает с множеством вершин исходного диграфа, а дуги имеют обратную ориентацию.

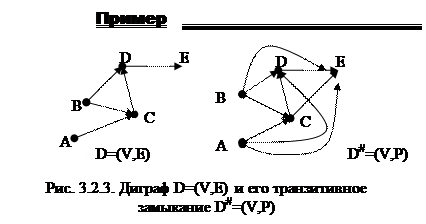
Транзитивным замыканием диграфа D=(V,E) называется такой диграф D^#=(V,P), который:

· имеет те же вершины, что и диграф D;

· если D имеет направленный путь от вершины u к вершине v (u¹v), то диграф D^# имеет дугу от u к v

Операция построения реберного диграфа L(D)=(U,F) диграфа D=(V,A) состоит в следующем:

· каждой вершине u U реберного диграфа L(D) сопоставлена дуга диграфа D;

· вершины L(D) соединены дугой, если для двух дуг диграфа{x₁,y₁},{x₂,y₂} A выполняется условие y₁=x₂ (т.е. голова дуги {x₁,y₁} совпадает с хвостом дуги {x₂,y₂}).

При заданном диграфе D=(V,A) имеется рекурсивное определение реберных диграфов порядка два, три и более:

L(L(D))=L²(D), L(L²(D)), …

	Определение

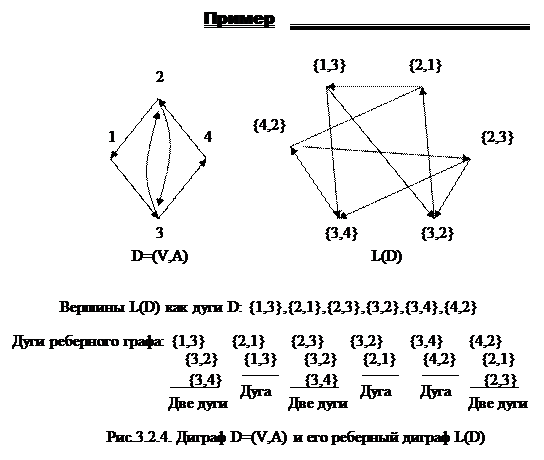Полным подразбитием диграфа D=(V,A) является диграф D^’=(V,A^’), получаемый из D заменой каждой дуги двумя дугами с новой вершиной между ними (новые дуги имеют то же направление, что и заменяемая дуга).

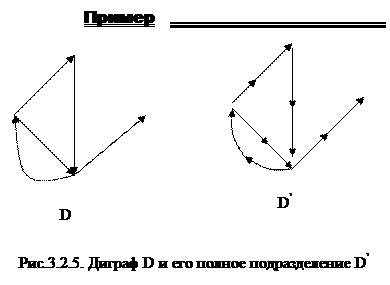k-ой степенью диграфа D=(V,A) является диграф, с тем же множеством вершин и дугой между двумя вершинами тогда и только тогда, когда в диграфе D между ними существует направленный путь длины точно k.

Определения

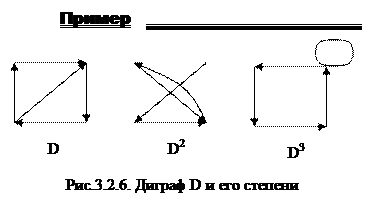2.2.3. Бинарные операции

Объединением (disjoint union) диграфов D₁=(V₁,A₁) и D₂=(V₂,A₂) является диграф (или иной вид графа) D=(V,A), V=V₁ 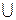V₂, A=A₁ 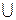A₂.

Произведение диграфов (digraph product) D₁=(V₁,A₁) и D₂=(V₂,A₂) - диграф, у которого:

· множество вершин равно V₁ 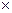V₂ (т.е. множество пар, где первый элемент взят из множества вершин V₁. а второй – из множества V₂);

· смежность дуг к и от полученной вершины определяется неоднозначно.

Некоторые из произведений двух диграфов определяются следующим образом:

Конъюнкцией (conjunction) D₁ 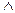D₂ двух диграфов D₁=(V₁,A₁) и D₂=(V₂,A₂) является диграф с множеством вершин V₁ 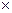V₂, у которого имеется дуга из вершины (u₁,u₂) к вершине (v_1,v₂) тогда и только тогда, когда имеются дуга из вершины u₁ вершину v₁ диграфа D₁ и дуга из вершины u₂ в вершину v₂ диграфа D₂ .

Круговым произведением (wreath product) D₁¦D₂ двух диграфов D₁=(V₁,A₁) и D₂=(V₂,A₂) является диграф с множеством вершин V₁ 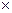V₂, у которого между парами вершин имеется дуга, если выполняются условия:

{(x₁,y₁),(x₁,y₂): {x₁,y₂} является дугой диграфа D₁}

и

{(x₁,y₁),(x₁,y₂): {x₂,y₂} является дугой диграфа D₂}.

Декартово произведение (Cartesian product) D₁ 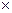D₂ двух диграфов D₁=(V₁,A₁) и D₂=(V₂,A₂) является диграф с множеством вершин V₁ 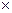V₂, у которого дуга начинает D₁ D₁ся на вершине (u₁,u₂) и заканчивается на вершине (v₁,v₂), если {u₁,v₁} A₁, {u₂,v₂} A₂ и u₁=v₁, u₂=v₂.

Определение

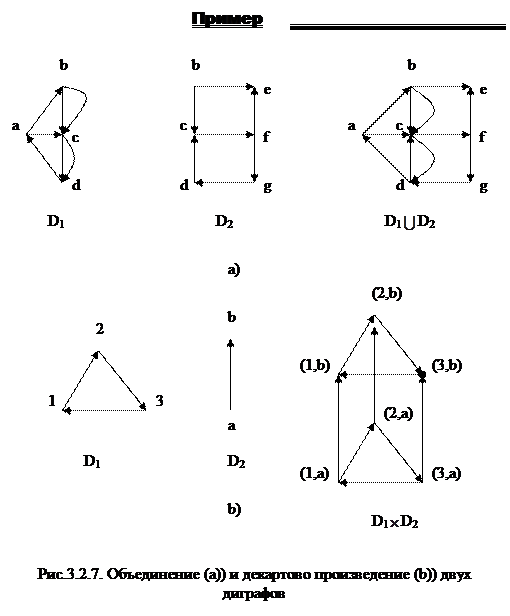3.3. Некоторые виды диграфов

Полные диграфы – это диграфы, у которых каждая пара вершин соединенадвумя взаимно направленными дугами.

Диграф D=(V,A) назывется регулярным степени (r,s), если каждая его вершина имеет полустепень исхода r и полустепень захода s.

Регулярный степени (d,d) диграф является d-регулярным диграфом, а величина d – степенью диграфа.

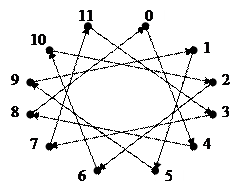Турниром T=(V,A) называется диграф, у которого для каждой пары вершин u,v V, u v, имеется одна дуга между ними (либо {u,v}, либо {v,u}).

k-дольным турниром будет диграф T=(V,A), такой, что множество его вершин V может быть разбито на k разделенных частей P₁,P₂,…,P_k, а дуга в Т существует между двумя вершинами u P_i и v P_j тогда и только тогда, когда i 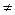j. При k=2 турнир называется двудольным.

3.4. Изоморфизм диграфа

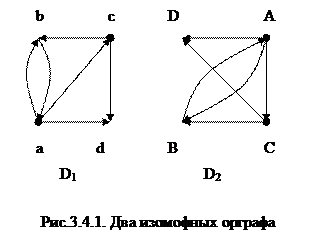
Два диграфа D и H являются изоморфными, если диграф H может быть получен переименованием всех вершин диграфа D, при этом имеется взаимно однозначное соответствие между дугами диграфов D и H (соответствия по числу, инцидентности и направлению).

Формально, два диграфа D₁=(V_1,V₂) и D₂=(V₂,A₂) c |V₁|=|V₂| и |A₁|=|A₂| будут изоморфными, если существует функция f:V₁ 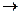V₂, такая, что {u,v} A₁ тогда и только тогда, когда f(u)f(v) A₂.

Формулировки и определения класса сложности, алгоритмов нахождения изоморфизм, инвариантов с очевидными изменениями совпадают с формулировками и определениями для графов.