Топологическое упорядочение

Направленным ациклическим графом (directed acyclic draph – DAG) является диграф без направленных циклов.

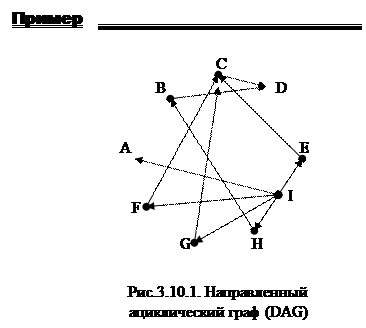Алгоритм основан на обходе в глубину (DFS) и базируется на следующем утверждении:

· диграф будет ациклическим тогда и только тогда, когда обход в глубину не содержит обратных дуг.

В общем случае под топологическим упорядочением вершин диграфа понимается такое разбиение его вершин на группы (ранги, слои), при котором:

1. вершины первой группы не имеют предшествующих вершин, а вершины последней группы – последующих;

2. вершины любой другой группы не имеют предшествующих в следующей группе;

3. вершины одной и той же группы дугами не соединены.

В результате топологического упорядочения вершин диграфа получается диграф, изоморфный данному. Этот диграф называется диграфом зависимостей.

Топологическое упорядочение вершин позволяет выявить причинно-следственные связи диграфа.

Диграф имеет топологическое упорядочение тогда и только тогда, когда он является ациклическим (DAG).

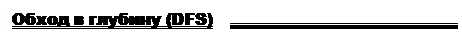Проблема топологического упорядочения вершин диграфа решается за линейное время.

Обход в глубину позволяет решать две проблемы:

· определить, имеются ли циклы в диграфе. Если циклы имеются, алгоритм останавливается после их обнаружения. В случае ацикличности диграфа DFS определяет времена завершения f[n] обхода вершин.

· Топологическое упорядочение вершин задается списком времен обнаружения, записанном в порядке уменьшения.

Сложность алгоритма – О(n+m), n=|V|, m=|E|.

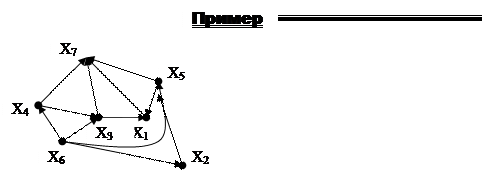
Алгоритм Фалкерсона позволяет построить топологическое упорядочение ациклического диграфа (DAG) вместе с разбиением вершин на группы (ранги, слои). Существует две разновидности алгоритма: графическая и матричная.

Графический вариант алгоритма Фалкерсона:

1. Найти вершины диграфа, в которые не входит ни одна дуга. Эти вершины образуют первую группу. Обозначим вершины первой группы v_i^I. Поместить эти вершины на вертикаль первой группы.

2. Мысленно вычеркнуть все пронумерованные вершины и дуги, из них выходящие. В получившемся диграфе найдется по крайней мере одна вершина, в которую не входит ни одна дуга. Этой вершине, входящей во вторую группу, присвоить номера v_i^II, поместить их на вертикаль второй группы и соединить дугами вершины первой и второй вертикали.

3. Повторить шаг 2 для следующих групп до тех пор, пока все вершины не будут пронумерованы, помещены на соответствующие вертикали и не соединены дугами. В результате будет построен диграф зависимостей.

Шаг 1.

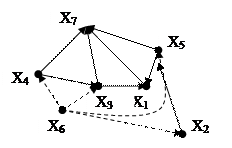
В вершину Х₆не входи ни одна дуга. Х₆ входит в первую группу вершин. Мысленно вычеркиваемые линии диграфа обозначены пунктирными линиями.

Шаг 2.

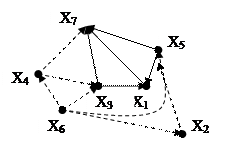
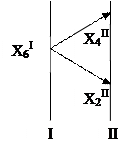В вершины не входит ни одна дуга. Вершины Х₂ и Х₄ входят во вторую группу. Обозначим эти вершины Х₂^II и Х₄^II и поместим их на вертикаль II группы. Соединяем в диграфе зависимостей вершины I и II групп соответствующими дугами. Мысленно отбрасываемые дуги помечаем в исходном диграфе пунктирными линиями.

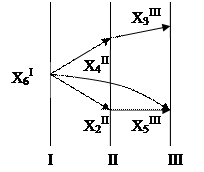
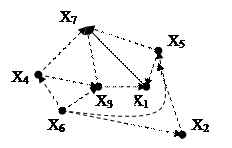
Шаг 3.

В вершины Х₃ и Х₅ не входит ни одна дуга. Вершины Х₃ и Х₅ образуют III группу. Помечаем эти вершины как Х₃^III и Х₅^III и помещаем их на третью вертикаль диграфа зависимостей. Мысленно отбрасываемые дуги в исходном диграфе помечаем штриховыми линиями.

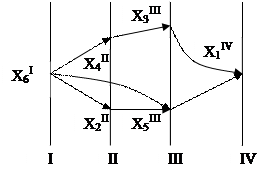
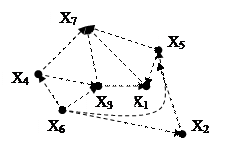
Шаг 4.

В вершину Х₁не входит ни одна дуга. Вершина Х₁входит в IV группу. Обозначим эту вершину Х₁^IV и поместим ее на четвертую вертикаль. Соединяем вершины I,II,III и IV групп соответствующими дугами. Мысленно отбрасываемую дугу помечаем штриховой линией. Непомеченной остается только вершина Х₇.

Шаг 5.

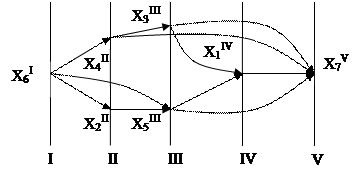Оставшаяся вершина Х₇ входит в V группу. Обозначим эту вершину Х₇^V и поместим ее на пятую вертикаль. Соединяем вершины I,II,II,IV и V групп соответствующими дугами. В результате получается полный диграф зависимостей исходного диграфа.