Интеграл наложения. Рассмотрим применение импульсной характеристики для расчета отклика цепи на сложное воздействие

Рассмотрим применение импульсной характеристики для расчета отклика цепи на сложное воздействие. Как и в предыдущем случае найдем ток в цепи при воздействии входного напряжения e(t) (рис.49).

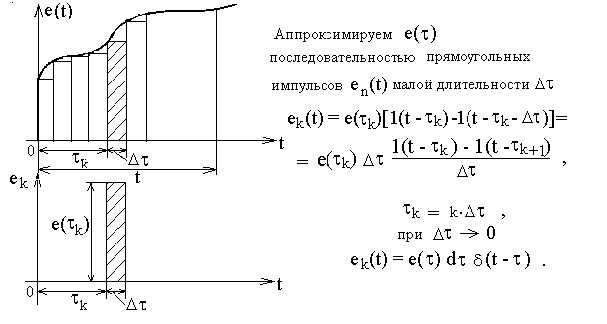
Рис. 49

Каждый отдельный прямоугольный (элементарный) импульс с площадью 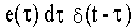вызовет ответный отклик в виде составляющей

тока

,

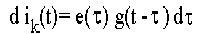
где - g(t-t) значение импульсной характеристики в момент наблюдения

t при воздействии импульса на цепь в момент t.

Результирующий отклик на всё воздействие получим, используя принцип наложения, суммируя бесконечно малые составляющие di(t), вызванные последовательностью бесконечно малых по длительности прямоугольных импульсов напряжения

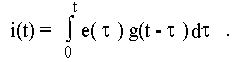
Полученный интеграл называется интегралом наложения. Используя теорему свертки, получим ещё одну форму интеграла наложения

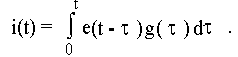
Связь между переходной и импульсной характеристиками

Поскольку h(t) и g(t) описывают одну цепь, то очевидно они жестко связаны. Выше было показано, что импульсная функция представляет собой производную от единичной функции:

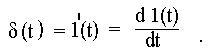
Отклик цепи на единичную функцию является переходной характеристикой h(t). А так как в линейных цепях следствия находятся в тех же соотношениях, что и вызывающие их причины, то отклик цепи на воздействие импульсной функции должен быть производной отклика единичной функции, т. е. импульсная характеристика g(t) должна быть производной от переходной характеристики h(t):

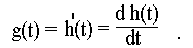
Связь между характеристиками g(t) и h(t) можно получить также, рассматривая отклик цепи на воздействие скачка напряжения Еm 1(t).

При таком воздействии отклик цепи i(t) = Em h(t).

С другой стороны

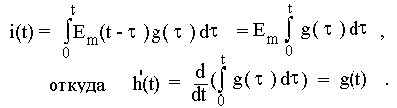
Выражение связи между импульсной и переходной характеристиками цепи несколько отличается в случае, когда переходная характеристика h(t) не равна нулю при t = 0 (рис.50).

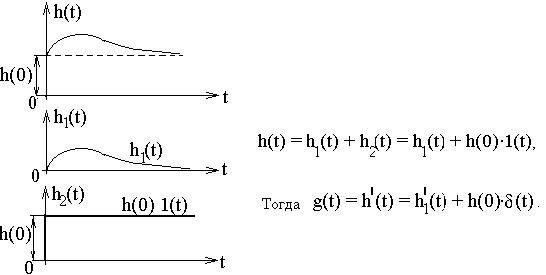
Рис. 50

Заменив переходную характеристику суммой двух функций h1(t) и h2(t) = h(0), представляющую собой скачок величиной h(0), возникающий при t = 0, получим импульсную характеристику, в которой этот скачок учтен производной второй функции h(0) d(t). Так как функции h(t) и h1(t) подобны при всех значениях t, кроме t = 0, то их производные одинаковы во всех точках, кроме скачка при t = 0.