 Из двух основных динамических характеристик, величина m
Из двух основных динамических характеристик, величина m 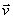 является векторной. Иногда при изучении движения точки вместо изменения самого вектора m
является векторной. Иногда при изучении движения точки вместо изменения самого вектора m 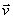 оказывается необходимым рассматривать изменение его момента. Момент вектора m
оказывается необходимым рассматривать изменение его момента. Момент вектора m 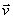 относительно данного центра О или оси z обозначается тO ( m
относительно данного центра О или оси z обозначается тO ( m 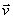 ) или mZ ( m
) или mZ ( m 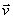 ) и называется соответственно моментом количества движения или кинетическим моментом точки относительно этого центра (оси). Вычисляется момент вектора m
) и называется соответственно моментом количества движения или кинетическим моментом точки относительно этого центра (оси). Вычисляется момент вектора m 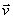 так же, как и момент силы. При этом вектор m
так же, как и момент силы. При этом вектор m 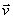 считается приложенным к движущейся точке. По модулю тO (m
считается приложенным к движущейся точке. По модулю тO (m 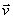 ) | = mvh, где h-
) | = mvh, где h- 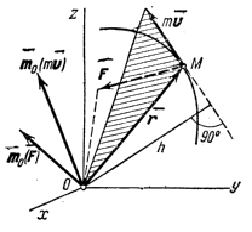 длина перпендикуляра, опущенного из центра О на направление вектора m
длина перпендикуляра, опущенного из центра О на направление вектора m 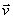 (рис.10,a).
(рис.10,a).
Теорема моментов относительно центра. Найдем для материальной точки, движущейся под действием силы F (рис.10,а), зависимость между моментами векторов т 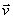 и
и 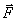 относительно какой-нибудь неподвижного центра О. В конце было показано, что m0(F)=
относительно какой-нибудь неподвижного центра О. В конце было показано, что m0(F)= 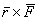 .
.
Аналогично тO(m 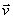 )=
)= 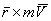 .
.
 При этом вектор m0(
При этом вектор m0( 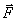 ) направлен перпендикулярно плоскости, проходящей через центр О и вектор
) направлен перпендикулярно плоскости, проходящей через центр О и вектор 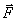 , а вектор тO(m
, а вектор тO(m 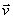 )- перпендикулярно плоскости, проходящей через центр О и вектор m
)- перпендикулярно плоскости, проходящей через центр О и вектор m 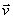 .
.
|
|
|
Рис.10
Дифференцируя выражение mO(m 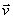 ) по времени, получаем:
) по времени, получаем:
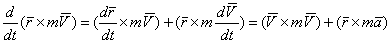 .
.
Но 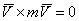 , как векторное произведение двух параллельных векторов, a
, как векторное произведение двух параллельных векторов, a 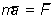 . Следовательно,
. Следовательно,
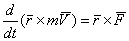
или 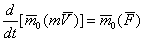 .
.
В результате мы доказали следующую теорему моментов относительно центра: производная по времени от момента количества движения точки, взятого относительно какого-нибудь неподвижного центра, равна моменту действующей на точку силы относительно того же центра. Аналогичная теорема имеетместо для моментов вектора т 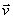 силы
силы 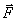 относительно какой-нибудь оси z, в чем можно убедиться, проектируя обе части равенства
относительно какой-нибудь оси z, в чем можно убедиться, проектируя обе части равенства 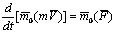 на эту ось. Математическое выражение теоремы моментов относительно оси дается формулой
на эту ось. Математическое выражение теоремы моментов относительно оси дается формулой 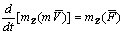 .
.
 2015-05-06
2015-05-06 687
687








