МД 2.1. Силы инерции

МД 2. Уравнения динамики атмосферы

Уравнения, определяющие детали движения воздуха, обсуждаются в данном разделе. Очевидно, естественно было бы начать с уравнения Ньютона – второго закона механики. Однако здесь следует вспомнить еще раз, что система координат, связанная с вращающейся Землей, существенно неинерциальна, и потому законы механики в такой координатной системе выглядят несколько отлично от того, к чему мы привыкли. Поскольку существует довольно много аргументов для того, чтобы использовать именно такую систему, постольку следует выяснить, к каким конкретным изменениям приводит переход к вращающейся системе координат.

МД 2.1. Силы инерции

Пусть имеется инерциальная прямоугольная система координат с осями a, b, c. Инерциальной называется система отсчета, в которой тело в отсутствие действующих на него сил движется прямолинейно и равномерно. Существует бесконечное множество инерциальных систем, движущихся относительно друг друга прямолинейно и равномерно и связанных друг с другом преобразованиями Галилея. Будем считать, что выбранная прямоугольная система является абсолютной в том смысле, что мы определяем скорости всех тел по отношению к этой системе отсчета. В этой системе вектор r материальной точки М определен своими проекциями на оси a,b,c (рис. 14.1):

, ,

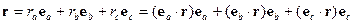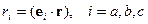где 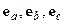- единичные орты координатных осей, операция 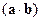означает скалярное произведение двух векторов. Пусть имеется также еще одна прямоугольная система координат с тем же началом, осями x, y, z, определенными ортами 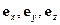, и вращающаяся с постоянной угловой скоростью Ω относительно первой[1]. Тот же вектор r во вращающейся системе координат определен проекциями на оси x, y, z:

.

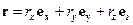Вектор абсолютной скорости точки М (скорости в исходной инерциальной системе отсчета) получается дифференцированием r по времени: 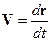. Однако в случае использования второго представления вектора следует учесть, что единичные орты вращающейся системы координат изменяют свое положение в пространстве с течением времени (изменяют свои координаты в исходной системе координат). Поэтому справедливо выражение

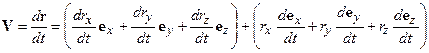. (14.1)

Выражение в первых скобках в правой части (14.1) есть ни что иное, как вектор скорости относительного движения точки (скорости точки относительно подвижной системы координат, то есть, скорости изменения проекций радиус-вектора точки на оси подвижной системы). Выражение во вторых скобках - вклад в абсолютную скорость за счет движения вращающейся системы относительно неподвижной (скорость переносного движения).

Орты вращающейся системы координат являются обычными векторами, и для их скорости в неподвижной системе координат имеем

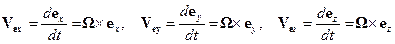, (14.2)

где 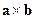означает векторное произведение двух векторов: длина результирующего вектора численно равна площади параллелограмма, построенного на исходных векторах (произведение длин векторов на синус угла между ними), а направление определяется по правилу винта при вращении первого вектора в направлении второго. В частности, длина произведения 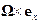есть расстояние конца орта 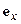до оси вращения, умноженное на угловую скорость вращения, и равна линейной скорости вращения конца орта. Для вычисления векторного произведения часто используют следующее равенство

.

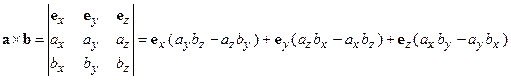Здесь прямые вертикальные линии обозначают детерминант (определитель).

Подставляя соотношения (14.2) в формулу для абсолютной скорости (14.1), находим

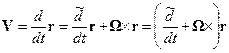, (14.3)

где оператор 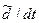означает дифференцирование по времени в предположении, что вращающаяся система координат покоится, то есть, орты осей координат не зависят от времени. Иными словами, операция 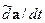определяет относительную скорость изменения вектора 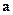. Выражение (14.3) справедливо для любого вектора, приложенного к началу вращающейся системы координат. Поэтому для ускорения материальной точки получаем

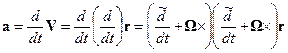. (14.4)

Если раскрыть произведение в правой части (14.4), получим с учетом постоянства угловой скорости

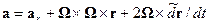. (14.5)

Здесь 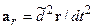называют ускорением относительного движения, второй член в правой части - центростремительным ускорением, а третий - ускорением Кориолиса.

Приведенные формулы становятся актуальными, при переходе к системе координат, связанной с Землей. Очевидно, такая система координат не является инерциальной, в первую очередь, из-за вращения Земли вокруг своей оси. В то же время второй закон Ньютона, определяющий ускорение движения в зависимости от действующих сил, справедлив только в инерциальных системах отсчета.

Очень хорошей инерциальной системой является так называемая гелиоцентрическая система координат, связанная с Солнцем, и с осями координат, зафиксированными по отношению к другим звездам. В этой системе Земля совершает движение по эллиптической траектории вокруг Солнца и вращается вокруг своей оси.

С достаточной степенью точности для изучения атмосферных движений оказывается инерциальной система координат, движущаяся вокруг Солнца вместе с Землей, но не вращающаяся вместе с Землей вокруг ее оси. Однако и она не слишком удобна для использования, поскольку мы привыкли рассматривать атмосферные движения по отношению к покоящейся Земле, то есть, рассматривать относительные движения, относительные скорости и относительные ускорения в системе координат, вращающейся вместе с Землей. В качестве такой системы обычно выбирают так называемую горизонтальную систему координат [2]. Тогда в правую часть уравнения для относительного ускорения следует ввести поправочные члены, обусловленные неинерциальностью системы отсчета.

Эти поправочные члены называют силами инерции, а именно, центробежной силой и силой Кориолиса. Будучи отнесенными к единице массы, они численно равны соответственно второму и третьему слагаемым в (14.5), взятым с обратным знаком. С учетом введенных сил инерции относительное ускорение материальной точки получается отличным от нуля, несмотря на отсутствие реальных действующих сил, а относительная траектория получается криволинейной (хотя она прямолинейна в инерциальной гелиоцентрической системе отсчета). Классическим примером, демонстрирующим эффекты неинерциальности системы отсчета, скрепленной с Землей, является маятник Фуко[3].

В дальнейшем уравнения движения будут рассматриваться, как правило, в системе координат, вращающейся вместе с Землей. При этом для производной по времени мы будем использовать обычное обозначение - 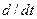, не забывая, однако, что речь идет об относительном движении, и о необходимости учета сил инерции.

Центробежная сила там, где она имеет наибольшие значения (вблизи экватора, где велико расстояние до оси вращения), близка по направлению к силе тяжести, составляет малую долю по сравнению с ней и может быть учтена посредством незначительной коррекции вектора силы тяжести. Поэтому в дальнейшем практически всюду мы не будем специально выделять эту силу.

Сила Кориолиса зависит от величины и направления скорости относительного движения и может существенно влиять на последнее. Поэтому она, как правило, всегда будет явно присутствовать в уравнениях относительного движения.

Приведенные соотношения вполне достаточны для рассмотрения атмосферных движений. Тем не менее, их легко обобщить на более сложные случаи, когда начало вращающейся системы отсчета перемещается в пространстве, и вектор угловой скорости вращения меняет величину и направление.