Рассмотрим на примере трех сил. Пусть к телу в точках А, В, С приложена плоская система сил { 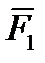 ,
, 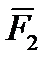 ,
, 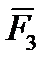 } (рис. 3.9). Выберем произвольную точку О, перенесем в нее силы
} (рис. 3.9). Выберем произвольную точку О, перенесем в нее силы 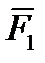 ,
, 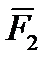 ,
, 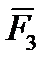 . Согласно лемме Пуансо получим сходящуюся систему сил {
. Согласно лемме Пуансо получим сходящуюся систему сил { 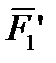 ,
, 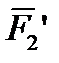 ,
, 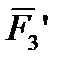 } и систему пар (
} и систему пар (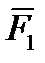 ,
, 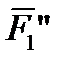 ), (
), (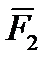 ,
, 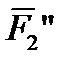 ), (
), (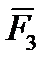 ,
, 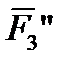 ) с моментами М1, М2, М3, равными моментам сил
) с моментами М1, М2, М3, равными моментам сил 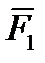 ,
, 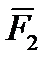 ,
, 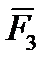 относительно точки О.
относительно точки О.
Сложив 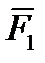 ,
, 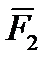 ,
, 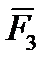 по правилу многоугольника, получим:
по правилу многоугольника, получим:
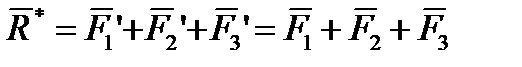 . (3.7)
. (3.7)
Вектор 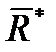 , равный геометрической сумме сил системы называется главным вектором данной системы сил.
, равный геометрической сумме сил системы называется главным вектором данной системы сил.
Теперь сложим пары сил, в результате получим пару сил, с моментом
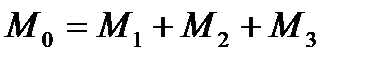 . (3.8)
. (3.8)
М0 – равен алгебраической сумме моментов сил и называется главным моментом системы сил относительно точки.
Рис. 3.9
Теорема Вариньона. Если система сил приводится к равнодействующей, то момент равнодействующей относительно любой точки равен сумме моментов всех сил системы относительно той же точки.
Доказательство:
Пусть система сил { 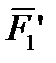 ,
, 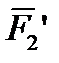 ,
, 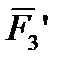 } имеет равнодействующую
} имеет равнодействующую 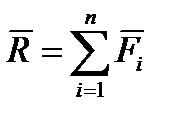 (рис. 3.10), приложенную в некоторой точке О1 плоскости действия сил. Перенесем вектор
(рис. 3.10), приложенную в некоторой точке О1 плоскости действия сил. Перенесем вектор 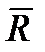 в точку О, при этом согласно лемме Пуансо необходимо добавить пару (
в точку О, при этом согласно лемме Пуансо необходимо добавить пару (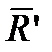 ,
, 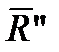 ) с моментом М0=М(R). Но М0 – главный момент системы сил относительно точки О, который равен алгебраической сумме моментов всех сил системы относительно этой точки:
) с моментом М0=М(R). Но М0 – главный момент системы сил относительно точки О, который равен алгебраической сумме моментов всех сил системы относительно этой точки: 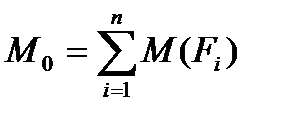 . Следовательно
. Следовательно 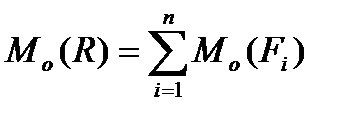 .
.
Рис. 3.10
Следствия из теоремы:
1. Главный вектор 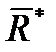 не изменится при изменении центра приведения.
не изменится при изменении центра приведения.
2. Главный момент при перемене центра приведения изменится на величину момента силы 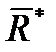 , приложенной в точке О, относительно нового центра.
, приложенной в точке О, относительно нового центра.
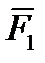 ,
, 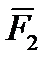 ,
, 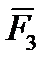 } (рис. 3.9). Выберем произвольную точку О, перенесем в нее силы
} (рис. 3.9). Выберем произвольную точку О, перенесем в нее силы 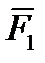 ,
, 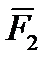 ,
, 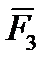 . Согласно лемме Пуансо получим сходящуюся систему сил {
. Согласно лемме Пуансо получим сходящуюся систему сил { 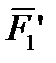 ,
, 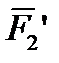 ,
, 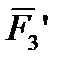 } и систему пар (
} и систему пар (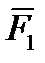 ,
, 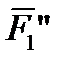 ), (
), (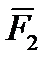 ,
, 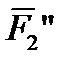 ), (
), (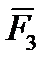 ,
, 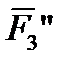 ) с моментами М1, М2, М3, равными моментам сил
) с моментами М1, М2, М3, равными моментам сил 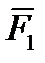 ,
, 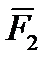 ,
, 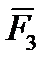 относительно точки О.
относительно точки О.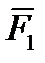 ,
, 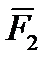 ,
, 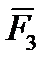 по правилу многоугольника, получим:
по правилу многоугольника, получим: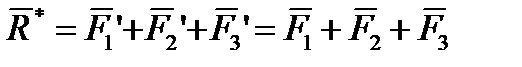 . (3.7)
. (3.7)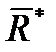 , равный геометрической сумме сил системы называется главным вектором данной системы сил.
, равный геометрической сумме сил системы называется главным вектором данной системы сил.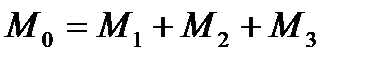 . (3.8)
. (3.8)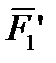 ,
, 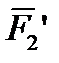 ,
, 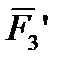 } имеет равнодействующую
} имеет равнодействующую 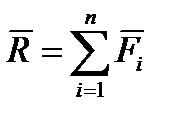 (рис. 3.10), приложенную в некоторой точке О1 плоскости действия сил. Перенесем вектор
(рис. 3.10), приложенную в некоторой точке О1 плоскости действия сил. Перенесем вектор 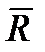 в точку О, при этом согласно лемме Пуансо необходимо добавить пару (
в точку О, при этом согласно лемме Пуансо необходимо добавить пару (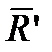 ,
, 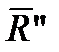 ) с моментом М0=М(R). Но М0 – главный момент системы сил относительно точки О, который равен алгебраической сумме моментов всех сил системы относительно этой точки:
) с моментом М0=М(R). Но М0 – главный момент системы сил относительно точки О, который равен алгебраической сумме моментов всех сил системы относительно этой точки: 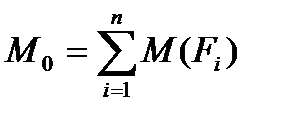 . Следовательно
. Следовательно 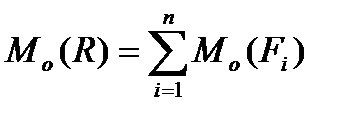 .
.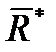 не изменится при изменении центра приведения.
не изменится при изменении центра приведения.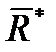 , приложенной в точке О, относительно нового центра.
, приложенной в точке О, относительно нового центра. 2015-04-20
2015-04-20 539
539








