2015-04-20
573
Евклидовым пространством называется линейное векторное пространство с заданным на нем скалярным произведением.
Скалярным произведением на векторном пр-ве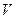 
наз. отображение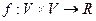 
1) симметричность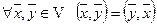 
;
2) линейность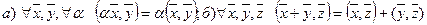 
;
3) 
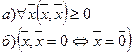
Пусть Е-п-мерное Евклидовое пр-во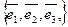 
- базис тогда 
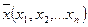можно расписать в виде 
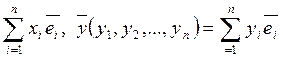тогда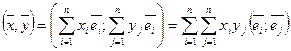 
обозначим 
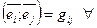тогда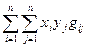 
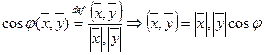
2 вектора ортогональны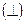 
равносильно тому, что угол между ними =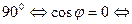 
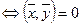, т. е. 2 вектора ортогональны т. и т. т. к. их скалярное произведение =0.
Система векторов называется ортогональной, если вектора этой системы попарно ортогональны.
Система векторов наз. ортонормированной, если она является ортогональной и все вектора этой системы имеют единичную длину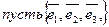 
ортонормированный базис, тогда
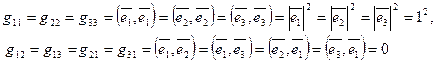
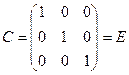
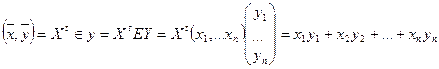
в ортонормированном базисе скалярное произведение = сумме произведений соответствующих координат.
Пусть в евклидовом пр-ве Е задан ортонормированный базис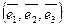 
. Тогда вектор 
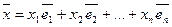. Домножим скалярно правую и левую части последнего равенства на 
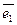. Получим:
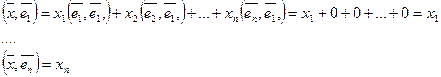
Т. о., в ортонормированном базисе координаты вектора равны скалярному произведению этого вектора на соответствующий базисный вектор.
Из любой системы векторов евклидового пространства можно получить ортонормированный базис. Значит в любом евклидовом пространстве 
ортонормированный базис.
