2015-04-20
1099
Если вероятность наступления события A в каждом из независимых испытаний постоянна и 0 < p < 1, то вероятность того, что в n испытаниях событие произойдет от k 1 до k 2 (при достаточно большом n) равна
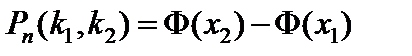, (37)
где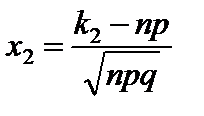 
;
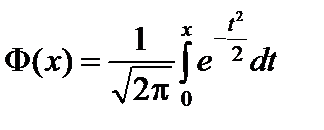– функция Лапласа.
Функция Лапласа Φ(х) существует при любом действительном значении x. Свойства функции:
1) функция Лапласа – нечетная функция, т. е. Φ(– х) = – Φ(х);
2) при возрастании х от 0 до 5 Φ(х) возрастает от 0 до 0,5. Для
x > 5 Φ(х)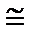 
0,5.
Таблица значений Φ(х) для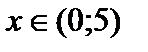 
находится в прил. 2.
Пример 1.31. На оптовую базу поступает в среднем 70 % продукции высшего сорта. Какова вероятность того, что в партии из 1000 изделий проверенных товароведом, число изделий высшего сорта, заключено между 652 и 760?
Решение. Событие A – «появление изделия высшего сорта», вероятность наступления события в отдельном испытании равна p = 0,7. Требуется найти: P 1000(652;760) = Φ(х 2) – Φ(х 1).
Расчет производим по следующей схеме:
; 
;
;
; 
.
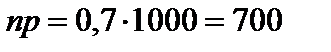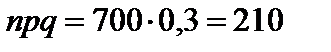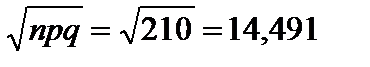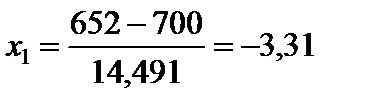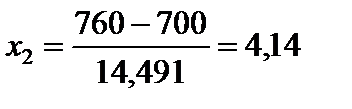По таблице прил. 2 определяем:
Ф(х 1) = Ф(–3,31) = –0,4991; Ф(х 2) = Ф(4,14) = 0,4999.
|
|
|
Искомая вероятность Р 1000(652; 760) = 0,4999 + 0,4991 = 0,999.
Пример 1.32. Посажено 400 деревьев. Какова вероятность того, что число прижившихся деревьев больше 250, если вероятность того, что отдельное дерево приживется, равна 0,8?
Решение. Число прижившихся деревьев должно удовлетворять неравенству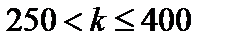 
, поэтому вероятность этого события равна:
Р 400(250; 400) = Ф(х 1) – Ф(х 2) = 0,999.
