Для таблицы с постоянным шагом значения аргумента образуют арифметическую прогрессию 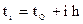 , где h – шаг таблицы. Запишем таблицу в виде двух столбцов
, где h – шаг таблицы. Запишем таблицу в виде двух столбцов 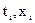 . Из каждого значения функции
. Из каждого значения функции 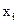 вычтем предыдущее и разность запишем в следующем столбце между теми значениями, из которых получена разность (то есть,
вычтем предыдущее и разность запишем в следующем столбце между теми значениями, из которых получена разность (то есть, 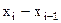 ):
):
Таблица 3
Таблица обыкновенных и центральных разностей
| T | X | разности 1 порядка | разности 2 порядка | разности 3 порядка | разности 4 порядка | разности 5 порядка | разности 6 порядка |
| t-3 | x-3 | ||||||
| D1-5/2 | |||||||
| t-2 | x-2 | D2-2 | |||||
| D1-3/2 | D3-3/2 | ||||||
| t-1 | x-1 | D21 | D4-1 | ||||
| D1-1/2 | D3-1/2 | D5-1/2 | |||||
| t0 | x0 | D10 | D20 | D30 | D40 | D50 | D60 |
| D11/2 | D31/2 | D51/2 | |||||
| t1 | x1 | D21 | D41 | ||||
| D13/2 | D33/2 | ||||||
| t2 | x2 | D22 | |||||
| D15/2 | |||||||
| t3 | x3 |
Отметим, что в принятых обозначениях – верхний индекс – порядок разности; нижний индекс – среднее арифметическое индексов функции, из которых разность получена.
|
|
|
В таблице введены центральные разности
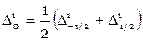 ,
, 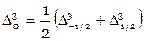 ,
, 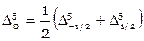 .
.
По величине разностей можно судить о том, какой степени интерполяционный полином необходим для достижения точности значений, соответствующей точности узлов таблицы. Если табличная функция допускает приближение полиномом n-й степени, то в этой таблице разности n-го порядка будут почти постоянными. Разности следующего порядка будут пренебрежимо малы.
Отметим, что свойство постоянства n-х разностей справедливо только для таблиц точных значений полиномов. Если значения в узлах таблицы известны с некоторой точностью и погрешность округления равна половине единицы последнего разряда табличного значения функции, то вспомним, что при вычитании двух приближенных чисел абсолютные погрешности складываются. Отсюда погрешность 1-й разности равна единице последнего разряда; погрешность 2-й разности равна 2-м единицам последнего разряда; погрешность 3-й разности равна 4-м единицам последнего разряда и так далее.
| Разности | x | Dx | D2x | D3x | D4x | D5x | … | Dkx |
| Абсолютная погрешность | 1/2 | … | 2k-1 |
Таким образом, из-за неизбежной погрешности округления на практике обычно не следует пользоваться разностями выше 4-5-го порядков.
Будем считать, что разности k-го порядка практически равны нулю, если их сумма и величина каждой из них меньше, чем соответствующая погрешность округления, а знаки стоят в беспорядке или чередуются.
Построение таблицы разностей есть единственный способ выяснить нужную степень интерполяционного полинома, то есть число узлов, необходимое для удовлетворительного приближения.
|
|
|
Проконтролировать вычисление таблицы разностей можно просуммировав сами разности:
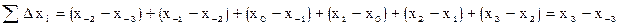 Соответственно
Соответственно
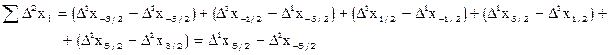 и так далее.
и так далее.
Обобщая, имеем: сумма значений в каждом столбце разностей равна разности между последним и первым значениями предыдущего столбца.
Пример построения таблицы обыкновенных и центральных разностей
| T | X | разности 1 порядка | разности 2 порядка | разности 3 порядка |
| t-3=-0.3 | x-3=-0.027 | |||
| D1-5/2=0.019 | ||||
| t-2=-0.2 | x-2=-0.008 | D2-2=-0.012 | ||
| D1-3/2=0.007 | D3-3/2=0.006 | |||
| t-1=-0.1 | x-1=-0.001 | D2-1=-0.006 | ||
| D1-1/2=0.001 | D3-1/2=0.006 | |||
| t0=0 | x0=0 | D10=0.001 | D20=0 | D30=0.006 |
| D11/2=0.001 | D31/2=0.006 | |||
| t1=0.1 | x1=0.001 | D21=0.006 | ||
| D13/2=0.007 | D33/2=0.006 | |||
| t2=0.2 | x2=0.008 | D22=0.012 | ||
| D15/2=0.019 | ||||
| t3=0.3 | x3=0.027 |
Пример. Построим таблицу обыкновенных разностей для функции 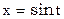 с шагом 1О на отрезке
с шагом 1О на отрезке 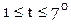 с точностью до тысячных, определим, какие из них практически равны нулю. Вычисленные разности проконтролируем.
с точностью до тысячных, определим, какие из них практически равны нулю. Вычисленные разности проконтролируем.
| t | x = sin t | разности 1 порядка | разности 2 порядка |
| 0.017 | |||
| 0.018 | |||
| 0.035 | -0.001 | ||
| 0.017 | |||
| 0.052 | 0.001 | ||
| 0.018 | |||
| 0.070 | -0.001 | ||
| 0.017 | |||
| 0.087 | 0.001 | ||
| 0.018 | |||
| 0.105 | -0.001 | ||
| 0.017 | |||
| 0.122 | |||
| суммы | 0.105 | -0.001 | |
| Контрольные разности | 0.122-0.017=0.105 | 0.017-0.018=-0.001 | -0.001-(-0.001)=0 |
 2015-05-14
2015-05-14 1016
1016








