Важной задачей регрессионного анализа состоит в построении прогнозов зависимой переменной в зависимости для выбранных значений объясняющей переменной. Значение зависимой переменной при значении х объясняющей переменной должно удовлетворять уравнению 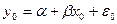 , где ɛ0 реализация случайного члена.
, где ɛ0 реализация случайного члена.
Допустим модели парной линейной регрессии построено ур-ие y=a+bx. Коэффициенты а, б, предполагаются значимыми. Возможен прогноз двух типов. Мат ожидание значения зависимой переменной при x=x0 равно Е(y|x0)= α+ βx0. согласно теореме гаусса-Маркова прогнозом этой величины служит 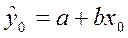 .
.
Возможны два подхода: первый-насколько прогнозное значение может отклонится от условного мат ожидания Е(у|х0). Второй –насколько прогнозное значение у0 зависимой переменной может отклониться от ее прогнозного значения.
1. Доверительный интервал для ожидаемого значения зависимой переменной. Основой для построения доверительного интервала является отношение
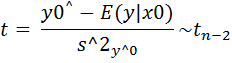
Где оценка 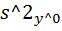 дисперсия прогнозного значения y^0 зависимой переменной определяется выражением
дисперсия прогнозного значения y^0 зависимой переменной определяется выражением
|
|
|
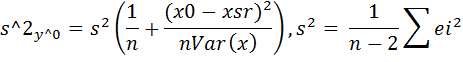
Для выбранного уровня значимости 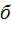 определяется критическое значение
определяется критическое значение 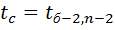 статистики Стьюдента с n-2 степенями свободы.
статистики Стьюдента с n-2 степенями свободы.
Ответ на вопрос о точности прогноза дается в форме доверительного интервала ожидаемого значения зависимой переменной, построенного с уровнем надежности 1- 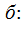
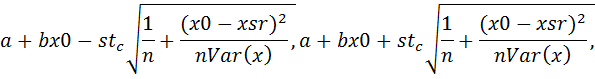
Где s стандартная ошибка случ члена модели.
2) Доверительный интервал для индивидуального значения зависимой переменной. В этом случае распределение Стьюдента имеет величина
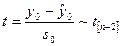 .
.
Построение доверительного интервала сводится к вычислению 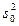 -оценки дисперсии var(e0)=
-оценки дисперсии var(e0)= 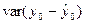 отклонение значения
отклонение значения 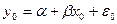 зависимой переменной от ее прогнозного значения. Она равна
зависимой переменной от ее прогнозного значения. Она равна
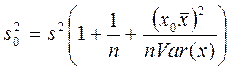
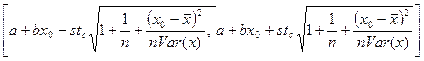
Здесь также 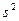 - оценка дисперсии случайного члена, а tc- критическое значение распределения Стьюдента с n-2 степенями свободы.
- оценка дисперсии случайного члена, а tc- критическое значение распределения Стьюдента с n-2 степенями свободы.
11. Множественная линейная регрессия. Матричная форма записи.
Модель множественной линейной регрессии является обобщением модели парной линейной регрессии и записывается в следующем виде: y= β1x1+ β2x2+…+βkXk+Ɛ, где у- зависимая переменная, β1,β2…βk- коэффициенты регрессии, Ɛ-случайный член, включение которого в уравнение регрессии обусловлено теми же причинами, что и в случае парной регрессии. На первый взгляд может показаться, что модель y= β1x1+ β2x2+…+βkXk+Ɛ не может содержать постоянный член, такой, как £ в уравнении y=£ + βх+Ɛ модели парной линейной регрессии. При к=2 и х1=1 уравнение y= β1x1+ β2x2+…+βkXk+Ɛ переходит в уравнение парной линейной регрессии.
Пусть имеется выборка, состоящая из n наблюдений зависимой и объясняющих переменных Yi,Xi1,Xi2,…,Xik, i=1,2..,n, для которых уравнение регрессии y= β1x1+ β2x2+…+βkXk+Ɛ запишется в виде системы уравнений Yi= β1Xi1+β2Xi2+…+βkXik+ Ɛi i=1,2,…,n. Определим векторы-столбцы и матрицу: y= 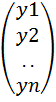 X=
X= 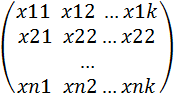 β=
β=  Ɛ=
Ɛ= 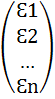
Столбец у и матрица Х содержат данные выборки. В столбце 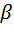 записаны неизвестные коэффициенты, которые следует оценить по имеющейся выборке, Ɛ- столбец случайных членов, которые ненаблюдаемы. В случае, когда модель содержит постоянный член, первый столбец матрицы Х состоит из единиц. Используя эти обозначения можно записать в компактной матричной форме: у=Хβ+ Ɛ.
записаны неизвестные коэффициенты, которые следует оценить по имеющейся выборке, Ɛ- столбец случайных членов, которые ненаблюдаемы. В случае, когда модель содержит постоянный член, первый столбец матрицы Х состоит из единиц. Используя эти обозначения можно записать в компактной матричной форме: у=Хβ+ Ɛ.
|
|
|
12.Случайные векторы и ковариационная матрица.
Для произвольного случайного вектора z=(Z1,Z2,…,Zn)’ определим матричное ожидание E(z)=(E(Z1),E(Z2),…,E(Zn))’ и ковариационную матрицу V(z)=E 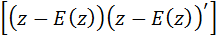 . Как и для вектора, математическое ожидание матрицы- это матрица, элементами которой являются математические ожидания исходной матрицы. Поэтому ковариационная матрица
. Как и для вектора, математическое ожидание матрицы- это матрица, элементами которой являются математические ожидания исходной матрицы. Поэтому ковариационная матрица
V(z)= 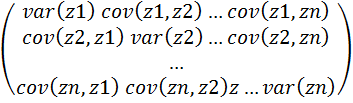
По диагонали ковариационной матрицы V(z) в (i,i)-й позиции записана дисперсия (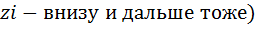
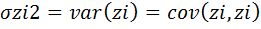 , а в(i,j)-й позиции записана ковариация
, а в(i,j)-й позиции записана ковариация 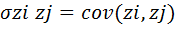 .
.
Отметим следующее свойство ковариационной матрицы. Если с- постоянный вектор размерности n, А- детерминированнная квадратная матрица порядка n, то V(z+c)= V(z), V(Az)=AV(z)A’. Для случайного вектора z запись z~(µ,V) будет означать, что математическое ожидание z равно вектору µ, a V –его ковариационная матрица.
Через In обозначим единичную матрицу порядка n, т.е. квадратную матрицу, которой элементы главной диагонали равны 1, а остальные элементы 0.
13.Классическая модель множественной линейной регрессии. Предположения и их интерпретация.
Классическая модель множественной линейной регрессии имеет вид у=Хβ+ Ɛ.Предположения классической модели множественной линейной регрессии.
1) Объясняющие переменные х1,х2,…,хк неслучайные, а ранг матрицы Х равен к, к≤n, т.е. матрица Х имеет полный ранг. Это значит, что элементы матрицы Х детерминированные величины, а ее столбцы линейно независимы.
2)Вектор случайных членов Ɛ~(0, σ2 In). Следовательно, предполагается, что каждая компонента имеет нулевое математическое ожидание, дисперсию, равную,а ковариация разных равна нулю.
2‘ Если дополнительно предполагается, что компоненты вектора Ɛ имеют нормальное распределение.то условие 2 заменяется на Ɛ~N(0, σ2 In).
 2015-05-18
2015-05-18 4989
4989
