2015-05-18
1204
Парная (простая) линейная регрессия представляет собой модель, где среднее значение зависимой (объясняемой) переменной рассматривается как функция одной независимой (объясняющей) переменной x, т.е. это модель вида:
(2.1)
Так же y называют результативным признаком, а x признаком-актором. Знак «^» означает, что между переменными x и y нет строгой функциональной зависимости. Практически в каждом отдельном случае величина y складывается из двух слагаемых:
(2.2)
где y – фактическое значение результативного признака; 
- теоретическое значение результативного признака, найденное исходя из уравнения регрессии; 
– случайная величина, характеризующая отклонения реального значения результативного признака от теоретического, найденного по уравнению регрессии. Случайная величина называется также возмущением. Она включает влияние не учтенных в модели факторов, случайных ошибок и особенностей измерения. Ее присутствие в модели порождено тремя источниками: спецификацией модели, выборочным характером исходных данных, особенностями измерения переменных.
|
|
|
Различают линейные и нелинейные регрессии.
Линейная регрессия: 
.
Нелинейные регрессии делятся на два класса: регрессии, нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам, и регрессии, нелинейные по оцениваемым параметрам. Например:
регрессии, нелинейные по объясняющим переменным:
- полиномы разных степеней 
;
- равносторонняя гипербола 
;
регрессии, нелинейные по оцениваемым параметрам:
- степенная 
;
- показательная 
;
- экспоненциальная 
.
Построение уравнения регрессии сводится к оценке ее параметров. Для оценки параметров регрессий, линейных по параметрам, используют метод наименьших квадратов (МНК). МНК позволяет получить такие оценки параметров, при которых сумма квадратов отклонений фактических значений результативного признака y от теоретических 
минимальна, т.е.
(2.3)
Для линейных и нелинейных уравнений, приводимых к линейным, решается следующая система относительно a и b:
(2.4)
Можно воспользоваться готовыми формулами, которые вытекают непосредственно из решения этой системы:
(2.5)
где 
- ковариация признаков x и y, 
-дисперсия признака x и
.
(Ковариация – числовая характеристика совместного распределения двух случайных величин, равная математическому ожиданию произведения отклонений этих случайных величин от их математических ожиданий. Дисперсия – характеристика случайной величины, определяемая как математическое ожидание квадрата отклонения случайной величины от ее математического ожидания. Математическое ожидание – сумма произведений значений случайной величины на соответствующие вероятности.)
|
|
|
Тесноту связи изучаемых явлений оценивает линейный коэффициент парной корреляции 
для линейной регрессии 
:
(2.6)
и индекс корреляции 
- для нелинейной регрессии 
где 
– общая дисперсия результативного признака y; 
– остаточная дисперсия, определяемая исходя из уравнения регрессии
Оценку качества построенной модели даст коэффициент (индекс) детерминации 
(для линейной регрессии) либо 
(для нелинейной регрессии), а также средняя ошибка аппроксимации.
Средняя ошибка аппроксимации – среднее отклонение расчетных значений от фактических:
(2.7)
Допустимый придел значений 
- не более 10%.
Средний коэффициент эластичности 
показывает, на сколько процентов в среднем по совокупности изменится результат у от своей средней величины при изменении фактора x на 1% от своего среднего значения:
(2.8)
После того как найдено уравнение линейной регрессии, проводится оценка значимости как уравнения в целом, так и отдельных его параметров. Проверить значимость уравнения регрессии – значит установить, соответствует ли математическая модель, выражающая зависимость между переменными, экспериментальным данным и достаточно ли включенных в уравнение объясняющих переменных (одной или нескольких) для описания зависимой переменной.
Оценка значимости уравнения регрессии в целом производится на основе F -критерия Фишера, которому предшествует дисперсионный анализ. Согласно основной идее дисперсионного анализа, общая сумма квадратов отклонений переменной y от среднего значения y раскладывается на две части – «объясненную» и «необъясненную»:
где 
– общая сумма квадратов отклонений; 
– сумма квадратов отклонений, объясненная регрессией (или факторная сумма квадратов отклонений); 
– остаточная сумма квадратов отклонений, характеризующая влияние неучтенных в модели факторов.
Схема дисперсионного анализа имеет вид, представленный в таблице 1.1 (n – число наблюдений, m – число параметров при переменной x).
Таблица 2.1
| Компоненты дисперсии | Сумма квадратов | Число степеней свободы | Дисперсия на одну степень свободы |
| Общая |
| n-1 | 
|
| Факторная |
| m | 
|
| Остаточная |
| n-m-1 | 
|
Определение дисперсии на одну степень свободы приводит дисперсии к сравнимому виду (напомним, что степени свободы – это числа, показывающие количество элементов варьирования, которые могут принимать произвольные значения, не изменяющие заданных характеристик). Сопоставляя факторную и остаточную дисперсии в расчете на одну степень свободы, получим величину F -критерия Фишера:
.
Фактическое значение F -критерия Фишера сравнивается с табличным значением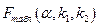 
при уровне значимости 
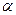и степенях свободы 
и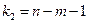 
. При этом, если фактическое значение F - критерия больше табличного, то признается статистическая значимость уравнения в целом.
Для парной линейной регрессии m =1, поэтому
Величина F -критерия связана с коэффициентом детерминации , и ее можно рассчитать по следующей формуле:
(2.9)
Для оценки статистической значимости параметров регрессии и корреляции рассчитываются t -критерий Стьюдента и доверительные интервалы каждого из показателей. Оценка значимости коэффициентов регрессии и корреляции с помощью t -критерия Стьюдента проводится путем сопоставления их значений с величиной случайной ошибки:
(2.10)
Стандартные ошибки параметров линейной регрессии и коэффициента корреляции определяются по формулам:
(2.11)
Сравнивая фактическое и критическое (табличное) значения t - статистики – tтабл и tфакт – делаем вывод о значимости параметров регрессии и корреляции. Если tтабл < tфакт то параметры a, b и rxy не случайно отличаются от нуля и сформировались под влиянием систематически действующего фактора x. Если tтабл > tфакт, то признается случайная природа формирования a, b или rxy.
|
|
|
Для расчета доверительного интервала определяем предельную ошибку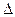 
для каждого показателя:
Формулы для расчета доверительных интервалов имеют следующий вид:
Если в границы доверительного интервала попадает ноль, т.е. нижняя граница отрицательна, а верхняя положительна, то оцениваемый параметр принимается нулевым, так как он не может одновременно принимать и положительное, и отрицательное значения.
Связь между F -критерием Фишера и t -статистикой Стьюдента выражается равенством
(2.12)
В прогнозных расчетах по уравнению регрессии определяется предсказываемое индивидуальное значение y0 как точечный прогноз при x = x0, т.е. путем подстановки в линейное уравнение 
соответствующего значения x. Однако точечный прогноз явно нереален, поэтому он дополняется расчетом стандартной ошибки
(2.13)
где 
, и построением доверительного интервал прогнозного значения 
:
