Пример. Рассмотрим процесс функционирования системы ­– автомобиль, находящийся на гарантийном сервисном обслуживании

Рассмотрим процесс функционирования системы ­– автомобиль, находящийся на гарантийном сервисном обслуживании. Пусть автомобиль (система) в течение одной смены (месяца) может находиться в одном из двух состояний: исправном S₁ и неисправном S₂. Граф состояний системы представлен на рисунке (рис. 2.2).

S1

S2

Рис. 2.2. Граф возможных состояний системы S

Пусть матрица переходных вероятностей имеет вид: 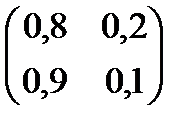, где

p₁₁ = 0,8 – вероятность того, что автомобиль останется в исправном состоянии;

p₁₂ = 0,2 – вероятность перехода автомобиля из состояния «исправен» в состояние «неисправен»;

p₂₁ = 0,9 – вероятность перехода автомобиля из состояния «неиспра­вен» в состояние «исправен»;

p ₂₂ = 0,1 – вероятность того, что автомобиль останется в состоянии «неисправен».

Пусть в начальный момент времени автомобиль был исправен, т. е. P₁ (0) = 1, P₂(0) = 0. Тогда, найдём вероятности состояний системы в момент времени t = 1:

P₁ (1) = P₁ (0) p₁₁ + P₂ (0) p₂₁ = 0,8

P₂ (1) = P₁(0) p₁₂ + P₂ (0) p₂₂ = 0,2.

В момент времени t = 2:

P₁ (2) = P₁ (1) p₁₁ + P₂ (1) p₂₁ = 0,8×0,8 + 0,2×0,9 = 0,82

P₂ (2) = P₁(1) p₁₂+ P₂ (1) p₂₂ = 0,8×0,2 + 0,2×0,1 = 0,18.

В момент времени t = 3:

P₁ (3) = P₁(2) p₁₁ + P₂(2)p₂₁ = 0,82×0,8 +0,18×0,9 = 0,818

P₂ (3) = P₁(2) p₁₁ +P₂(2)p₂₁ =0,182.

Т. е. после трёх суток автомобиль будет находиться в состоянии «исправен» с вероятностью 0,818, а «неисправен» – с вероятностью 0,182.

Заметим, что формулу (2.1) можно переписать в матричном виде:

P (k) = P (k-1) × P, (2.2)

где P (k) = (P₁(k), P₂ (k), …,P_n (k)) – вектор вероятностей состояний системы в момент k;

P = {p_ij} – матрица переходных вероятностей.

Действительно:

(1,0) × 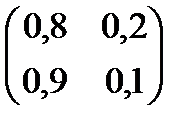= (0,8;0,2)

(0,8;0,2) × 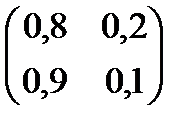= (0,82;0,18)

(0,82;0,18) × 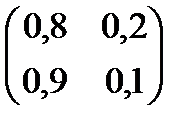= (0,818;0,182).

В матричном виде вычисления вести удобней.

2.3. Непрерывные цепи Маркова

Марковский случайный процесс с дискретными состояниями и непрерывным временем называется непрерывной цепью Маркова при условии, что переход системы из состояния в состояние про­исходит не в фиксированные, а в случайные моменты времени.

В экономике часто встречаются ситуации, которые указать за­ранее невозможно. Например, любая деталь или агрегат автомоби­лямогут выйти из строя в любой, непредсказуемый заранее мо­мент времени. Для описания таких систем в отдельных случаях можно использовать математический аппарат непрерывной цепи Маркова.

Пусть система характеризуется п состояниями S₀, S_1, S_2,..., S_n, а переход из состояния в состояние может осуществляться в любой момент времени. Обозначим по-прежнему через P_i (t) вероятность того, что в момент времени t система S будет находиться в состоянии S_i. Требуется определить для любого t вероятности P₀ (t), P₁ (t),... P_n (t).

Для процесса с непрерывным временем вместо переходных ве­роятностей p _ij рассматриваются плотности вероятностей перехода 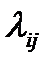,представляющие собой предел отношения вероятности перехо­да системы за время 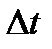из состояния S_i в S_j:.

.

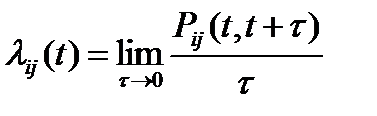Если 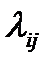= const, то процесс называется однородным, если плот­ность вероятности зависит от времени 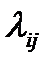= 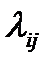(t), то процесс – не­однородный.

При рассмотрении непрерывных марковских процессов приня­то представлять переходы системы S из состояния в состояние как происходящие под влиянием некоторых потоков событий. Потоком событий называется последовательность однородных событий, следующих одно за другим через какие-то, вообще говоря, случайные интервалы времени. Плотность вероятности перехода интерпретируется как интенсивность 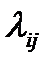соответствующих потоков. Если все потоки пуассоновские, то процесс будет марковским.

При изучении марковских случайных процессов с дискретными состояниями и непрерывным временем в графе состояний над стрелками, ведущими из состояния S_i в S_j проставляют соответствующие интенсивности 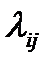.Такой граф состояний называют размеченным.

Пусть система S имеет конечное число состояний S₀, S₁,..., S_n. Случайный процесс, протекающий в этой системе, описывается вероятностями состояний Р₀ (t), P₁ (t),... Р_n (t), при этом:

.

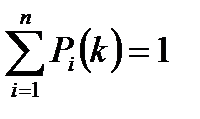Вероятности состояний P_i (t) находятся путём решения системы дифференциальных уравнений Колмогорова, имеющих вид:

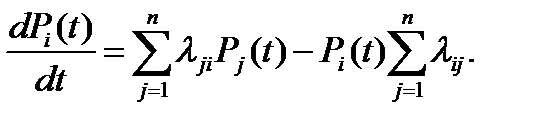
(2.3)

Уравнения составляют по размеченному графу состояний системы, пользуясь следующим мнемоническим правилом:

Производная вероятности каждого состояния равна сумме всех потоков ве­роятности, идущих из других состояний в данное состояние, минус сумма всех потоков вероятности, идущих из данного состояния в другие.

Например, для графа, изображённого на рис. 2.1, система уравнений Колмогороваимеет вид:

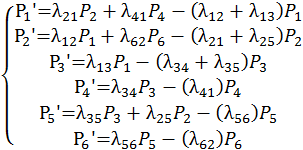. (2.4)

Чтобы решить систему дифференциальных уравнений, нужно знать начальное распределение вероятностей. Обычно для решения таких систем применяют численные методы (Рунге-Кутта) и решают их в специальных программных средах, например Mathcad имеет функцию rkfixed, реализующую эту процедуру.

2.4. Финальные вероятности состояний

Если процесс, протекающий в системе, длится достаточно дол­го, то имеет смысл говорить о предельном поведении вероятностей P_i (t) при .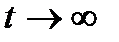

В некоторых случаях существуют финальные (предельные) вероятности состояний, независящие от того, в каком состоянии система S находилась в начальный момент. Говорят, что в системе S устанавливается предельный стационарный режим, в ходе которого она переходит из состояния в состояние, но вероятности состояний Р_i уже не меняются. Система, для которой существуют финальные вероятности, называется эргодической, а соответствующий случайный процесс – эргодическим.

Финальные вероятности состояний(если они существуют) могут быть получены путём решения системы линейных алгебраических уравнений, которые получаются из дифференциальных уравнений Колмогорова. Действительно, в установившемся режиме P ₀ (t),…, P_n (t) становятся постоянными, а производная от const равна 0. При этом вероят­ностные функции состояний в правых частях уравнений (2.3) заменяются соответственно на неизвестные финальные вероятности Р₀, Р₁,..., Р_п.

Таким образом, для системы S с п + 1 состояниями получается си­стема п +1 линейных однородных алгебраических уравнений с п+1 неиз­вестными Р₀, P₁,..., Р_п, которые можно найти с точностью до про­извольного множителя. Для нахождения точного значения Р₀, Р₁,..., Р_п к уравнениям добавляют нормировочное условие Р₀ + P₁ +... + Р_п = 1, пользуясь которым можно выразить любую из веро­ятностей Р_i.