1. Число попарно неизоморфных неупорядоченных корневых деревьев с 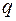 ребрами не превосходит числа упорядоченных корневых деревьев и, следовательно, не превосходит
ребрами не превосходит числа упорядоченных корневых деревьев и, следовательно, не превосходит 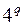 .
.
2. Число попарно неизоморфных деревьев с 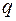 ребрами не превосходит числа корневых деревьев с
ребрами не превосходит числа корневых деревьев с 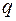 ребрами, так как они различаются выбором корневой вершины, следовательно, не превосходит
ребрами, так как они различаются выбором корневой вершины, следовательно, не превосходит 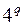 .
.
Пример 7. Деревья, приведенные на рис. 20, попарно изоморфны, но различны с точки зрения корневых деревьев.
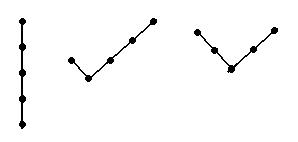 Рис. 20
Рис. 20
|
Задача о соединении городов. Пусть есть 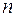 городов, расстояние между каждыми двумя городами известно. Надо соединить их дорогой минимальной длины (или минимальной стоимости, если известна цена дороги между каждыми двумя городами).
городов, расстояние между каждыми двумя городами известно. Надо соединить их дорогой минимальной длины (или минимальной стоимости, если известна цена дороги между каждыми двумя городами).
Эту задачу можно сформулировать на языке теории графов, полагая города вершинами, а расстояния – ребрами графа. Пусть каждому ребру графа поставлено в соответствие положительное число 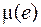 , называемое мерой ребра (расстояние между городами или стоимость прокладываемой дороги). Обозначим меру графа
, называемое мерой ребра (расстояние между городами или стоимость прокладываемой дороги). Обозначим меру графа 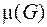
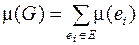 .
.
Стоит следующая задача: дан простой полный граф на 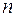 вершинах, задана мера каждого ребра, надо построить связный подграф минимальной меры. (Требование полноты исходного графа необязательно, достаточно, чтобы он был связным). Очевидно, что минимальный связный граф – дерево, поэтому задачу можно уточнить: построить остовное дерево минимальной меры.
вершинах, задана мера каждого ребра, надо построить связный подграф минимальной меры. (Требование полноты исходного графа необязательно, достаточно, чтобы он был связным). Очевидно, что минимальный связный граф – дерево, поэтому задачу можно уточнить: построить остовное дерево минимальной меры.
Алгоритм Краскала построения остовного дерева минимальной меры.
Выберем ребро минимальной меры, обозначим его 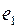 . Если несколько ребер имеют одну и ту же меру, берем любое. Затем выбираем ребро минимальной меры из оставшихся, обозначим его
. Если несколько ребер имеют одну и ту же меру, берем любое. Затем выбираем ребро минимальной меры из оставшихся, обозначим его 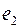 . Затем выбираем ребро минимальной меры из оставшихся, но так чтобы оно не образовывало цикла с выбранными ранее ребрами. Выбрав таким образом
. Затем выбираем ребро минимальной меры из оставшихся, но так чтобы оно не образовывало цикла с выбранными ранее ребрами. Выбрав таким образом 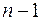 ребро, получим остовное дерево
ребро, получим остовное дерево 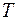 , причем
, причем
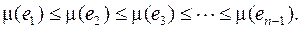
Покажем, что не будет остовных деревьев с мерой меньшей, чем мера дерева 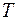 .
.
Пусть есть остовное дерево 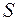 такое, что
такое, что 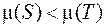 . Пусть
. Пусть 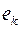 – первое ребро из
– первое ребро из 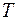 , не вошедшее в
, не вошедшее в 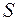 . Рассмотрим граф
. Рассмотрим граф 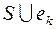 , он не является деревом, следовательно, в нем существует цикл
, он не является деревом, следовательно, в нем существует цикл 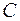 . Пусть
. Пусть 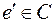 и
и 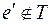 , такое ребро существует, так как
, такое ребро существует, так как 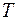 – дерево и не содержит циклов, удалив это ребро из графа
– дерево и не содержит циклов, удалив это ребро из графа 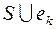 , получим граф
, получим граф 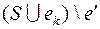 , он связный граф, в нем
, он связный граф, в нем 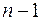 ребро, следовательно, он дерево. При этом графы
ребро, следовательно, он дерево. При этом графы 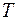 и
и 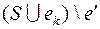 содержат на одно общее ребро больше, чем графы
содержат на одно общее ребро больше, чем графы 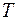 и
и 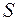 .
.
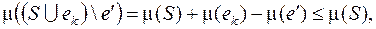
так как 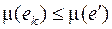 , иначе при построении дерева
, иначе при построении дерева 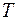 по алгоритму Краскала мы вместо ребра
по алгоритму Краскала мы вместо ребра 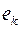 взяли бы ребро
взяли бы ребро 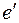 (ребра
(ребра 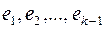 ) у деревьев
) у деревьев 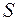 и
и 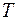 общие и
общие и 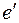 не образует с ними цикла).
не образует с ними цикла).
Пусть 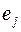 следующее ребро из
следующее ребро из 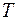 , не вошедшее в
, не вошедшее в 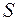 . Присоединим его к графу
. Присоединим его к графу 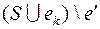 , вновь образуется цикл, удалим из него ребро
, вновь образуется цикл, удалим из него ребро 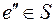 и
и 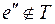 . Получим граф
. Получим граф 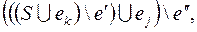 этот граф и граф
этот граф и граф 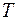 будут иметь на 2 общих ребра больше, чем графы
будут иметь на 2 общих ребра больше, чем графы 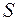 и
и 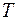 , при этом
, при этом 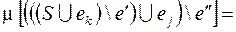
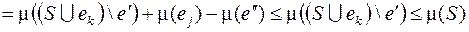 . Повторив эту процедуру конечное число раз, перестроим граф
. Повторив эту процедуру конечное число раз, перестроим граф 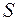 в
в 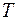 и получим противоречие
и получим противоречие 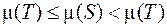 .
.
Пример 8. Найти остовное дерево минимальной меры в графе (рис. 21). Дерево, построенное по алгоритму Краскала, показано на рис. 22.
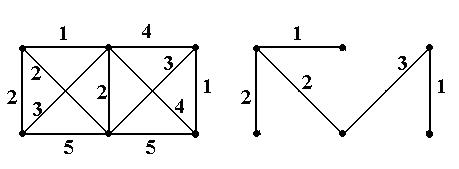 Рис. 21 Рис. 22
Рис. 21 Рис. 22
|
Определение. Циклическим рангом связного графа (или цикломатическим числом) 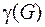 называют число ребер, которые необходимо убрать, чтобы граф стал деревом.
называют число ребер, которые необходимо убрать, чтобы граф стал деревом.
Если 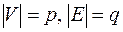 и так как в дереве число ребер
и так как в дереве число ребер 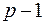 , то
, то 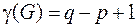 .
.
 2015-05-20
2015-05-20 1006
1006








