Энтропия объекта с дискретным распределением состояний

Рассмотрим объект, имеющий n случайных состояний S ₁, S ₂,..., S_n с вероятностями Р (S ₁), P (S ₂),..., P (S_n). Если одно из состояний объекта обязательно реализуется, а два состояния одновременно невозможны (полная группа несовместных событий), то

.

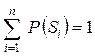Именно такие объекты в дальнейшем и рассматриваются.

Степень неопределенности состояний объекта зависит от числа n возможных состояний. Например, при бросании монеты их может быть только два, при бросании кубика - шесть. Степень неопределенности состояния объекта возрастает с увеличением n. Однако не только число возможных состояний определяет энтропию объекта. Например, если объект имеет шесть возможных состояний с вероятностями P (S ₁) = 0,95, P (S ₂) = P (S ₃) = P (S ₄) = P (S ₅) = P (S ₆) = 0,01, то с большой достоверностью можно утверждать априори, что он находится в состоянии S ₁, неопределенность состояния такого объекта невелика. Если же P (S ₁) = 1, а вероятности остальных состояний равны нулю, то объект вовсе не обладает неопределенностью - энтропия такого объекта равна нулю.

В теории информации энтропия - степень неопределенности состояния объекта, имеющего n возможных состояний с вероятностями Р (S ₁), P (S ₂),..., P (S_n), определяется выражением

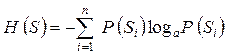. (4.23)

Параметр Н (S), введенный Шенноном в 1948 году, называется в теории информации энтропией объекта. Обозначение Н (S) показывает, что энтропия относится к объекту S, его не следует понимать как обозначение функциональной зависимости. Логарифм в формуле (4.23) может быть взят при любом основании, изменение основания приводит только к появлению множителя перед знаком суммы, т.е. к изменению единицы измерения. Наименование этой единицы зависит от выбора основания логарифма при вычислении энтропии: при выборе основания а = 2 единица измерения информации – бит, при а = 10 – дит, при использовании натуральных логарифмов – нит.

Исходя из соображений физической наглядности, будем вычислять энтропию объекта с использованием двоичных логарифмов; тогда

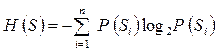. (4.24)

Целесообразность использования двоичных логарифмов легко понять, вычисляя энтропию объекта, имеющего два равновероятных состояния. В этом случае P (S ₁) = P (S ₂) = 0,5. По формуле (4.24) находим:

.

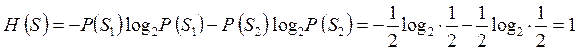Таким образом, за единицу измерения энтропии при выборе двоичных логарифмов принимается степень неопределенности объекта, имеющего два возможных равновероятных состояния. Эта единица измерения называется двоичной единицей или битом.

Если принять при вычислении энтропии десятичные логарифмы, то в качестве единицы информации использовалась бы неопределенность объекта, имеющего десять равновероятных состояний, т.е.

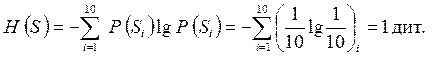
Поскольку в двоичных логарифмах

то отсюда следует, что 1 дит = 3,3 бит, а 1 бит = 0,302 дит.

Рассмотрим основные свойства энтропии.

1. Энтропия объекта есть величина вещественная и неотрицательная, так как 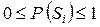, то .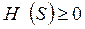

2. Энтропия объекта равна нулю в том крайнем случае, когда одно из возможных состояний S_n имеет вероятность P (S_n) = 1, т.е.

H (S) = 0 при P (S_n) = 1. (4.25)

Действительно, в формуле (4.24) слагаемое 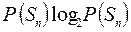равно нулю, так как 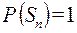. Другие слагаемые имеют неопределенные значения типа 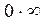, но можно показать, что 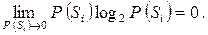В справедливости этого равенства можно убедиться на следующем примере. Пусть P (S_i) = 0,5 m, где m - большое число. Тогда

.

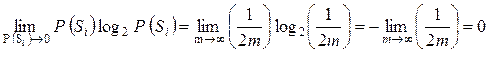Условие (4.25) следует для рассматриваемого объекта также из физических соображений, так как при P (S_n) = 1 о состоянии объекта известно достоверно заранее, поэтому в объекте нет никакой неопределенности.

3. Энтропия объекта с одинаковыми вероятностями состояний максимальна и равна логарифму числа состояний. Действительно, пусть P (S_i) = =1/ n, тогда по формуле для энтропии объекта (4.24) находим

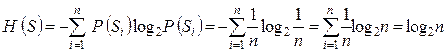. (4.26)

Пример 4.2. Пусть имеется объект с двумя возможными состояниями (бинарный объект). Вероятность первого состояния равна Р, тогда вероятность второго состояния из условия 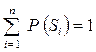равна 1 - Р. Определим энтропию этого объекта для следующих случаев:

а) состояния объектов равновероятны, т.е. Р ₁ = Р ₂ = 0,5; Р ₁ + Р ₂ = 1. Из формулы (4.24) получаем:

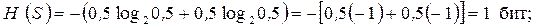
б) неравновероятные состояния. Пусть Р ₁ = 0,9; Р ₂ = 0,1; Р ₁+ Р ₂ = 1. Тогда

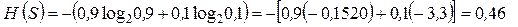бит;

в) детерминированные состояния. Р ₁ = 1; Р ₂ = 0; Р ₁ + Р ₂ = 1:

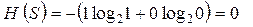бит.

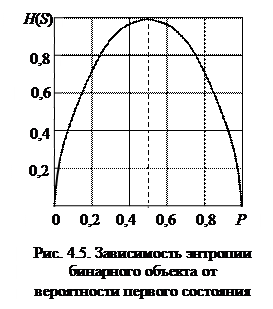
Изменение энтропии бинарного объекта в зависимости от вероятности P (S_i) показано на рис. 4.5, из которого видно, что максимум Н (S) = 1 достигается при Р ₁ = Р ₂ = 0,5, т.е. когда состояния равновероятны. При вероятностях Р = 0 или Р = 1, что соответствует полной невозможности или полной достоверности одного из состояний, энтропия равна нулю.