2015-05-20
766
Для решения системы итерационными методами преобразуем систему от формы (3.1) к виду [5]:
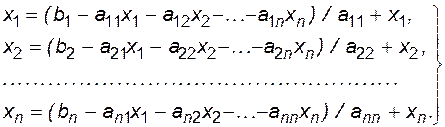(3.11)
Задав столбец начальных приближений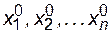 
, подставим его в правую часть системы (3.11) и вычислим новые приближения 
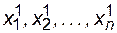, которые опять подставим в систему (3.11). Таким образом, организуется итерационный процесс, являющийся обобщением метода простых итераций на системы уравнений:
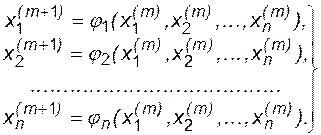(3.12)
Процесс (3.12) можно изменить, если использовать приближения к решениям, найденные при выполнении текущей итерации. Данное изменение известно как метод Зейделя [1] и, как правило, приводит к ускорению сходимости:
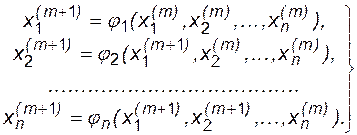(3.13)
Для сходимости итерационных методов необходимо, чтобы значения диагональных элементов матрицы А системы были преобладающими по абсолютной величине над другими элементами матрицы. Условия сходимости можно обеспечить преобразованием исходной матрицы путем перестановки уравнений и неизвестных.
Методы простых итераций и Зейделя можно применять и к решению систем нелинейных уравнений.
Условием окончания итерационного процесса является:
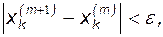(3.14)
где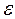 
- заданная погрешность; k - 1,2,3,... n.
