Алгоритм квадратных корней

Ввод: целое число n > 2.

Вывод: целая часть квадратного корня из n.

Шаг 1. Начинаем с присвоений: X = n и У = [(n + 1)/2] и переходим к шагу 2.

Шаг 2. Если X = У, то останавливаемся и выписываем Х; в противном случае переходим к шагу 3.

Шаг 3. Заменяем значение X на текущее значение У, а переменной Y присваиваем значение [(X² + n) / 2Х] и возвращаемся к шагу 2.

Модульное возведение в степень A^B mod n

Предположим, что даны три натуральных числа а, е и n. Опишем алгоритм определения вычета степе­ни а^е по модулю n. Для более эффективной работы алгоритма полезно представить показатель е в двоичной системе счисле­ния:

где коэффициенты 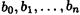могут принимать значения 0 или 1. Таким образом,

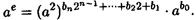
Заметим, что 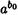может быть равно 1 (если b_о = 0) или а (если b_о = 1). Обозначив 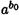через P₁, получаем

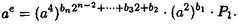
Теперь положим 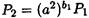. Тогда

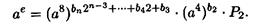
Продолжая начатую процедуру, мы определяем последователь­ность целых чисел 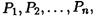где 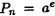. Конечно, поскольку мы делаем вычисления с элементами из Z_n, нам надлежит находить вычет всех произведений по модулю n на ка­ждом шаге алгоритма.

Обратите внимание на то, что на каждом этапе мы ли­бо возводим в квадрат число, либо вычисляем произведение 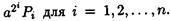Более того, если на каком-то шаге нам попалось нулевое значение b_i, нам совершенно не нужно вычислять .

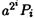На практике представление показателя е в двоичной си­стеме счисления происходит одновременно с вычислением сте­пени. Так, например, если е нечетно, то b_о = 1, в противном случае, b_о = 0. Аналогично, основываясь на четности или не­четности числа

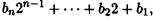
можно определить значение b₁. Заметьте, что выписанная сум­ма равна одному из следующих отношений: е / 2, если е — чет­но, и (е - 1) / 2, если оно нечетно. Формализованный алгоритм выглядит следующим образом: