1.10.2.1. РОМБИЧЕСКАЯ СИНГОНИЯ
Пример 1. Форстерит Mg2SiO4. Рис. 14.
По модели или по рисункам определяем симметрию. Находим три взаимно перпендикулярные оси второго порядка, три плоскости симметрии и центр инверсии: 3L23PC.
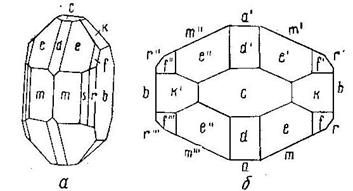
Рис. 16. Кристалл форстерита
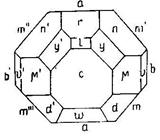
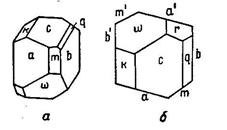
Модель кристалла форстерита состоит из десяти простых форм: три пинакоида, пять ромбических призм и две ромбические дипирамиды. Обозначим грани буквами. Грани одной и той же простой формы обозначаются одной и той же буквой. Принято грани юго-восточного сектора обозначать буквами без значков, например m. В северо-восточном секторе над буквой справа ставится значок /, например m/;в северо- западном два значка и в юго-западном – три, соответственно m//, m///.
Выбираем установку: три оси второго порядка берем за оси координат. За единичную следует брать грань, пересекающую все три оси под косыми углами. Таких граней две: e и f (рис.16, a). Выбираем e за единичную, т.к.полюс ее нормали будет лежать ближе к центру, чем полюс грани f.
Какие из осей второго порядка выбрать за Х, Y и Z? Поставим кристалл так, чтобы на основной круг проекции попадало возможно большее число полюсов. Для этого за вертикальную ось выбираем ту, которая перпендикулярна к грани с. За Yвозьмем ось, нормальную к граням b и bI, а за X последнюю ось второго порядка, нормальную к граням а и аI.
|
|
|
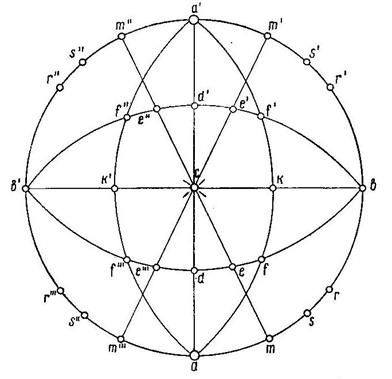
Рис.17. Проекция граней кристалла форстерита
Возьмем лист кальки размером около 23х24 см, кладем его на сетку и делаем центральную и боковую отметки. Вращаем кальку до тех пор, пока точки (отметки) не окажутся на одном и том же меридиане. Вращение надо делать совершенно свободно, не придерживая кальку в центре сетки и не скрепляя их булавкой или кнопкой. Только тогда точки окажутся приведенными на один меридиан, следует проверить, совпадает ли центральная отметка с центром сетки. Если нет, то меридиан найден неверно; тогда точно совмещают центры, отыскивают истинный меридиан и вновь проверяют центры. Иногда точки не укладываются ни на один из имеющихся на сетке кругов. Надо всегда помнить, что на сетке проведены лишь четные круги и между ними надо представить остальные с расстояниями примерно в 0,5о. Если точки не попадают на готовый круг, их надо помещать на одинаковые от него угловые расстояния, т.е. на один и тот же воображаемый меридиан.
В первую очередь наносим полюсы тех граней, которые могут быть нанесены без всяких углов, - это грани трех пинакоидов: с будет лежать в центре, а и в на основном круге проекции в точках пересечения с ним вертикального и горизонтального диаметров сетки.
Нам даны следующие углы mm/// =49o51/, ss/ =94o11/, rr / =71o18/, с е = 54о15/ и ff/// = 72o07/. Т.к. угол mm/// нам известен, можем нанести полюсы всех четырех граней m, так как вертикальная плоскость симметрии делит этот угол пополам. Следовательно, разделив 49o51/ на 2 получим половинный угол, округляя его до 25о, отложим его от точки а вправо и влево по основному кругу и наметим полюсы mm///. Такими же отсчетами находим сверху m/ и m//.
|
|
|
Аналогичным построением, используя данные углы ss/ =94o11/, rr / =71o18/, отсчитываем по основному кругу от точек в и в / половинные углы, т.е 47о и 35 1/2о, находим полюсы граней простых форм s и r.
Из рис. 16 б видим, что ребра между гранями m, e, c, e//, m// параллельны, следовательно, все эти грани лежат в одном поясе. Полюсы четырех граней m и грани с уже нанесены на проекцию, поэтому мы можем начертить оба пояса: mcm// и m///cm/. Точно так же мы можем провести пояса bcb/ и aca/, т.к. нам известны по три точки для каждого из этих поясов.
Теперь на поясе mcm// мы можем найти проекцию грани е, т.к. нам дан угол с е = 54о15/. Поворачиваем кальку так, чтобы полюсы граней m и m// совместились соответственно с нижним и верхним концами вертикального диаметра. Точка с должна при этом попасть в центр сетки. Отсчитывая по 54 1/4о вверх и вниз от точки с, находим полюсы граней е// и е. Проделав такую же работу с поясом m///cm/, находим проекции граней е ///и е /.
Все данные в задаче углы нами использованы, кроме угла ff/// = 72o07/. Как применить этот угол для нахождения проекций граней простой формы? Рассмотрим рис.1, b – ортогональную проекцию форстерита, видим, что ребра между гранями b, f, e, d, e///, f///, b/ параллельны; следовательно, все эти грани лежат в одном поясе. Проводим его, положив кальку так, чтобы точки b и b / совпали с концами вертикального диаметра, и прочеркиваем этот пояс, а также пояс bf/d/e//f//b/. Надо помнить, что пояса проектируются в виде больших кругов и чертить их можно только по меридианам, а не по параллельным кругам сетки.
Теперь можем нанести проекции всех четырех граней формы f. Нам дан угол ff/// = 72o07/. Мы видим, что плоскость симметрии, совпадающая при данном положении кальки с горизонтальным диаметром сетки, делит этот угол пополам. Отложим на проведенных поясах от горизонтального диаметра по половине угла 72o07/ , т.е. по 36о, найдем все четыре точки f /. Точки пересечения проведенных поясов с горизонтальным диаметром дадут нам проекции граней d и d /, т.к. они лежат в точках пересечения поясов bfede///f///b/ и adcd/a/.
Нахождение проекций граней при помощи точек пересечения поясов является очень удобным и часто применяемым способом. Таким образом, можем найти проекции граней ромбической призмы k. Из ортогональной проекции видно, что k лежит в точке пересечения bkck/b/ и fkf/. Проводим пояс ff/, найдем в точке его пересечения с горизонтальным диаметром (калька повернута в начальное положение) точку k и, соответственно, с левой стороны k / после проведения пояса f///f//.
Построение проекции форстерита закончено и можем приступить к графическому вычислению констант кристалла и символов его граней. Наметим точки выхода осей координат на проекции. В точках а и а / будет выходить ось Х; в а – ее положительный конец, в а / – отрицательный (соответственно в b и b / будут выходить +Y и -Y; в точке с будет выходить +Z. Углы между этими точками дадут осевые углы: +Z-Y= α, +Z-Х= β, +Х-Y= угол γ. В нашем случае все они равны 90о, как и полагается для кристалла ромбической сингонии. Единичная грань е дает возможность вычислить отношение а: в: с. Измеряем по дугам больших кругов, т.е. по меридианам сетки углы е +Х, е +Y и е +Z. Для этого ставит в южный полюс сетки +Х и, отсчитав дугу до е, получим 42о30 /. Проводим в южный полюс точку +Y, получим е +Y=70o. Для того, чтобы измерить угол е +Z, приводим е на один из диаметров сетки и по нему отсчитываем е +Z=54о15 /. Этот угол можно было бы и не измерять, т.к. он входит в число данных в задаче.
|
|
|
Теперь на основании формулы:
a: b: c = cosPoy / cosPox: 1: cosPoy / cosPoz
Можем написать a: b: c = 1/cos ex: 1/cosey: 1/cosez.
Поскольку отношение по оси Y принято приравнивать к единице, получим:
а: 1: с = соs ey / cos ex: 1: соs ey / cos ez = cos 70o / cos 42o30/: 1: cos 70o / cos 54o15/.
Находим в таблицах соответствующие значения косинусов:
Приводить отношения осевых единиц для минералов дальше четвертого знака не имеет смысла; данные, получаемые при измерении кристаллов на гониометре, не дает возможность получить более точные величины. Расхождения в вышеприведенных цифрах, взятых из надежных справочников, является характерным примером.
Геометрические константы форстерита получены, остается вычислить символы граней его простых форм. Для этого измеряем углы между полюсами всех граней и точками выхода осей координат на проекции. Заполняем первые три столбца таблицы № 6. Для каждой простой формы, входящей в комбинацию, достаточно найти символ одной из ее граней, так как для остальных граней этой простой формы символы будут состоять из тех же индексов. Изменяться будут только знаки и порядок расстановки индексов.
Таблица 8.
Вычисление символов граней форстерита
| Грани | Углы с осями | Косинусы углов | Частные cos P cos (111) | Cим-волы грани | ||||||
| + Х | + Y | + Z | + Х | + Y | + Z | + Х | + Y | + Z | ||
| a | 0o | 90o | 90o | - | - | - | (100) | |||
| b | 90o | 0o | 90o | - | - | - | (010) | |||
| c | 90o | 90o | 0o | - | - | - | (001) | |||
| m | 25o | 65o | 90o | 0,906 | 0,423 | 1,1 | 1,2 | (110) | ||
| s | 43o | 47o | 90o | 0,731 | 0,682 | (120) | ||||
| r | 54o30/ | 35o30/ | 90o | 0,581 | 0,814 | 0,8 | 2,4 | (130) | ||
| d | 39o | 90o | 51o | 0,777 | 0,629 | 1,1 | (101) | |||
| k | 90o | 40o30/ | 49o30/ | 0,760 | 0,649 | 2,2 | 1,1 | (021) | ||
| e | 42o30/ | 70o | 54o15/ | 0,737 | 0,342 | 0,584 | (111) | |||
| f | 51o | 54o30/ | 60o | 0,629 | 0,581 | 0,500 | 0,9 | 1,7 | 0,9 | (121) |
Формула h: k: l = cosP1x: cosP1y: cosP1z показывает, что для определения CosP0x cosP0y cosP0z
символа грани надо:
1) измерить углы, образуемые ее нормалью с тремя направлениями, выбранными за кристаллографические оси;
2) взять косинусы этих углов и разделить их на косинусы соответствующих углов той грани, которая выбрана за единичную.
Индексы символа при обозначении грани или простой формы пишутся подряд и берутся в круглые скобки. При этом на первое место ставится индекс по оси Х, на второе – индекс по оси Y и на третье – индекс по оси Z.
|
|
|
Для нахождения индекса грани по данной оси следует косинус угла, который составляет нормаль к этой грани с этой осью, разделить на косинус такого же угла для единичной грани.
Выписываем косинусы всех измеренных нами углов и составляем 5-7 столбцы таблицы. Затем производим указанное в формуле деление и получаем столбцы 8-10. Деление достаточно вести до первого знака, в редких случаях до второго. Отношения полученных дробей (правильных и неправильных) приводим к отношению целых чисел. Так как мы делали вычисление графически, полученные нами цифры являются приближенными, но индексы всегда должны быть целыми числами. Например, для грани ромбической призмы m мы получили 1,1: 1,2: 0; первые две цифры можно считать равными и написать символ (110). Для ромбической дипирамиды f имеем 0,9: 1,7: 0,9; можно считать, что 0,9 в два раза меньше 1,7, и поэтому символ этой формы будет (121).
Для тех граней, у которых в таблице косинусов имеются два нуля, например 1: 0: 0, никакого деления на косинус единичной грани делать не надо, а сразу написать символ (100). Если произвести указанное деление, то в столбцах 8-10 для формы а получим 1,3: 0: 0. Для того, чтобы это отношение привести к отношению целых чисел, все три члена отношения нужно разделить на 1,3 и получить 1: 0: 0. Следовательно, для таких граней, как а, b, с, никакого деления на косинусы единичной грани делать не надо.
Суммируем результаты нашей работы в виде следующей характеристики минерала форстерита (Mg2SiO4):
1. 3L23PC
2.Низшая категория. Ромбическая сингония. Планаксиальный вид.
3.Отношение осевых единиц а: b: с = 0,4649: 1: 0,5854.
4.Простые формы:
а) пинакоид; {100}
b) пинакоид;{ 010}
с) пинакоид; {001}
m) ромбическая призма {110}
s) ромбическая призма {120}
r) ромбическая призма {130}
d) ромбическая призма {101}
k) ромбическая призма {021}
e) ромбическая дипирамида {111}
f) ромбическая дипирамида{121}
Расставляем на стереографической проекции символы всех граней. Все значения заносятся в таблицу.
1.10.2.2. МОНОКЛИННАЯ СИНГОНИЯ
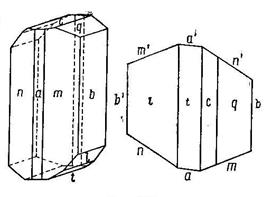
Пример 2. Ортоклаз КАlSi3O8 (Рис. 16, а и b)
По модели или рисунку определяем симметрию: плоскость симметрии, ось второго порядка и центр инверсии. Следовательно, кристалл относится к низшей категории, моноклинной сингонии, планаксиальному виду: L2PC.
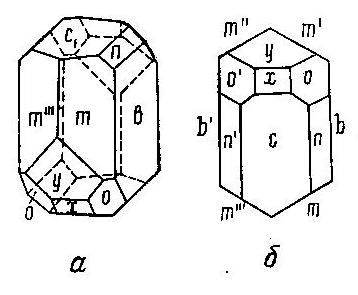
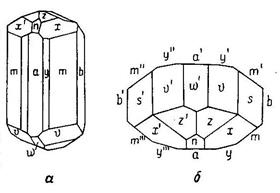
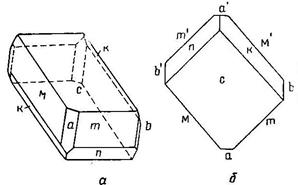
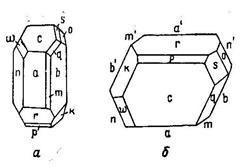
Рис. 18. Кристалл ортоклаза; а) вид сбоку, б) вид сверху
Простые формы: b) пинакоид; с) пинакоид; х) пинакоид; у) пинакоид;
m) ромбическая призма; n) ромбическая призма; о) ромбическая призма.
Берем лист кальки и кладем его на стереографическую сетку. Намечаем центр и обводим по сетке основной круг проекции (рис.19). Ориентируем кристалл так, чтобы пояс mbm/m// и т.д. принял вертикальное положение. Если будем смотреть на кристалл сверху, то увидим картину, данную на рис.18b. Нанесем на проекцию элементы симметрии. Выходы оси второго порядка, как совпадающей с нормалями к граням b, b/, попадут на основной круг проекции. Мы можем поместить их на две любые диаметрально противоположные точки основного круга. Наметим b и b/ на крайних точках экватора сетки справа и слева (рис.17). Плоскость симметрии изобразится диаметром, соединяющим оба полюса сетки. Наносим этот диаметр на кальку.
Измеряем углы гониометром и сверяем их с величинами, взятыми из справочника. Рассмотрим полученную таблицу углов:
mm/// = 61o (61o13/), cm = 68o (67o47/), с х = 50о (50о16/), с у = 80о (80о18/),
с n =45о (44о56/), х о = 27о (26о52/).
Проще всего наносятся грани m, так как мы знаем, что они лежат на основном круге и угол между двумя гранями m нам известен. Далее найдем грани с, х и у, лежащие перпендикулярно к плоскости симметрии, и, наконец, оставшиеся грани n и о.
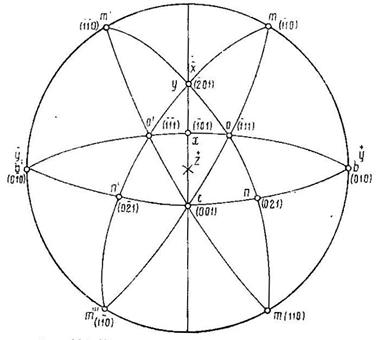
Рис. 19. Проекция граней кристалла ортоклаза
Грани m и m/// расположены симметрично относительно плоскости симметрии, следовательно, она делит пополам угол между обеими гранями, так как углы даются всегда между нормалями.
Берем половину угла 61o13/, т.е.приблизительно 30 1/2о, отсчитываем эту величину вправо от нижнего полюса сетки (где основной круг пересекает плоскость симметрии) по основному кругу и находим проекцию грани m. Сделав такой же отсчет влево, найдем m///. От верхнего полюса строим m/ и m//.
При работе с 10-сантиметровой сеткой для получения более точных отсчетов рекомендуется пользоваться лупой с увеличением 4-6 раз.
Теперь весь вертикальный пояс нанесен и даст нам опорные пункты для дальнейшего проектирования.
Обычно все грани на кристалле расположены по поясам или зонам. Поясом называется совокупность граней, пересекающихся по параллельным ребрам; направление ребер, проведенное через начало координат, называется осью пояса. При этом всегда надо помнить:
1) Пояс всегда изображается на стереографической проекции в виде большого круга.
2) Как всякий большой круг на шаре, пояс определяется двумя точками при условии, что эти точки не представляют концов одного и того же диаметра.
3) Полюсы пояса или выходы его оси являются полюсами большого круга, изображающего этот пояс на проекции.
4) Если какая-либо грань принадлежит одновременно двум различным поясам, то проекция этой грани определяется точкой пересечения этих поясов.
Какие зоны или пояса наблюдаются на примере ортоклаза? Ищем на рисунках параллельные ребра и находим несколько поясов: сху; bncn/b/, boxo/b/ … и т.д. Выбираем тот из них, который проще всего связывается с нанесенными уже точками. Это будет пояс сху; ось его совпадает с осью L2, полюсы будут лежать в точках b и b/. Следовательно, нормали к граням этого пояса должны лежать в плоскости симметрии, отсюда cледует, что проекции их попадут на диаметр, изображающий эту плоскость. Этот же диаметр будет проекцией пояса сху.
Нанесем его грани. Положение всякой точки на сфере определяется пересечением двух дуг. Одна дуга (изображенная на проекции диаметром) у нас есть. Для построения каждой из точек сх и у нам надо иметь еще одну дугу. Они даны углами mc, cx, cy. Справа мы должны найти грань с. Если нам дан угол mc = 67о47/, значит точка с лежит на малом круге, проведенном из m, радиус которого равен 67о47/.
Построение малых кругов значительно облегчается тем, что точка m лежит на основном круге проекции. Приведя ее в полюс сетки и отсчитав 67о47/, обводим часть соответствующей параллели до встречи с диаметром. Точка пересечения будет искомой проекцией грани с. От нее не трудно найти х и у, так как угловые расстояния их от с нам известны; кроме того, мы знаем, что они лежат на проведенном уже диаметре. Отсчитываем от с вверх 50 и 80о и отмечаем точки х и у. Теперь нами закончен второй пояс, перпендикулярный первому (mbm/m// … и т.д.).
Найденные точки дают возможность провести несколько новых поясов и воспользоваться ими для нанесения оставшихся граней n и о. Проведя большой круг через точки b, c, b/, нанесем пояс, в котором лежит грань n (рис.16); зная расстояние от n до с из таблицы углов, легко найдем проекции граней n и n/. Проводим b и b/ в полюсы сетки и наносим круг bcb/ по меридиану. Затем отсчитываем от точки с 45о и отмечаем положение найденной таким образом грани. Симметрично наносим n/. Для нахождения проекции грани о делаем построение, аналогичное предыдущему. Грань о лежит в поясе boxo/ b/; проводим опять b и b/ в полюсы сетки и наносим меридиан, проходящий через точку х. Затем от х отсчитываем вверх и вниз 27о и находим о и о/.
Теперь нанесены все грани и задача проектирования закончена. Остается сделать проверку начерченной проекции. Из рисунков видим, что на кристалле имеются пояса, которыми мы не пользовались при построении и поэтому их не нанесли. Если теперь проведем некоторые из этих поясов и увидим, что нанесенные точки расположены на них и в точках их пересечения, то проекция построена верно.
Приводим m и m// в полюсы сетки. Проекции граней с и о должны оказаться на одном меридиане; равным образом точки n, о, у должны попасть на другой. Наносим эти пояса на проекцию и приводим в полюсы сетки грани m /// и m /. Теперь наносим пояса m///n/o/ym / и m///com/. Если около точек с о о/ и у не получается треугольников от пересечения начерченных дуг, то проекция сделана верно; если такие треугольники имеются, то где-нибудь есть ошибки в отсчетах.
Рассмотрим теперь, каким образом можем определить константы элементарного параллелепипеда решетки, исходя из построенной нами стереографической проекции кристалла.
1. Следует взять три ряда решетки, которые будут служить ребрами параллелепипеда.
2. Надо найти грань, пересекающую эти три ряда. Отрезки, которые эта грань отсечет на рядах, дадут возможность построить параллелепипед. Это и будет та грань, которую мы назвали единичной.
На этом примере выбираем за оси координат следующие направления: за ось Х направление ребер пояса bncn/b/, за ось Y – L2, т.е. направление ребер пояса с х у, и за ось Z– направление ребер пояса mbm/m//.
За ось координат берем направление ребра, т.е. мы берем направление в решетке, параллельное этому ребру, и следовательно всем ребрам определенного пояса. Это направление и будет осью пояса, оно будет выходить в полюсе того большого круга, который соответствует данному поясу на проекции.
Следовательно, когда хотим найти на проекции направление оси какого либо пояса (или серии параллельных ребер на кристалле), то должны взять полюс того большого круга, который изображает этот пояс на проекции.
В данном случае (в ортоклазе) ось Х проектируется в полюсе пояса bncn/b/, ось Y – в полюсе пояса с х у и ось Z–в полюсе пояса mbm/m// …, т.е. в центре основного круга. Положительным направлением считается: для оси Х – к наблюдателю, для оси Y – вправо и для оси Z – вверх. Следовательно, на рис.4 мы имеем +Z, +Y и –Х, положительный конец оси Х оказался под плоскостью проекции и попал в нижнее полушарие.
Зная точки выхода осей, можно легко измерить осевые углы, т.е. углы между ребрами параллелепипеда, приводя эти точки на один меридиан. Проделав это, получим: угол +Z+Y = α=90о; угол = +Z-Х = 64о, следовательно, угол +Z+Х= β=180-64=116о и угол +Х+Y= γ= 90о.
Определим относительную величину ребер параллелепипеда. Для этого сначала выберем единичную грань. Какая из нанесенных на проекцию граней пересекает все три оси координат под косыми углами. Только грань о. Измерив углы между ее проекцией (о) и точками выхода осей, получим: 133, 63 и 36о; взяв косинусы этих углов и подставив в формулу, получим:
ОА:ОВ:ОС = а: b: с = 1: 1: 1
0,682 0,454 0,809
Или а: 1: с = 0,454: 1: 0,454 = 0,6658: 1: 0,5613.
0,682 0,809
Это значит, что если за ребро b взять например 10 см, то ребра а и с будут равны (округлая) 6,7 и 5,6 см, т.е. теперь мы можем построить искомый параллелепипед, т.к. знаем все его элементы.
Переходим к определению символов граней кристалла.
Из формулы h: k: l = cosP1x: cosP1y: cosP1z
CosP0 xcosP0 ycosP0z
видим, что для этого нам необходимо знать косинусы углов, которые нормали к граням образуют с точками выхода кристаллографических осей Х,Y и Zна проекции. Эти углы легко измерить при помощи сетки Вульфа, приводя полюс грани и точку выхода оси на один меридиан. Результаты измерения заносим в таблицу 9.
В столбце 1 таблицы пишем буквенные обозначения граней. В столбцах 2,3 и 4 располагаем соответствующие углы с осями +Х, +Y и +Z. В столбцах 5,6 и 7 выписываем косинусы измеренных углов. Зная эти косинусы, по формуле (4) на стр. 95 составляем столбцы 8,9 и 10. При этом принимаем в расчет знак делимого (например для косинусов граней о х и у), как в делителе берем только абсолютную величину косинуса единичной грани. Знак минус здесь не принимается во внимание, т.к. отрезки, отсекаемые единичной гранью, определяют масштабы по осям и как единицы меры не имеют знака.
Таблица 9
Вычисление символов граней ортоклаза
| Грани | Углы с осями | Косинусы углов | Частные cos P cos (111) | Cим-волы грани | ||||||
| + Х | + Y | + Z | + Х | + Y | + Z | + Х | + Y | + Z | ||
| b | 90o | 0o | 90o | - | - | - | (010) | |||
| c | 90o | 90o | 26o | 0,899 | - | - | - | (001) | ||
| m | 39o | 59o | 90o | 0,777 | 0,515 | 1,14 | 1,13 | (110) | ||
| n | 90o | 45o | 50o | 0,707 | 0,643 | 1,56 | 0,79 | (021) | ||
| о | 133o | 63o | 36o | -0,682 | 0,454 | 0,809 | -1 | (-111) | ||
| х | 141o | 90o | 24o | -0,777 | 0,914 | -1,14 | 1,13 | (-101) | ||
| y | 171o | 90o | 54o | -0,988 | 0,588 | -1,45 | 0,73 | (-201) |
Дробные отношения заменяем отношением целых чисел, делая при этом соответствующие сокращения. Например, для грани m имеем 1,14; 1,13 и 0. Первые две величины можем принять за равные и, разделив их одну на другую, получим 110 – это и будет символ грани, если его написать в виде (110).
Возьмем еще пример. Для грани у имеем 1,45; 0; 0,73. Без натяжки можем считать, что 0,73 по абсолютной величине вдвое меньше 1,45. Разделив все три величины на 0,73, получим -2, 0, 1 – символ (-201). Таким образом, составляем последний столбец таблицы 2.
Здесь, для символов ребер принято заключать индексы в квадратные скобки, например [100]. Фигурные скобки означают символ всей простой формы. Если в нашем примере для mпоставить {110}, то это будет обозначать всю простую форму – ромбическую призму, состоящую из граней (110), (-110), (1-10) и (-1-10). Знак минус (-) ставится в символе над соответствующим индексом; он показывает, что грань пересекает отрицательное направление оси (как на взятом примере грани о, х и у пересекают ось Х). Вписываем найденные индексы в соответствующих местах на проекции.
1.10.2.3. ТРИКЛИННАЯ СИНГОНИЯ
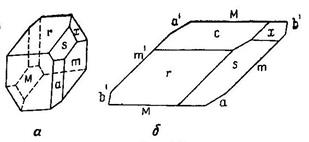
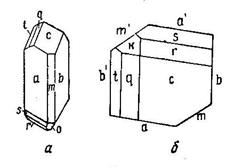
Пример.3. Борная кислота В(ОН)3, (рис. 18.)
Даны углы: bm =59o00/; mM =61o30/; cm = 80o33/; cs = 43o14/; cv = 41o06/; cM = 95o03/.
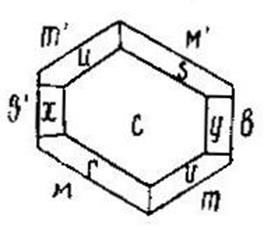
Рис. 20. Кристалл борной кислоты (вид сверху)
Из рис. 20 определяем, что кристалл принадлежит к низшей категории, триклинной сингонии, центральному виду: С.
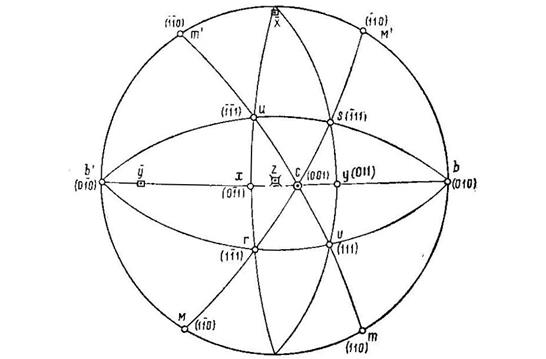
Рис. 21. Проекция граней кристалла борной кислоты
1.Ставим пояс Mmb … и т.д. вертикально (рис.21); помещаем b и b / по концам экватора, как делали в примере.
2.Грани m и M наносятся легко по имеющимся углам.
3.От них находим полюс грани с двумя засечками (80о30/ и 95о).
4.Проводим пояса mcm/ и McM /. На них находим s и v по их углам с гранью с.
Все данные исчерпаны, а осталось нанести целый ряд граней – х, у, u, r. Нам должны помочь имеющиеся пояса.
5.Проводим пояса bcb / и vs – в точке их пересечения лежит полюс грани у.
6.Проводим пояс bsb/. В точке пересечения его с поясом mcm лежит полюс грани u; проведя bvb/, найдем r в точке пересечения этого пояса с McM /.
7.Пояс ur в пересечении с bcb/ даст полюс грани х. Таким образом, используя каждую вновь получаемую грань, мы дошли до конца задачи.
За кристаллографические оси возьмем направления ребер следующих поясов:
для оси Х – ось пояса b/xcyb,
для оси Y– ось пояса, проходящего через с и опирающегося на точки пересечения поясов vys и r x u с основным кругом. В этих точках должны лежать грани пинакоида (100), который на кристаллах борной кислоты не наблюдается.
Для оси Z – ось пояса Mmb …, она выходит в центре проекции.
Наносим точки выходов осей координат. Для Х и Y имеем отрицательные концы. Измеряем осевые углы:
α = 104о; β = 93о; γ =89о20 /;
Сравним с величинами, полученными вычислением:
α = 104о17 /; β = 92о34 /; γ = 89о42 /.
За единичную грань принимаем v. Результаты графического вычисления приведены в таблице 8:
а: 1: с = 0,326: 1: 0,326 =0,5611: 1: 0.5284;
0,580 0,620
Таблица № 10
Вычисление символов граней борной кислоты
| Грани | Углы с осями | Косинусы углов | Частные cos P cos (111) | Cим-волы грани | ||||||
| + Х | + Y | + Z | + Х | + Y | + Z | + Х | + Y | + Z | ||
| c | 90o | 90o | 15o | 0,966 | - | - | - | (001) | ||
| b | 90o | 14o15/ | 90o | 0,970 | - | - | - | (010) | ||
| m | 31o | 60o | 90o | 0,857 | 0,500 | 1,5 | 1,5 | (110) | ||
| M | 30o40/ | 120o | 90o | 0,860 | -0,500 | 1,5 | -1,5 | (1-10) | ||
| y | 90o | 65o15/ | 38o45/ | 0,412 | 0,781 | 1,3 | 1,3 | (011) | ||
| х | 90o | 121o | 17o45/ | -0,515 | 0,953 | -1,6 | 1,5 | (0-11) | ||
| v | 54o30/ | 71o | 51o45/ | 0,580 | 0,326 | 0,620 | (111) | |||
| s | 127o | 71o | 50o45/ | -0,660 | 0,326 | 0,636 | -1,1 | (-111) | ||
| r | 50o | 112o | 46o | 0,642 | -0,375 | 0,696 | 1,1 | -1,2 | 1,1 | (1-11) |
| u | 130o30/ | 114o | 43o | -0,649 | -0,407 | 0,732 | -1,1 | -1,2 | 1,2 | (-1-11) |
Вычисленные величины: - 0,5771: 1: 0,5282;
Во всех разобранных примерах мы не испытали затруднений при определении отношения а: b: с и символов граней потому, что всегда имелась грань, пересекающая все три оси Х, Y и Z, которую можно было взять за единичную.
На практике часто случается, что ни одна грань измеренного кристалла (при определенной установке) не будет удовлетворять этому условию. Рассмотрим несколько вариантов.
1.Есть две грани, которые пересекают попарно все три оси; например, одна пересекает Х и Y, другая Yи Z. Приняв первую за (110), определяем а: b; из второй, принятой за (011). Находим b: с. Приравнивая эти отношения, получим искомое а: b: с.
При графическом вычислении можно решить эту задачу следующим образом. Проводим дуги (001) – (110) и (100) – (011). В точке пересечения этих дуг найдем место отсутствующей на кристалле грани (111).
2.Имеется одна грань, пересекающая две оси. В общем случае задачу решить нельзя; можно определить лишь одно из отношений а: b, b: с или а: с. В частных случаях полное вычисление кристалла возможно, а именно:
1)когда кристалл принадлежит к одной из средних сингоний и грань пересекает ось Zи одну из двух других;
2)когда кристалл принадлежит к кубической сингонии. В последнем случае безразлично, какие две оси пересекают грань.
3.Нет граней, пересекающих оси попарно. Это может быть в том случае, когда на кристалле имеются всего три пары параллельных граней (или четыре в случае гексагонального облика). Задачу решить нельзя. Можно, приписав граням символы (100), (010) и (001), измерить осевые углы, но а: b: с определить невозможно.
1.10.2. ПРИМЕРЫ ВЫПОЛНЕНИЯ РГР ДЛЯ МОДЕЛЕЙ СРЕДНЕЙ КАТЕГОРИИ
1.10.2.1. ТЕТРАГОНАЛЬНАЯ СИНГОНИЯ
В тетрагональной сингонии мы имеем три оси. За Z берется L4. За Х и Y оси второго порядка, нормали к плоскостям симметрии, или, направления действительных или возможных ребер (взаимно перпендикулярных, а также перпендикулярных к главной оси).
1.10.3.2. ГЕКСАГОНАЛЬНАЯ И ТРИГОНАЛЬНАЯ СИНГОНИИ
Во всех видах этих сингоний есть одна ось высшего порядка, ее всегда берут за вертикальную ось Z. Если есть оси второго порядка (всегда перпендикулярные к главной), то они берутся за три остальные оси, которые в этих сингониях называются Х, Y и U. Если таких сингоний нет, то есть плоскости симметрии, параллельные главной оси (например, в видах L66PL33P), то за Х, Y и U берут три нормали к этим плоскостям. Наконец, в видах, где нет ни осей L2, ни плоскостей, параллельных главной оси (например L6,L6PC, L3, L3P), за оси Х, Y и U берутся направления трех действительных или возможных ребер, удовлетворяющие поставленному условию (углы 120о), т.е. тому, что угол γ = 120о считается между одноименными выходами осей (плюс или минус).
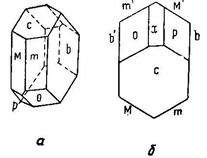
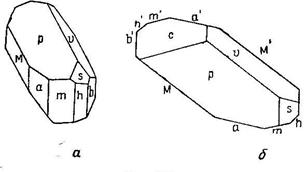
Пример: Кристалл гринокита (CdS). Определяем элементы симметрии: одна ось шестого порядка и шесть пересекающихся по ней плоскостей симметрии (L66P). Осей второго порядка нет, следовательно, за Х, Y и U придется брать нормали к плоскостям симметрии. Т.к. плоскостей симметрии шесть, то возможны две различные установки. Сначала возьмем ту, при которой ось Y является осью пояса mzxic и т.д.
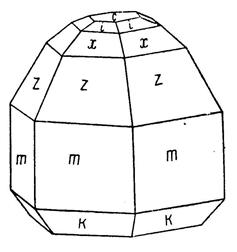
Рис. 22. Кристалл гринокита
Точка ее выхода будет в ребре между гранями m/ и m//. Тогда ось Х будет выходить в ребре между гранями mm V, а U – между гранями m/// и mIV. За ось Z, согласно правилам установки, берется ось L6. За единичную мы можем выбрать грань одной из трех гексагональных пирамид z, x и i. Неоднозначность установки сказывается здесь очень резко, т.к. в каждом случае символы будут различные. Сначала выберем за единичную грань формы х, как лежащую между z и i. Ее символ будет (1011), т.к. она параллельна оси Y. При этой установке грани гринокита получают следующие символы: с – (0001), m – (10-10), z – (20-21), i – (1012), k – (1011) и нижний моноэдр γ, не показанный на рисунке, - (0001).
Разберем второй вариант: за X, Y и U возьмем нормали к граням простой формы m, т.е. нормали к трем другим плоскостям симметрии кристалла гринокита. Тогда точка выхода оси Х будет совпадать с полюсом грани mV на проекции, Y будет совпадать с полюсом грани m/ и U с полюсом грани m///. За единичную возьмем грань гексагональной пирамиды х. При этой установке ее символ будет (1121). Другие грани получат следующие символы: m – (1120), z – (2241), i – (1122), c – (0001), k – (1121), γ – (000-1).
Других вариантов этой установки, т.е. тех, которые получаются при выборе за единичную граней z и i, рассматривать не будем, т.к. считаем, что вопрос рассмотрен достаточно детально.
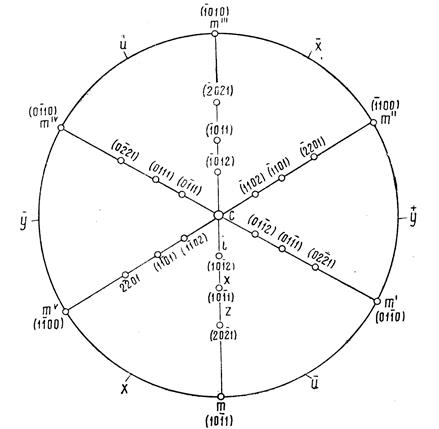
Рис.23. Стереографическая проекция кристалла гринокита.
В тригональной и гексагональной сингонии принята установка Бравэ, при которой сумма индексов по трем горизонтальным осям (Х,Y и U): h+i+k =0. Когда один из индексов равен 0, два другие должны быть разного знака и равны друг другу по абсолютной величине. Когда ни один из трех индексов не равен 0, то абсолютная величина одного из них должна быть равна сумме абсолютных величин двух других: k=h+i.
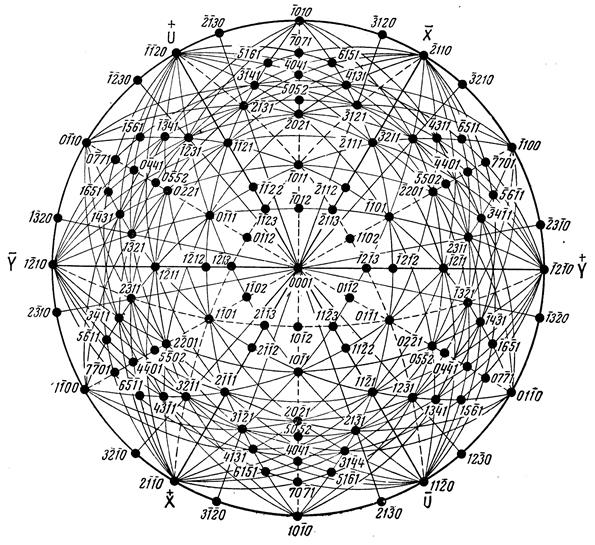
Рис.24. Комплекс граней в гексагональной сингонии
1.10.3. ПРИМЕРЫ ВЫПОЛНЕНИЯ РГР ДЛЯ МОДЕЛЕЙ
ВЫСШЕЙ КАТЕГОРИИ
1.10.3.1. КУБИЧЕСКАЯ СИНГОНИЯ
Во всех видах кубической сингонии есть три взаимно перпендикулярные оси симметрии: либо 3L4, либо 3L2. Они берутся за оси Х, Y иZ. Так как эти три оси симметрии совершенно одинаковы, то безразлично, какую именно поставить на то или другое место. За единичную грань берется грань октаэдра или тетраэдра.
Поскольку в кубической сингонии установка однозначна, углы между гранями различных простых форм этой сингонии также имеют постоянные определенные значения. Хотя при определении символа на глаз и нельзя точно указать составляющие символ индексы, все же для более точного их определения приведем таблицы, содержащие углы для простых форм с наиболее простыми символами.
Угол между гранями октаэдра (111) – (-111) = 70о31/
Угол между гранью октаэдра и куба (100) – (111) = 54о44/
Угол между гранью октаэдра и ромбододекаэдра (111) – (110) = 35о15/
Представим себе (рис.23.) на прекции грани (100), (010), (001) и (111) – основной тетраэдр. Проведя дуги больших кругов (001) – (111); (100) – (111); (010) – (111), найдем три точки их пересечения с дугами (100) – (001), (100) – (010) – (001); это будут точки d,m,e. Они являются полюсами возможных граней, так как представляют собой точки пересечения двух поясов. Символ грани m должен быть равен сумме индексов (100) и (010), т.е. должен иметь индексы (110). Проверяем по дуге (001) – m: сумма индексов m+(001) равна (111); следовательно, (111) минус (001), т.е. (110), есть символ грани m. Таким же способом найдем и проверим символы граней d=(101) и е=(011).
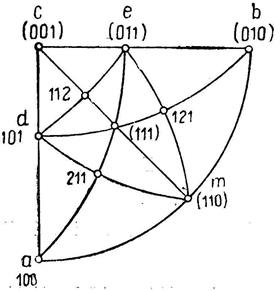
Рис.25. Нахождение символов грани суммированием индексов
Проведя диагонали сферических четырехугольников, например. (100) – (110) – (111) – (101), получим новые грани (211), (121) и (112). Обратим внимание на то, что все три символа сходны. В каждом по две единицы и одна двойка4 эта двойка меняет свое место: чем ближе проекция грани к выходу оси, тем выше индекс по этой оси. Шесть треугольников. На которые разбивается исходный треугольник (100) – (010) – (001), называются треугольниками первого периода.
Для продолжения построения необходимо для каждого из них найти центральную точку. Это делается проведением соответствующих дуг. Например, центральную точку для треугольника (100) – (101) – (111) найдем в точке пересечения дуг (101) – (110) и (100) – (112). Найдя центральную точку для треугольника первого периода, его можно разбить в свою очередь на шесть треугольников 2 периода и т.д. При индицировании вновь получающихся возможных граней надо идти последовательно по периодам, иначе могут получиться неправильные результаты. Это построение называется развитием комплекса граней по периодам.
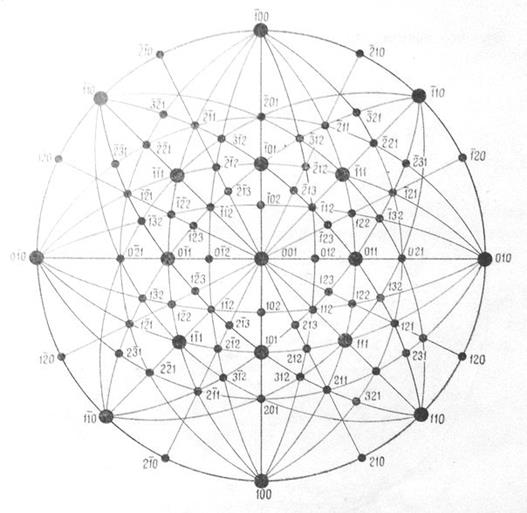
Рис. 26. Комплекс граней в кубической сингонии.
Отсюда ясно, что положения четырех исходных граней играют решающую роль в распределении всех остальных граней. Это вытекает из того факта, что основной тетраэдр определяется формой ячейки пространственной решетки, которая характеризует и внешнюю форму кристалла.
Варианты заданий РГР
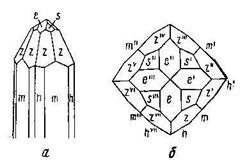
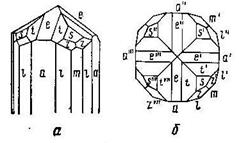
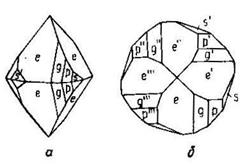
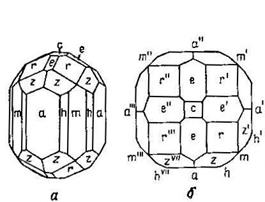
1.11.1.1. ТЕТРАГОНАЛЬНАЯ СИНГОНИЯ
| 
|
| 
|
| 
|
| 
|
| 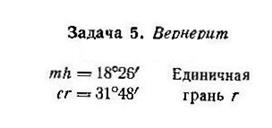
|
1.11.1.2. ТРИГОНАЛЬНАЯ И ГЕКСАГОНАЛЬНАЯ СИНГОНИЯ
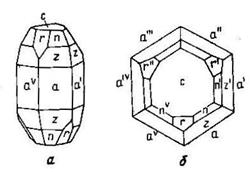
| 
|
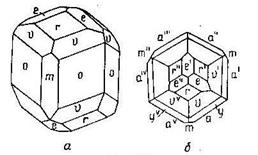
| 
|
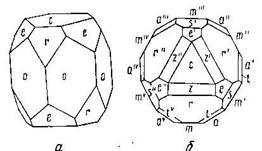
| 
|
| 
|
| 
|
| 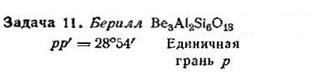
|
| 
|
| 
|
1.11.1.3. РОМБИЧЕСКАЯ СИНГОНИЯ
| 
|
| 
|
| 
|
| 
|
1.11.1.4. МОНОКЛИННАЯ СИНГОНИЯ
| 
|
| 
|
| 
|
| 
|
| 
|
1.11.1.5. ТРИКЛИННАЯ СИНГОНИЯ
| 
|
| 
|
| 
|
| 
|
| 
|
| 
|
| 
|
| 
|
 2015-05-12
2015-05-12 2592
2592
