Предельные теоремы Муавра - Лапласа. Теорема Пуассона

В настоящей главе мы изучим основные закономерности, относящиеся к одной из важнейших схем теории вероятностей – схеме последовательных независимых испытаний с двумя исходами. Подробное исследование таких испытаний имеет большое теоретическое и практическое значение.

Пусть многократно проводится некоторый эксперимент, в результате которого может произойти только событие А или противоположное ему событие ` А, причем вероятность появления события А в каждом эксперименте не зависит от результатов предыдущих испытаний и равна p (0 < p < 1). Тогда вероятность появления в каждом эксперименте противоположного события , очевидно, равна q = 1 -p. Такая схема проведения испытаний была впервые изучена Я. Бернулли и поэтому называется схемой Бернулли.

Допустим, что эксперимент проведен n раз. Вычислим вероятность 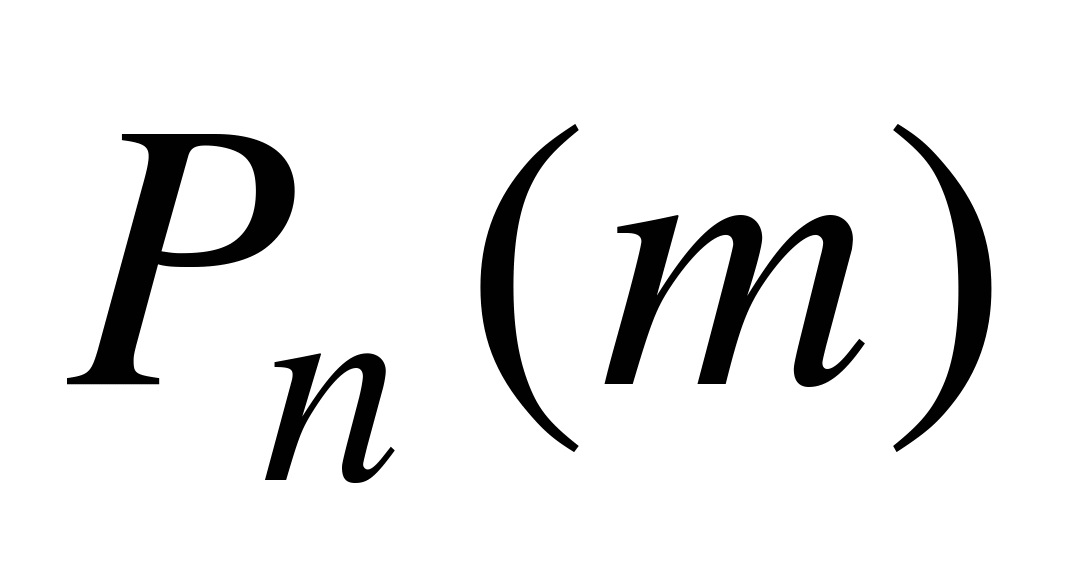того, что при n испытаниях событие А наступит ровно m раз (а остальные (n–m) раз наступит событие . Сначала выберем m испытаний из проведенных n и зафиксируем их номера. Вероятность того, что при этих m испытаниях произошло событие А, а в остальных (n–m) испытаниях - событие , согласно теореме умножения для независимых испытаний, равна .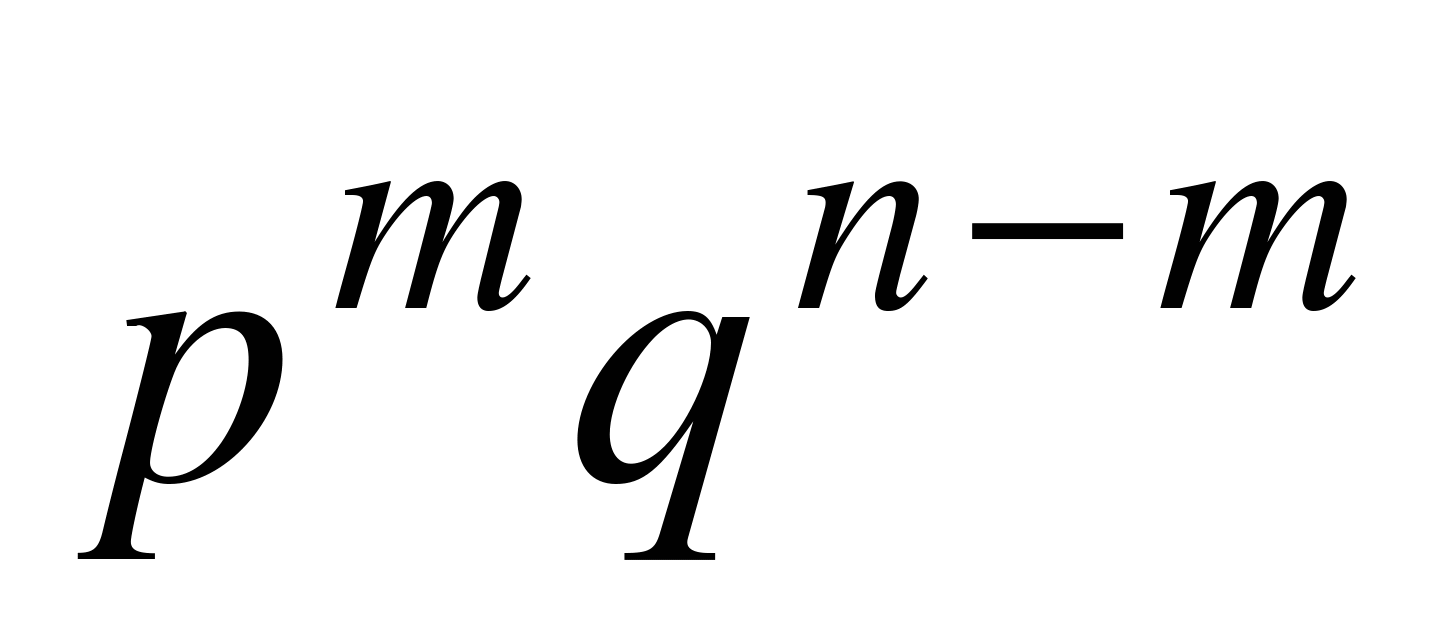

Согласно теореме сложения вероятностей, искомая вероятность 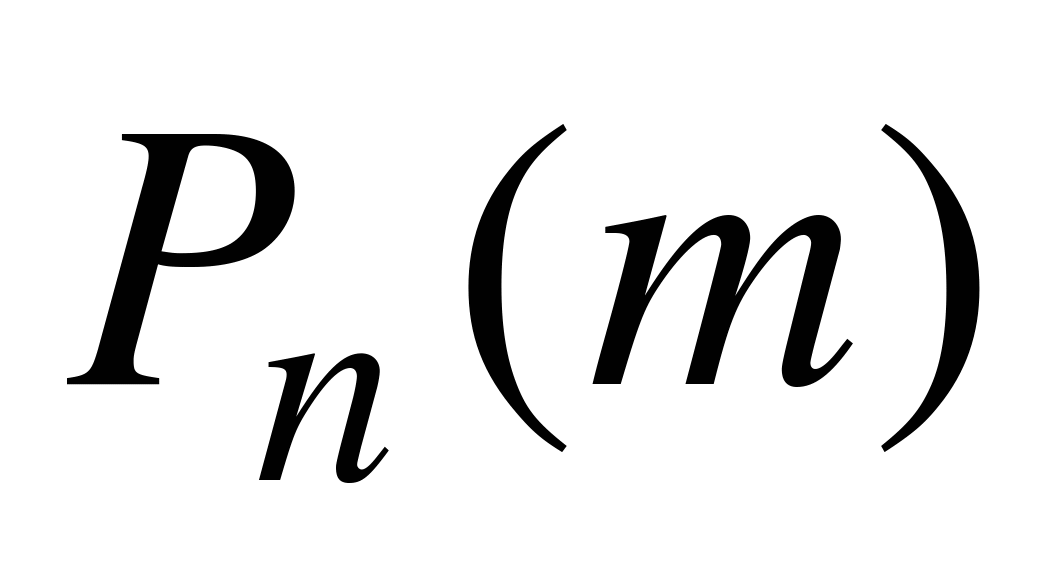равна сумме только что вычисленных вероятностей для всех различных способов выбора m испытаний из n. Но число способов выбрать m испытаний из n, как известно из комбинаторики, равно 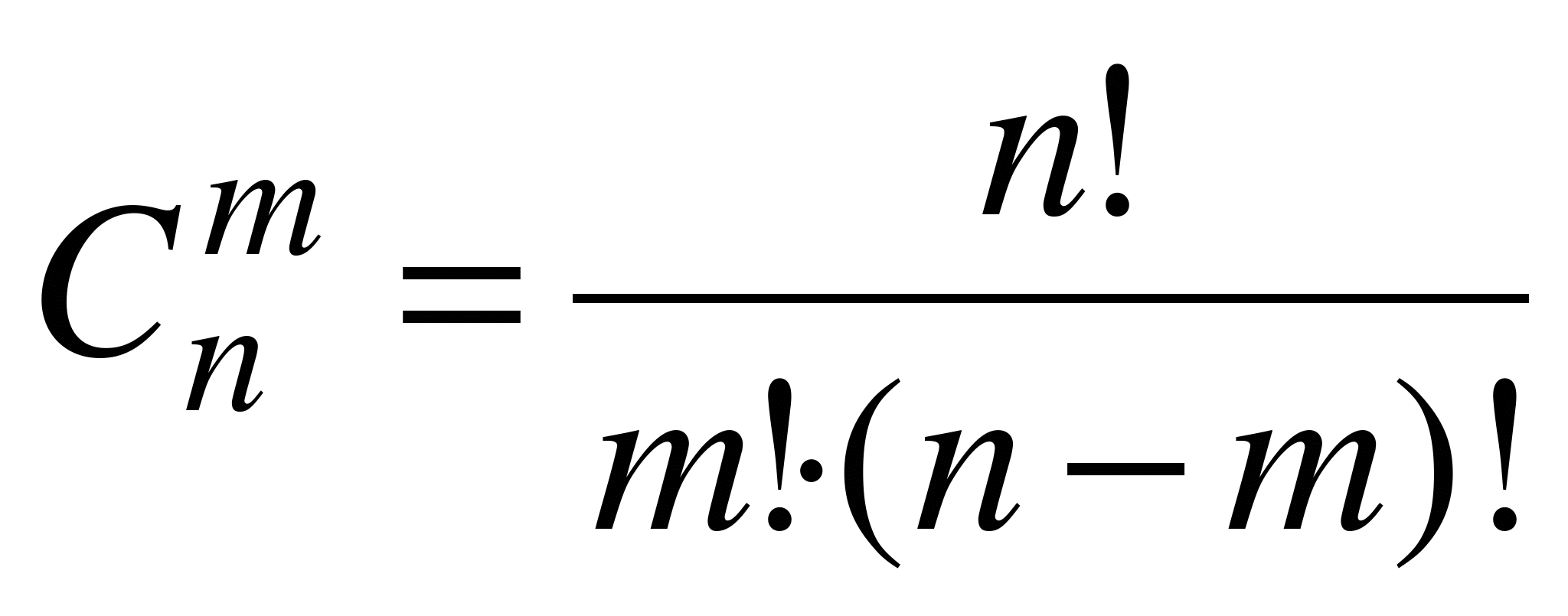. Следовательно,

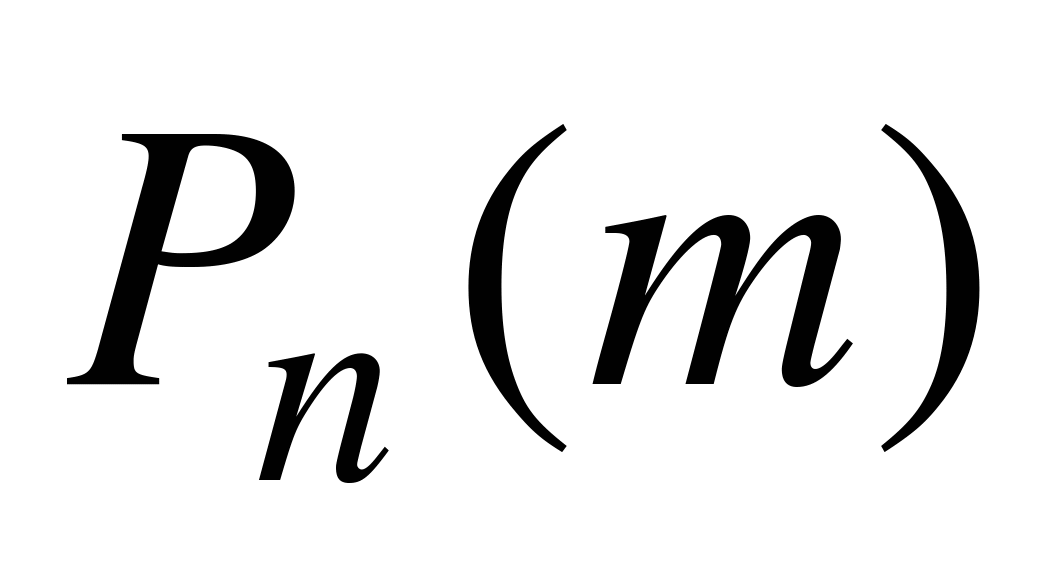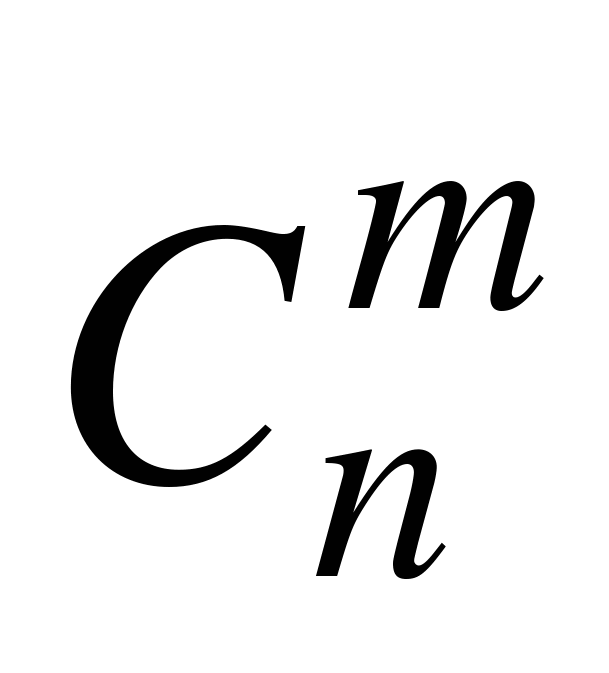
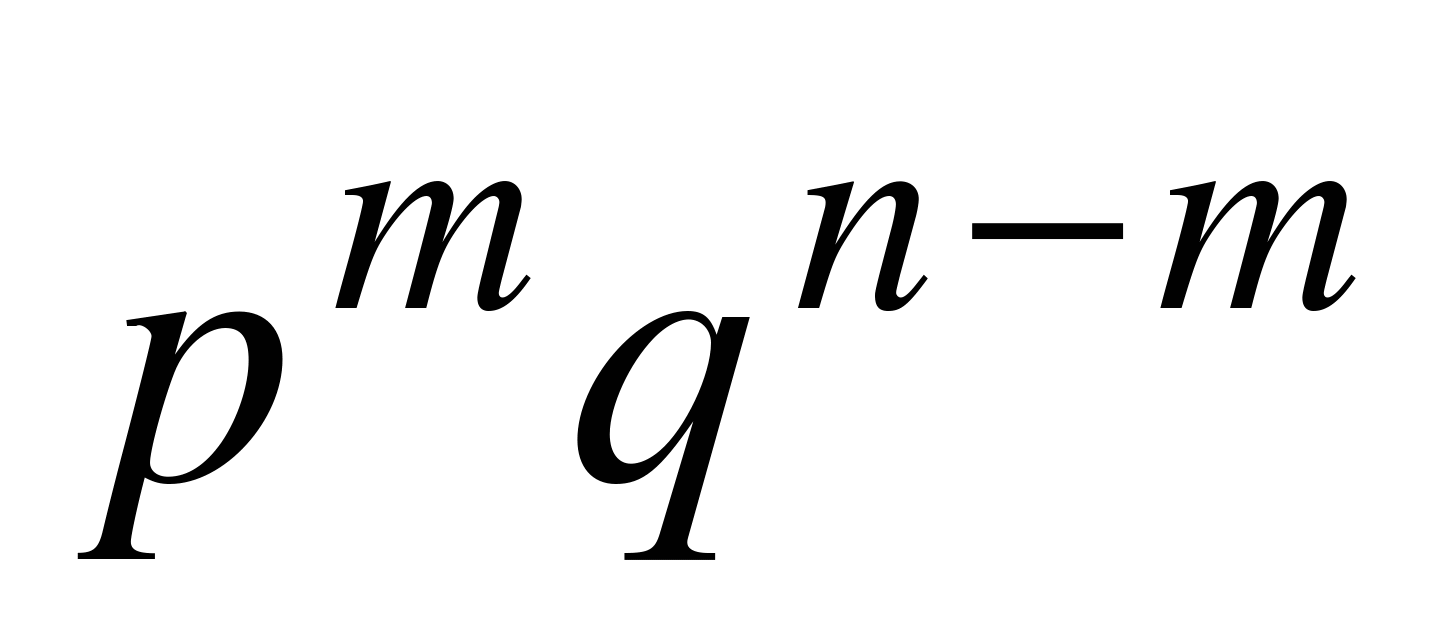= . (6.1)

Пример 6.1. Подбрасываем монету 10 раз. Найдем вероятность двукратного появления герба.

В нашем случае 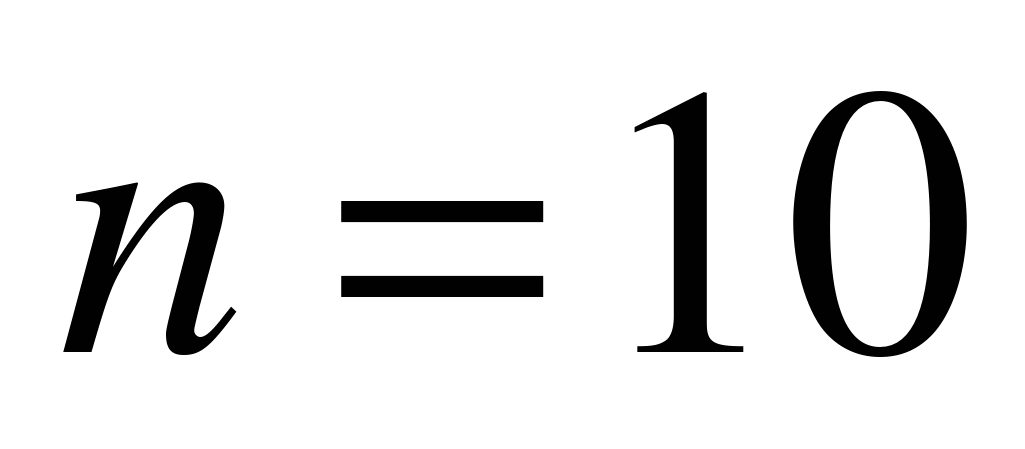, , 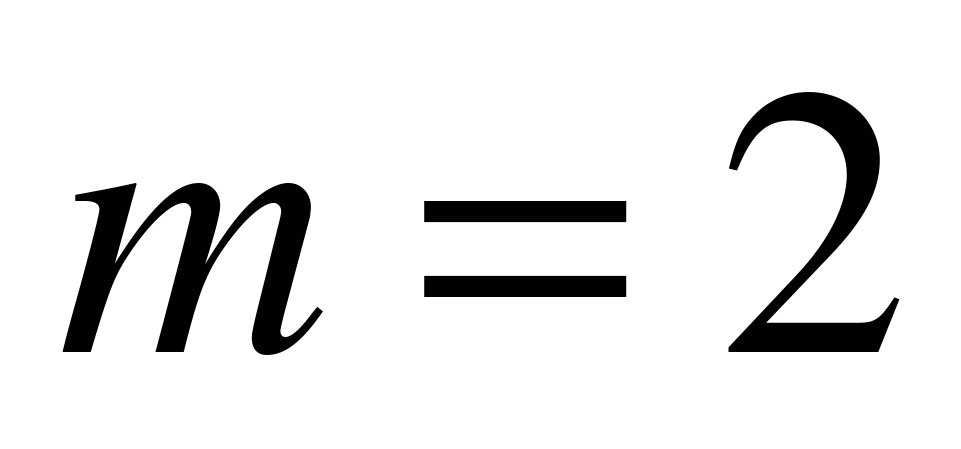, 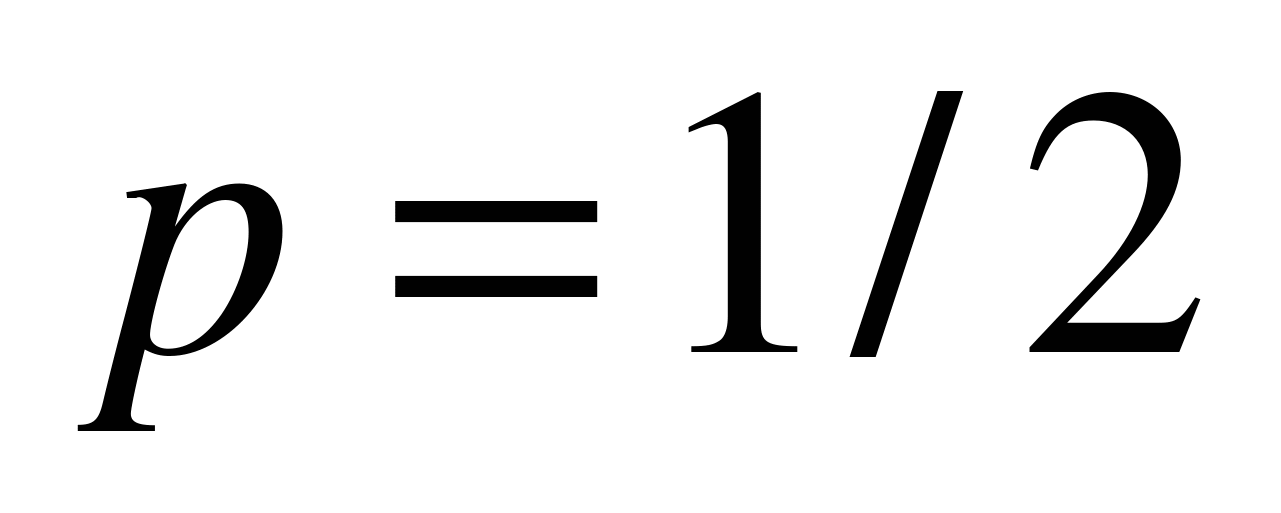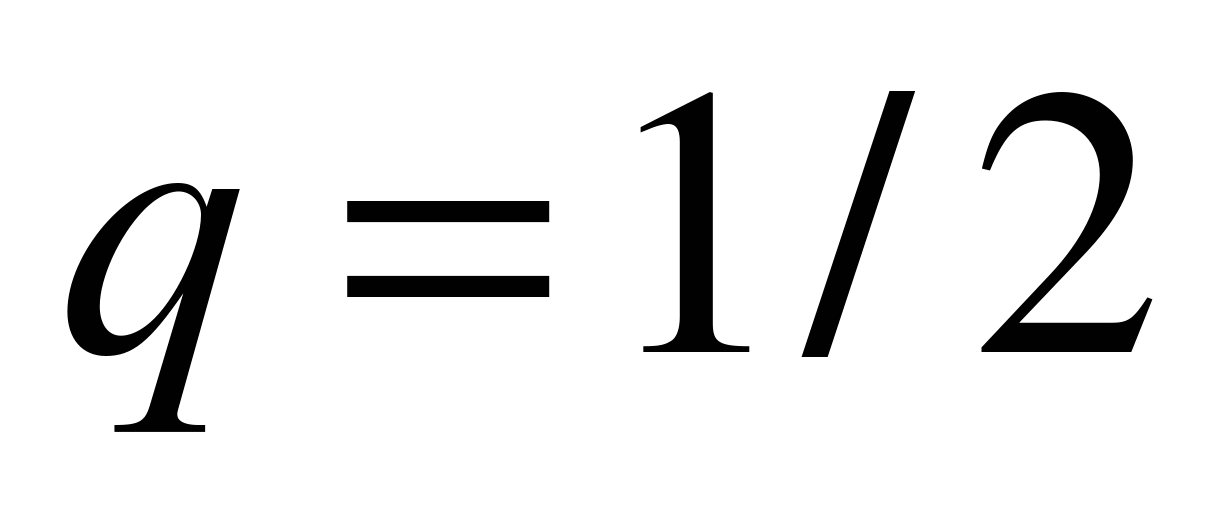. Согласно формуле (6.1) .

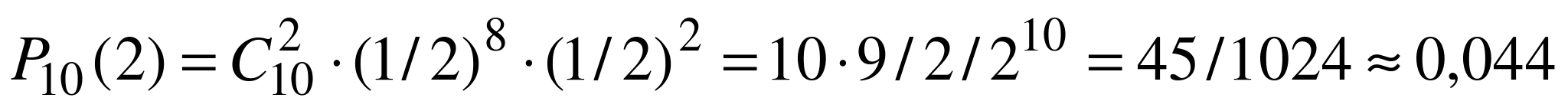Из формулы (6.1) легко заметить, что 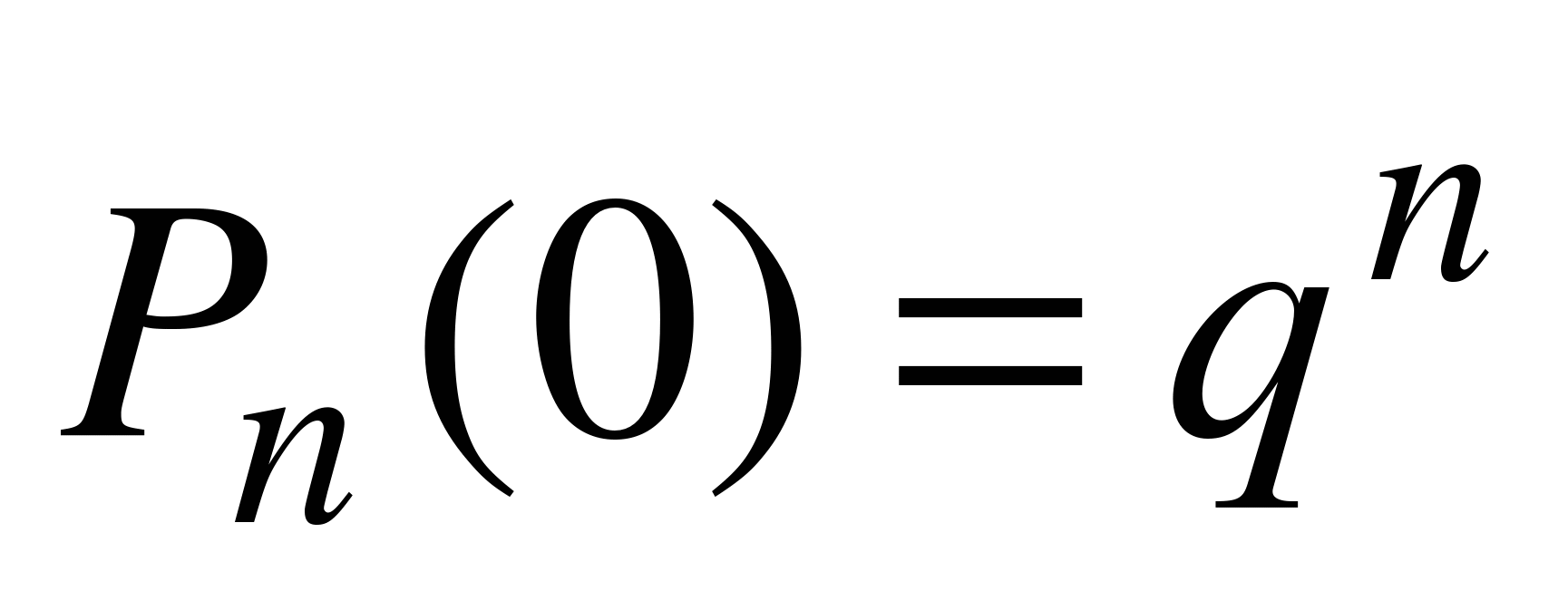, 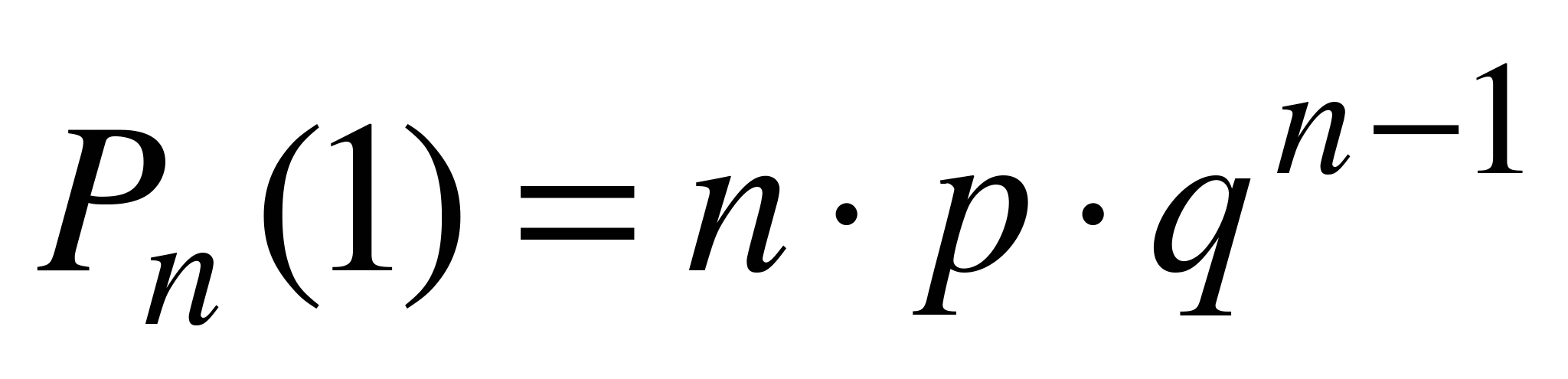и т.д. Кроме того, вероятность появления события А в n испытаниях хотя бы один раз равна

.

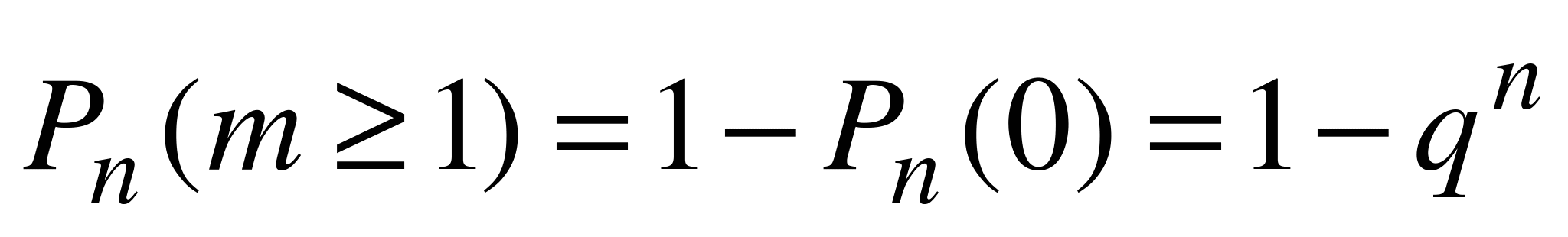Вероятность того, что событие А при проведении независимых испытаний в условиях схемы Бернулли наступит не менее k₁ раз и не более k₂ раз, обозначается 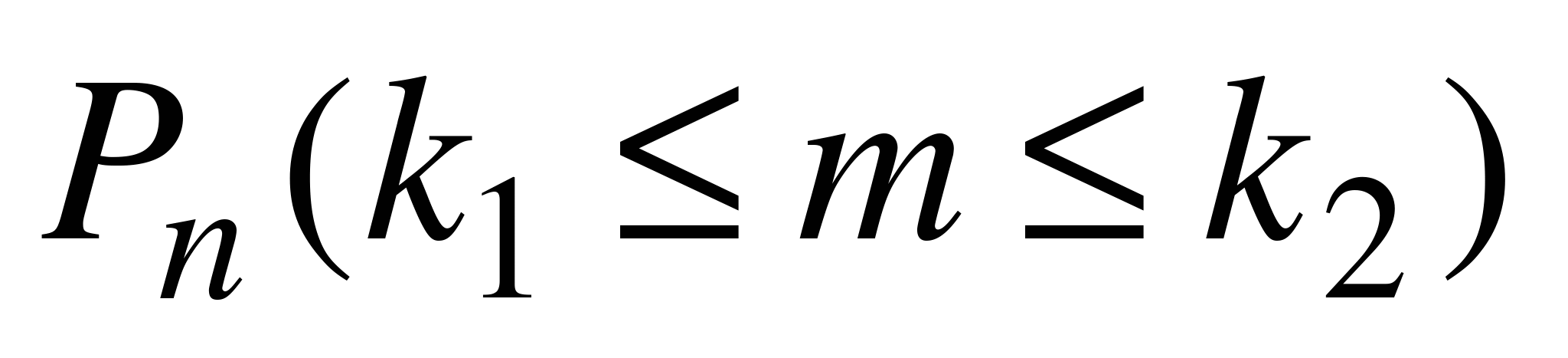и вычисляется по формуле

.

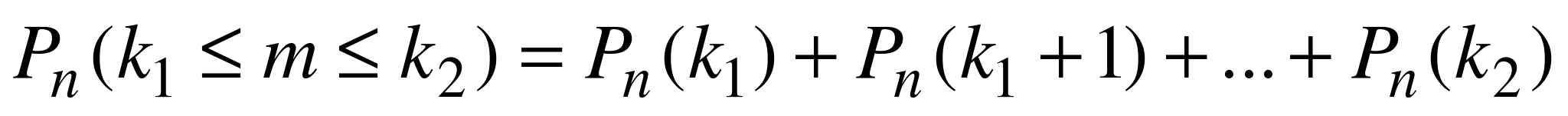Пример 6.2. Вероятность попадания стрелка в цель при одном выстреле равна 0,8. Допустим, что он стреляет по цели 6 раз. Найдем вероятность того, что стрелок попал в цель не менее четырех раз.

По условию задачи 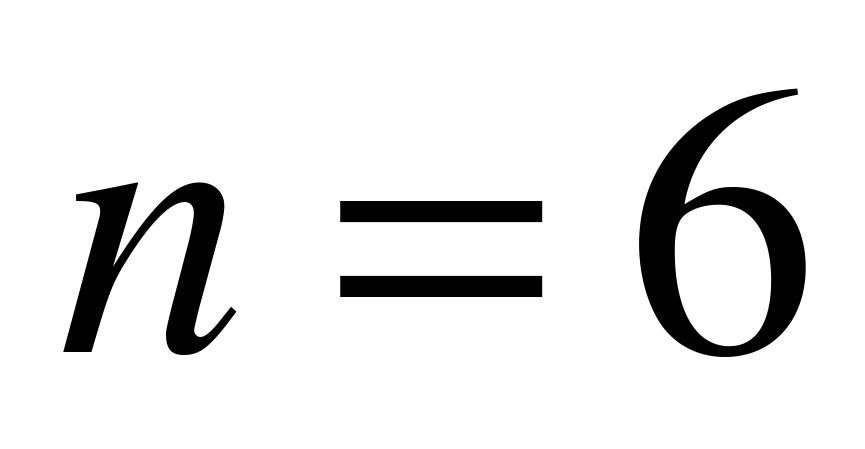, , 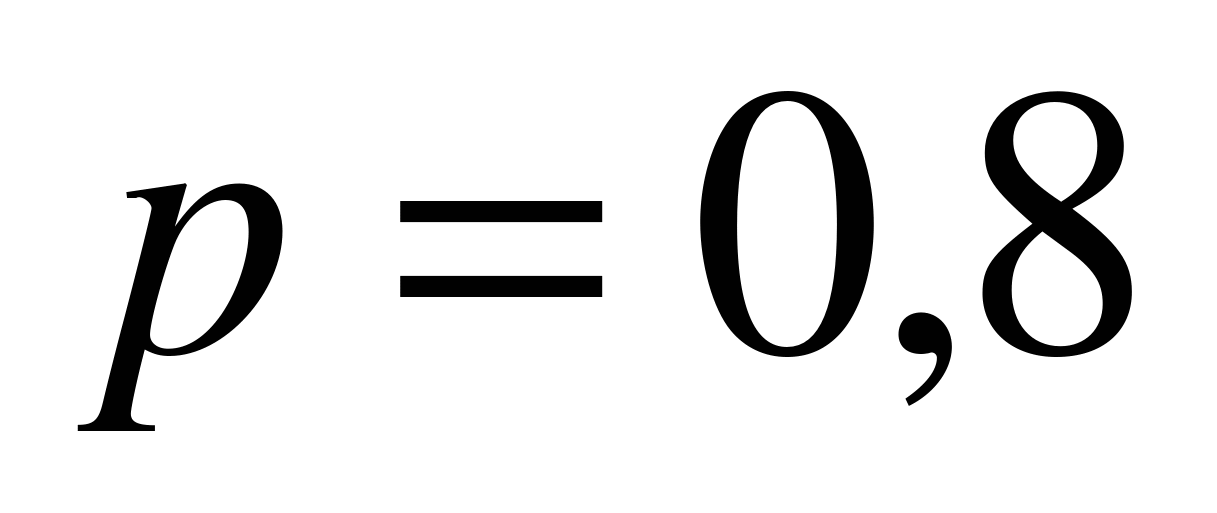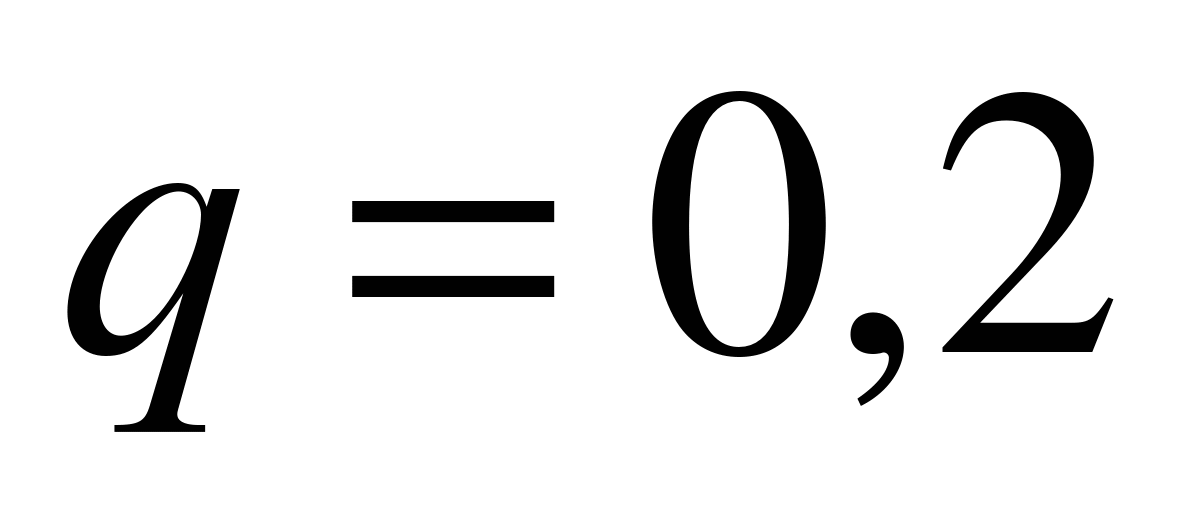. Искомая вероятность равна 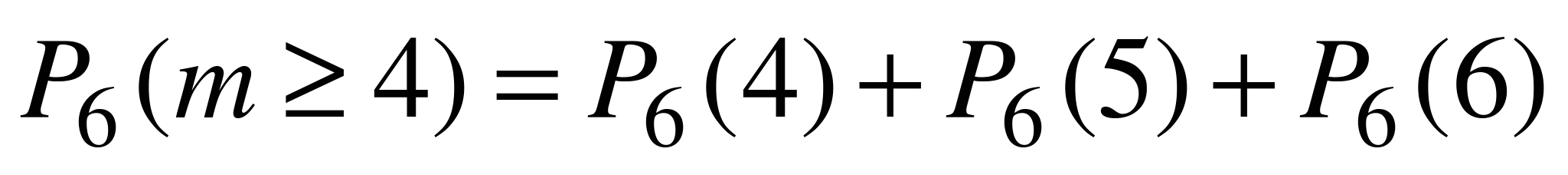. Применяя три раза формулу (6.1), находим 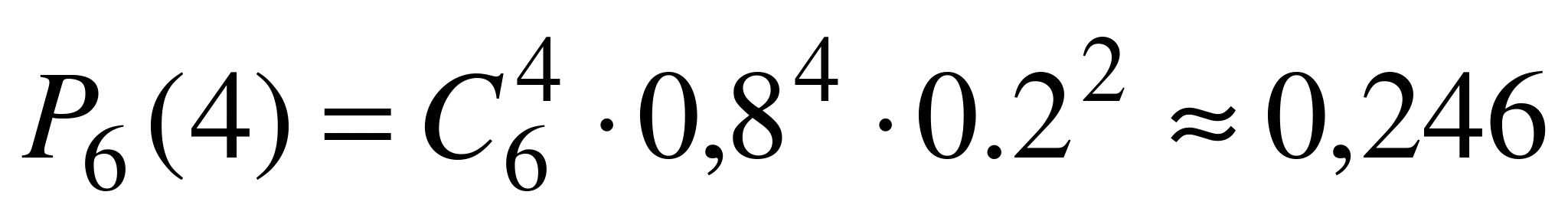, , 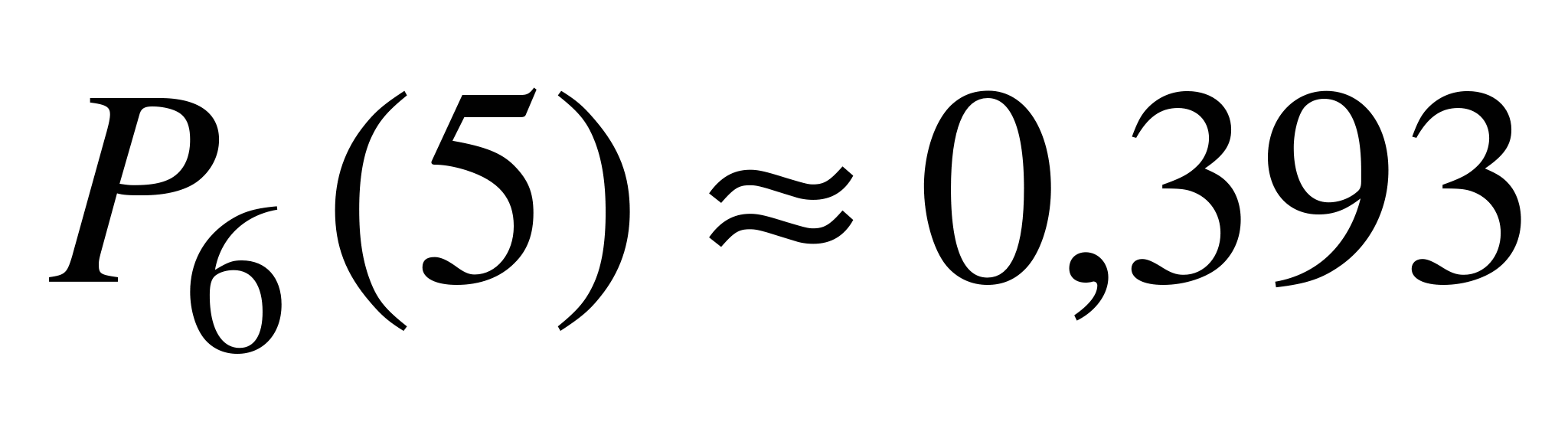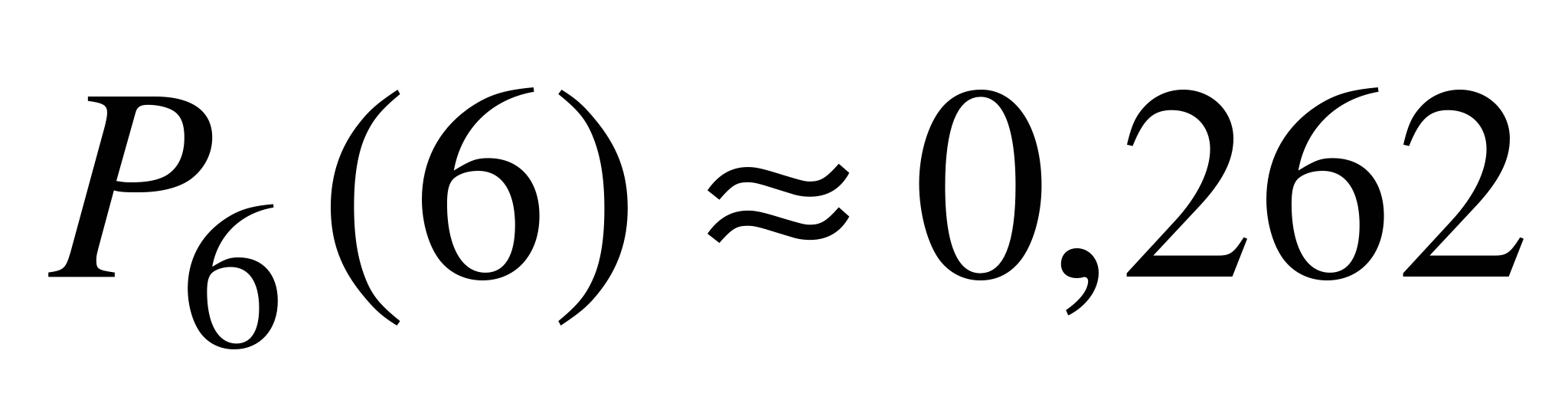. Поэтому .

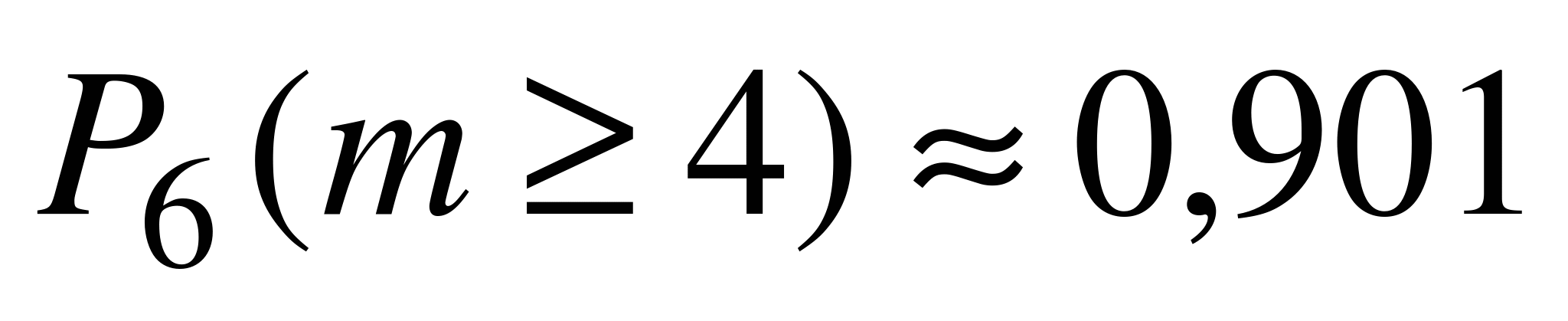Поскольку в n испытаниях событие А может произойти 0 раз или 1 раз или 2 раза … или n раз, причем перечисленные случаи включают в себя все возможности и несовместны между собой, то очевидно, что

.

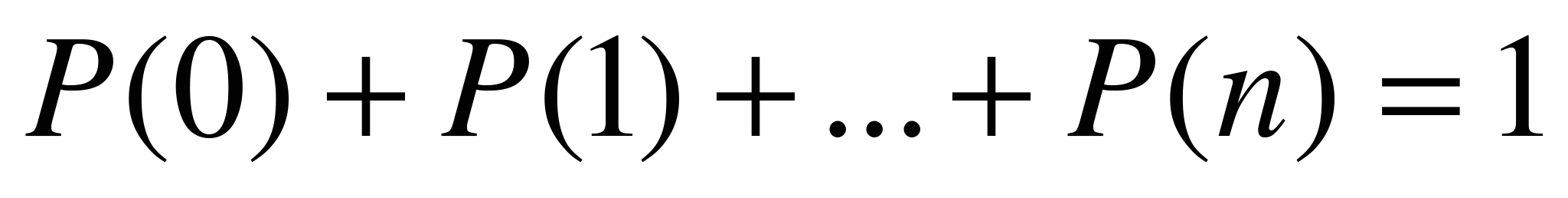Последнее соотношение может быть также получено с использованием формулы бинома Ньютона. Легко заметить, что вероятность 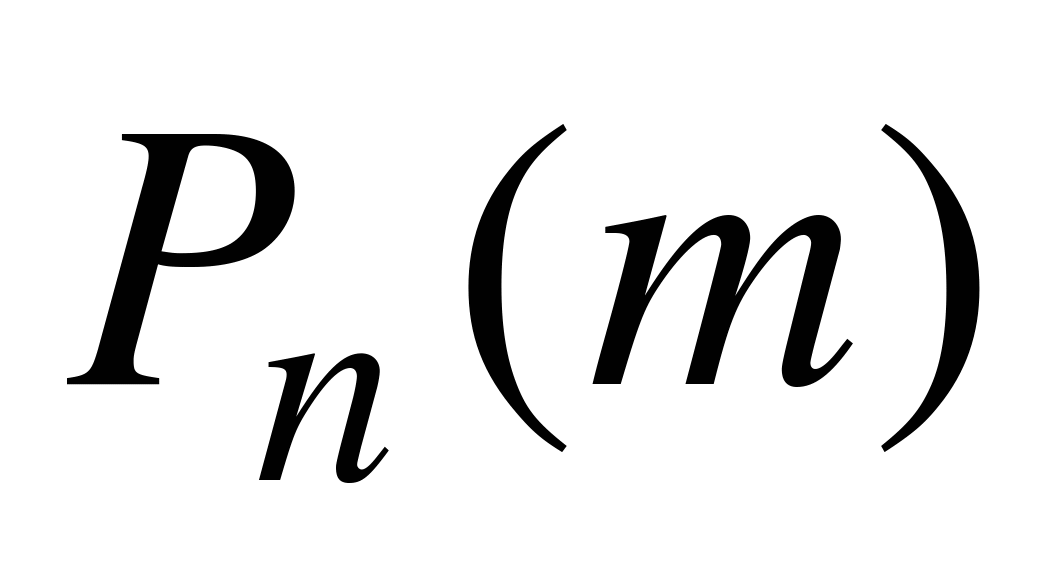равна коэффициенту при x^m в разложении бинома 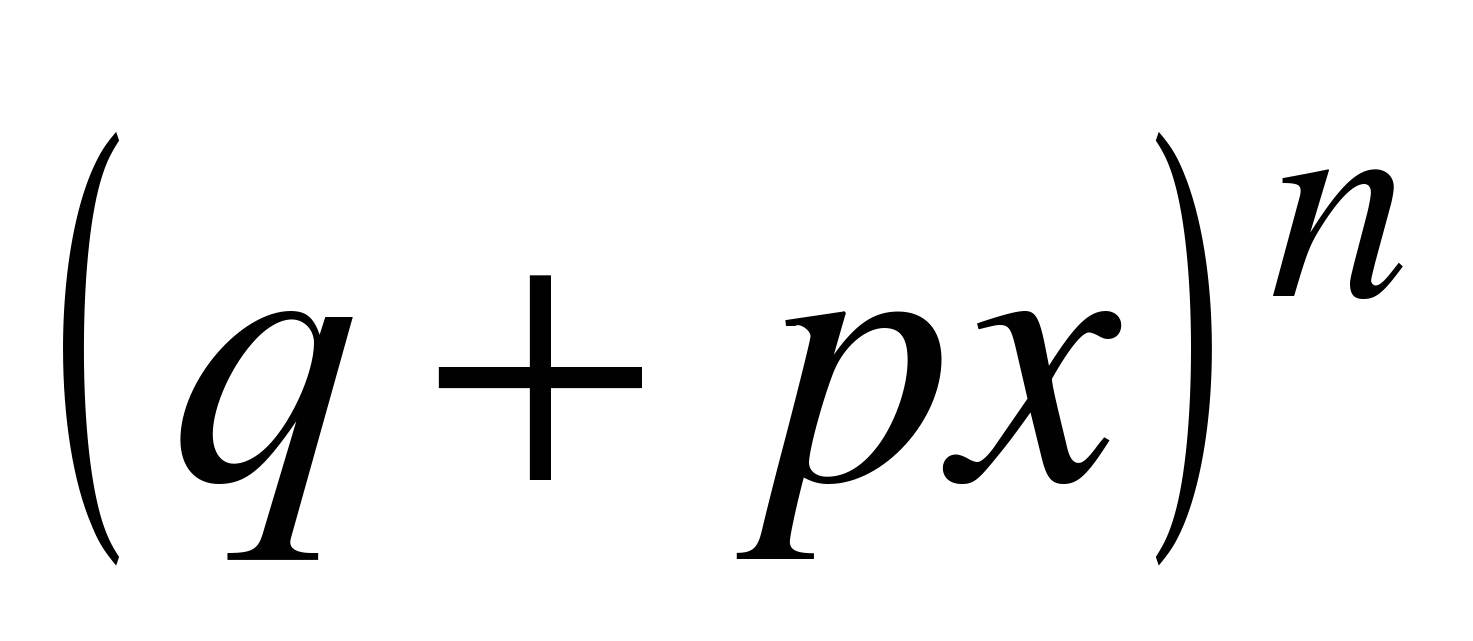по степеням x. В силу этого свойства совокупность вероятностей 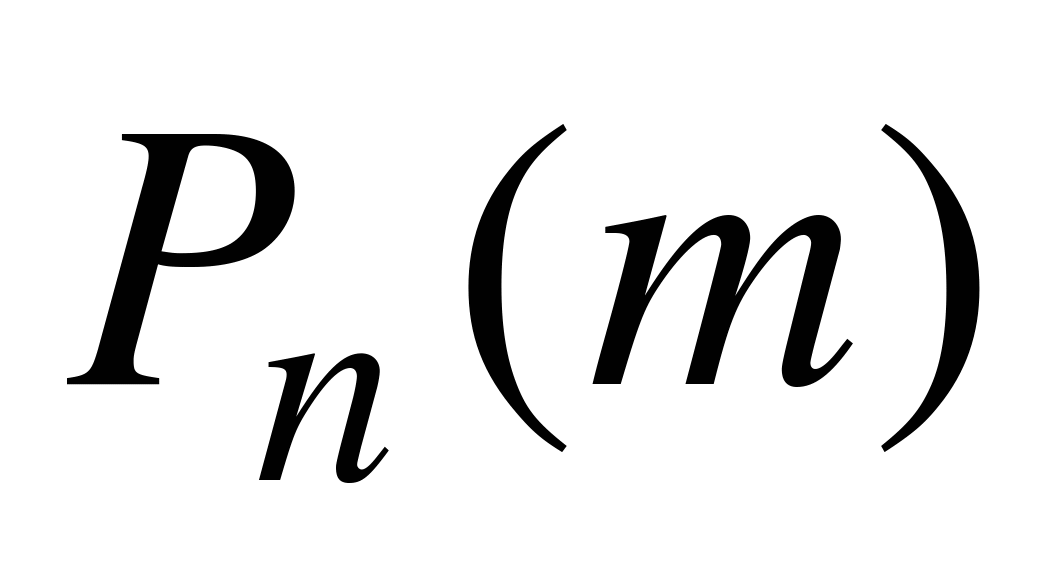называют биномиальным законом распределения вероятностей.

Отметим одно важное свойство биномиального распределения.

При фиксированном значении n вероятность 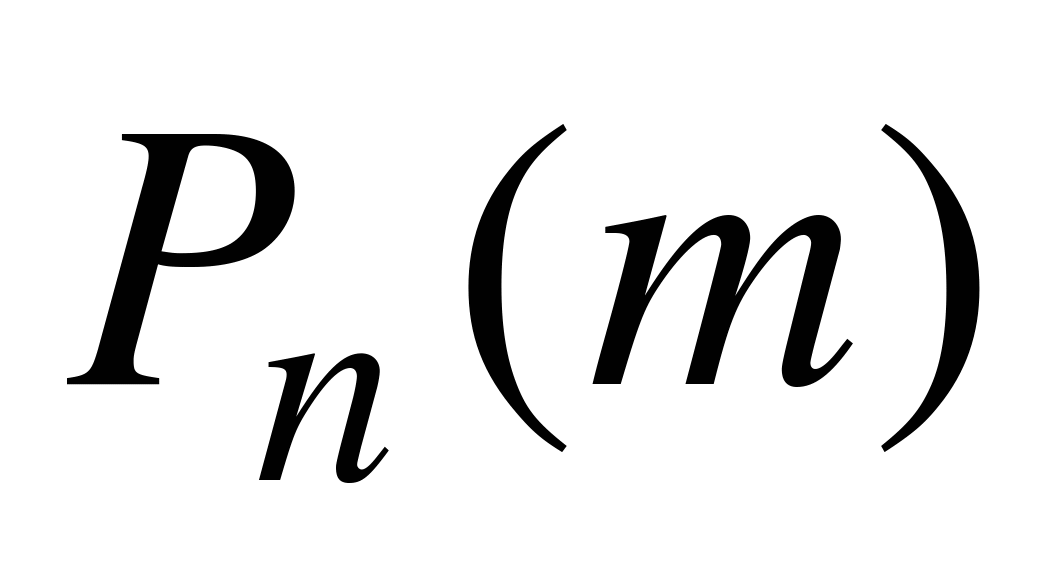с увеличением m сначала возрастает, затем достигает своего максимального значения и при дальнейшем росте m убывает.

Докажем это свойство. Из формулы (6.1) легко получить соотношение .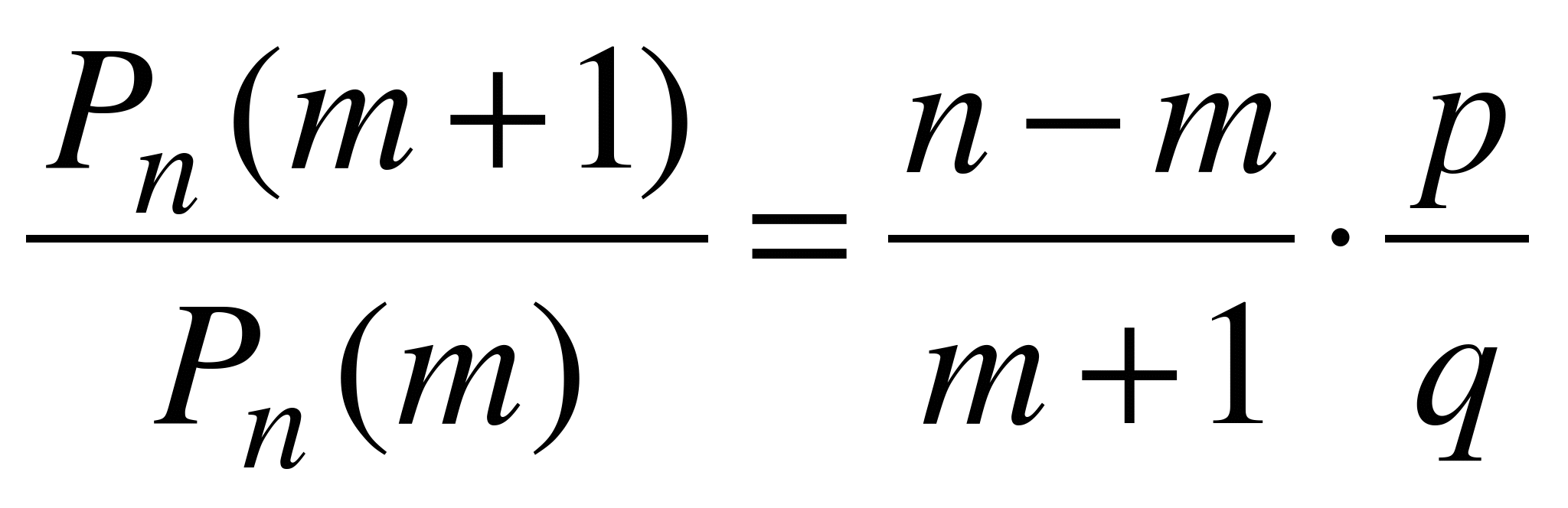

Тогда 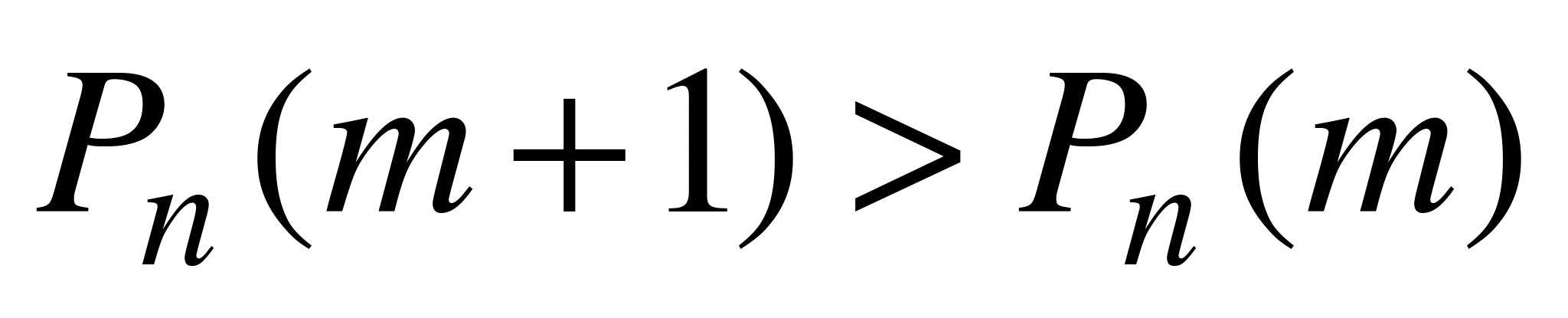, если 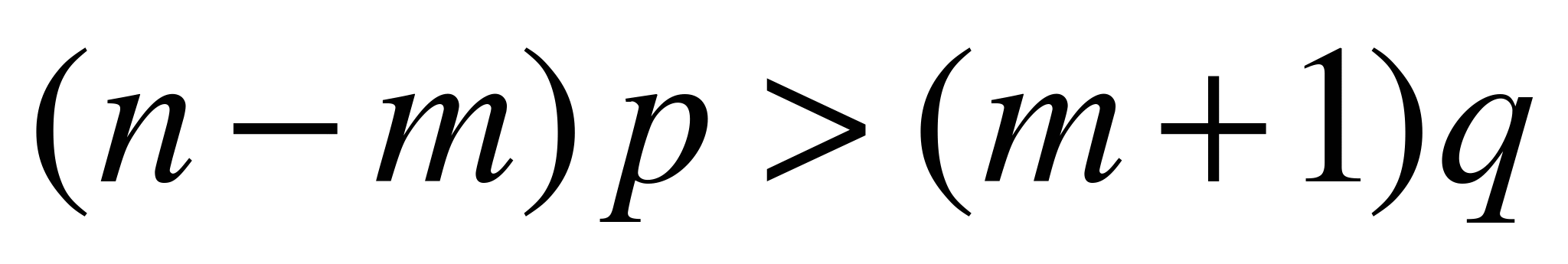, т.е. если 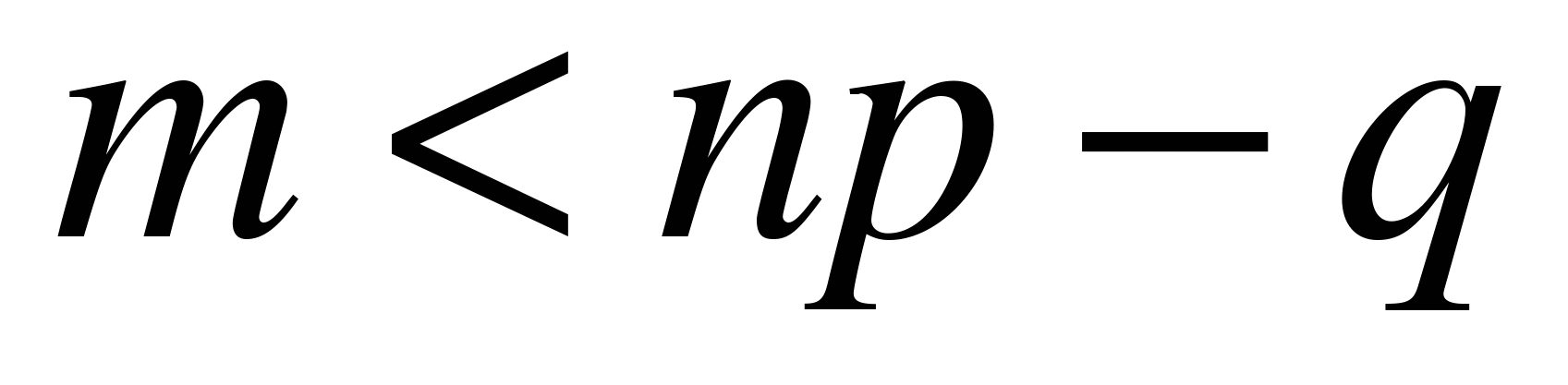. 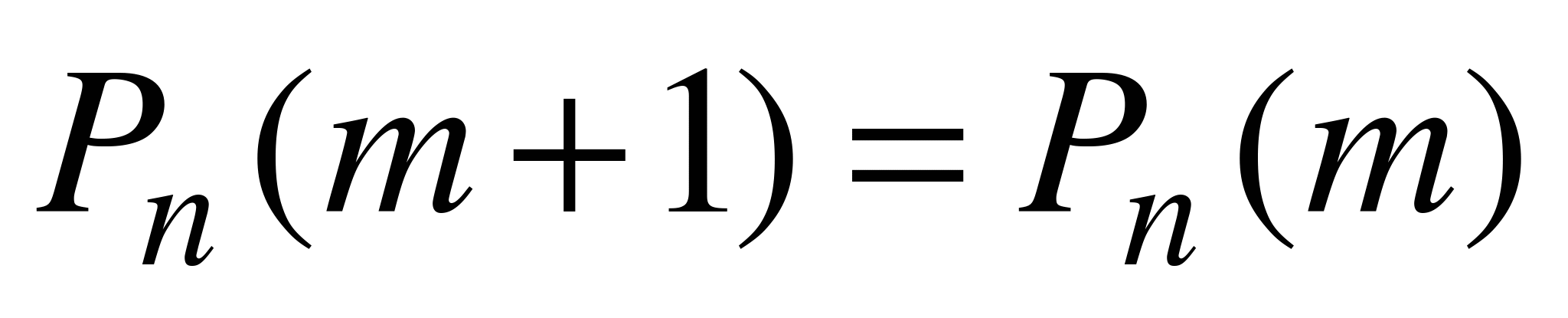, есл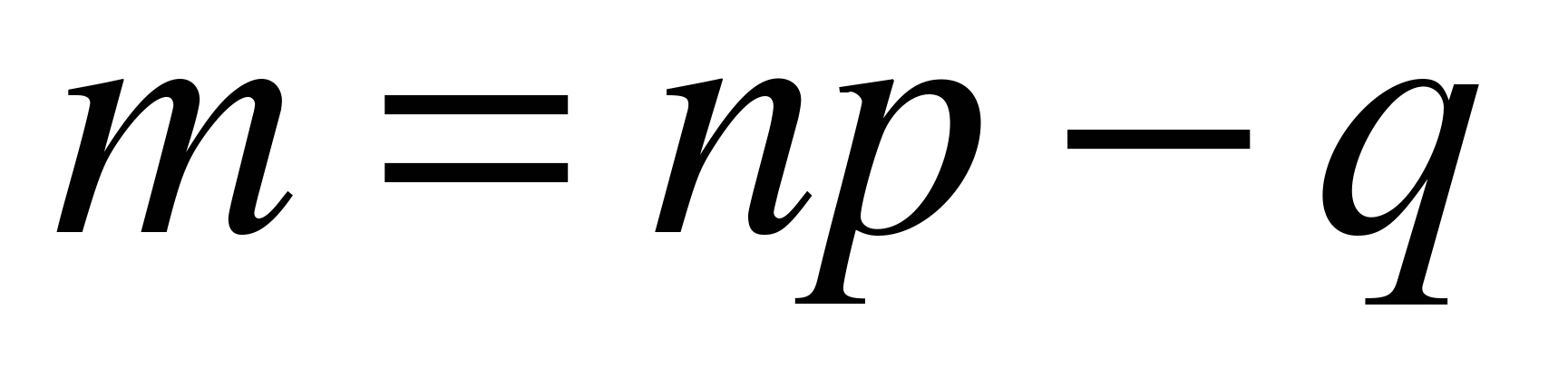и , и 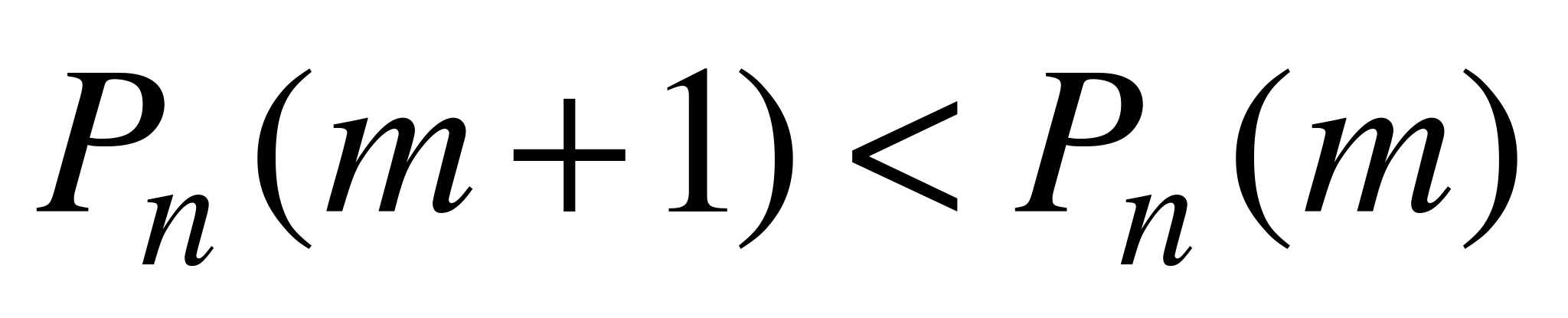, если .

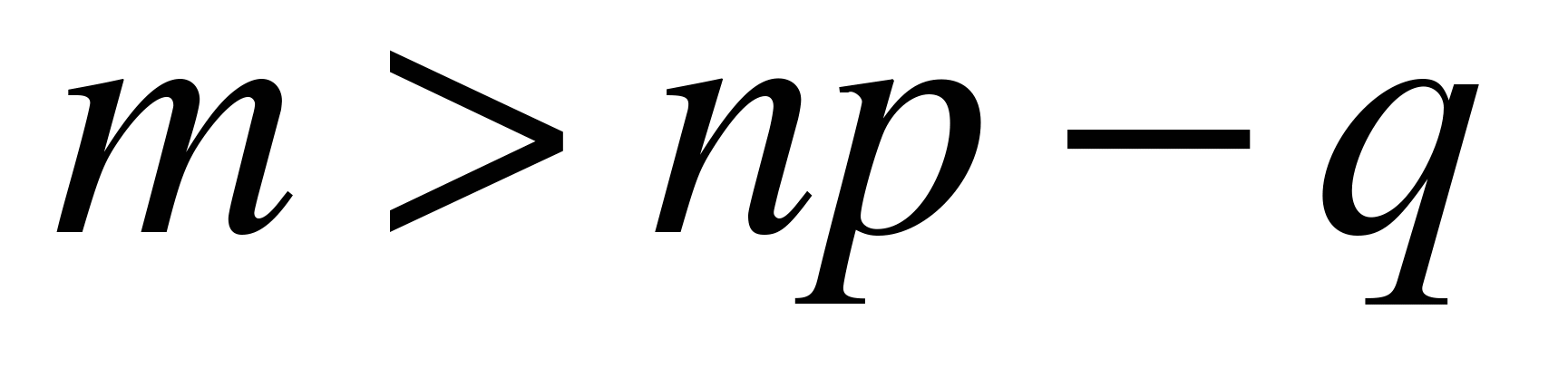Значение m₀ , при котором вероятность 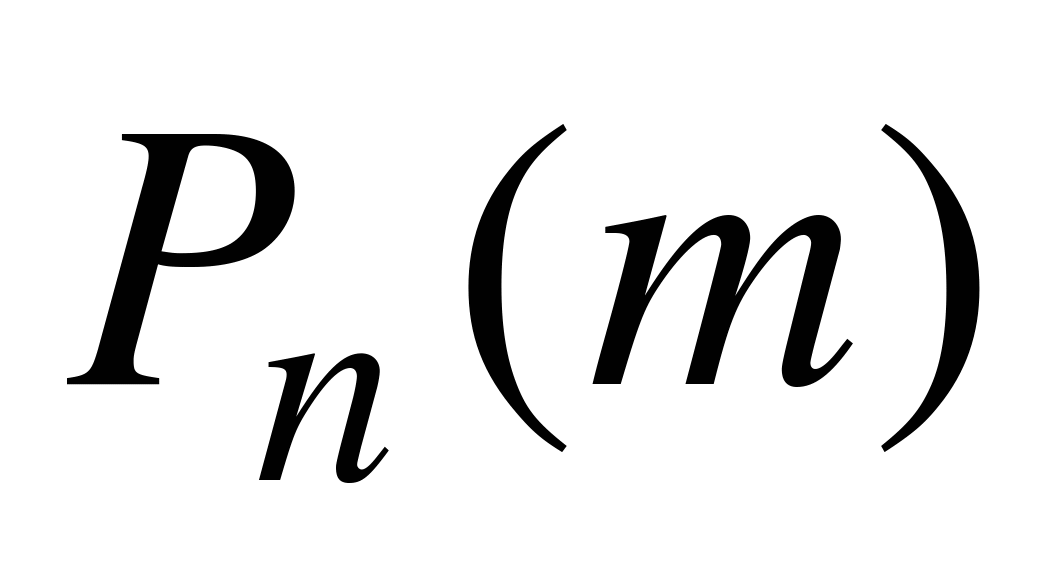принимает наибольшее значение, называется вероятнейшим (или наиболее вероятным) значением. Как следует из предыдущих оценок, вероятнейшее значение удовлетворяет неравенству

.

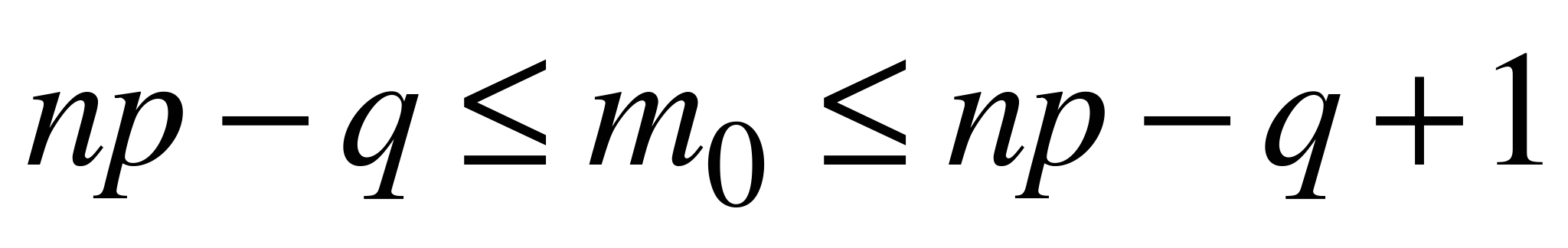Учитывая, что q = 1 - p, последнее неравенство можно переписать в виде

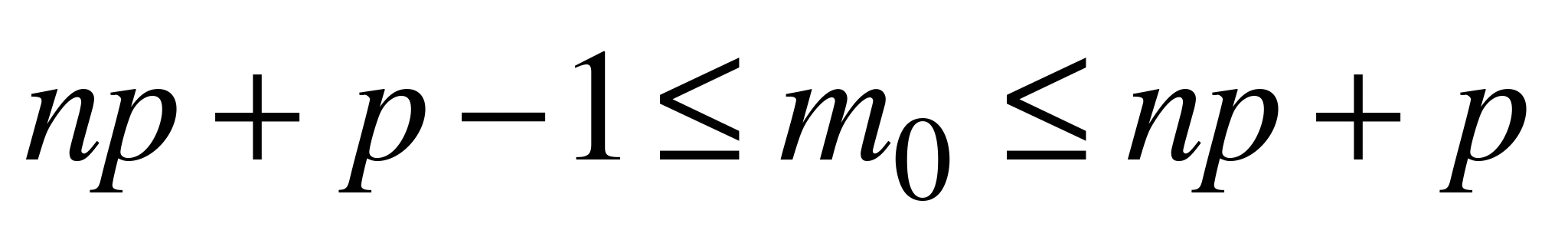. (6.2)

Если 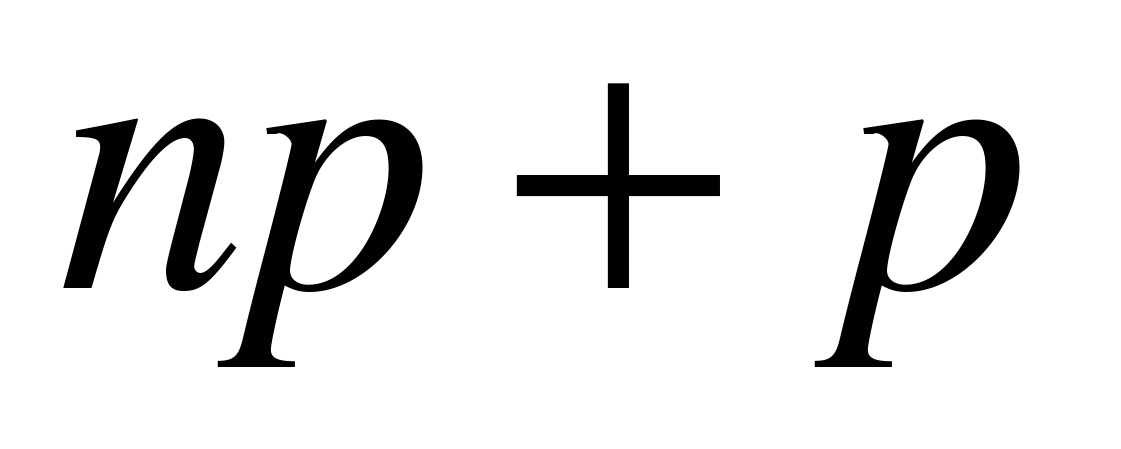является целым числом, то наиболее вероятных значений два: 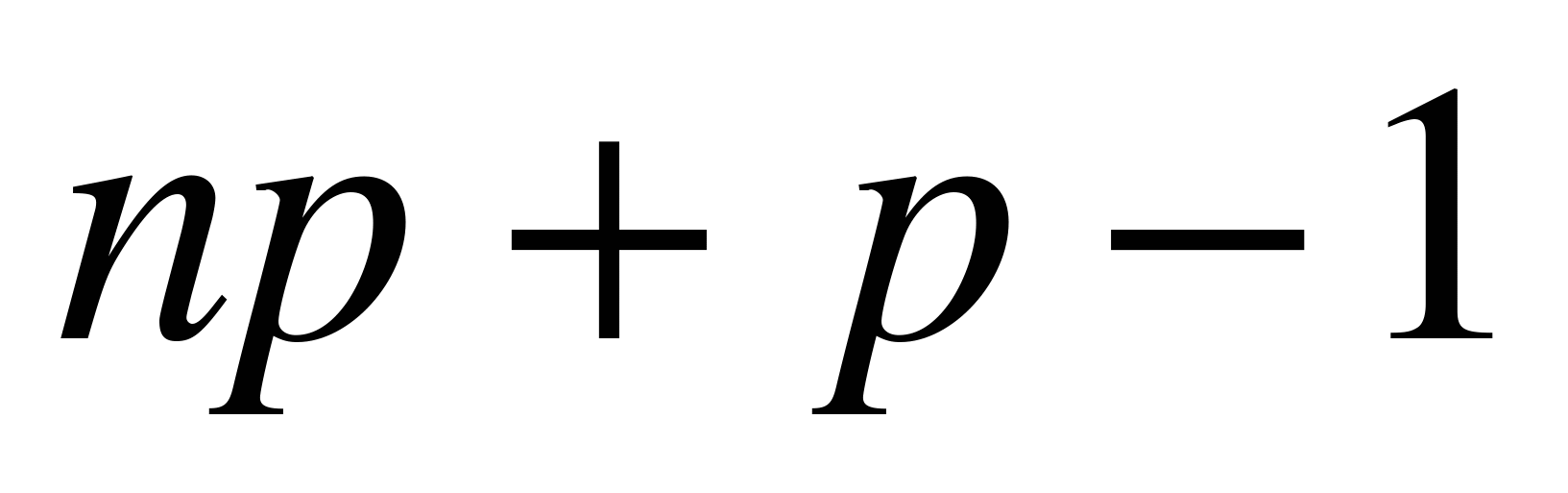и .

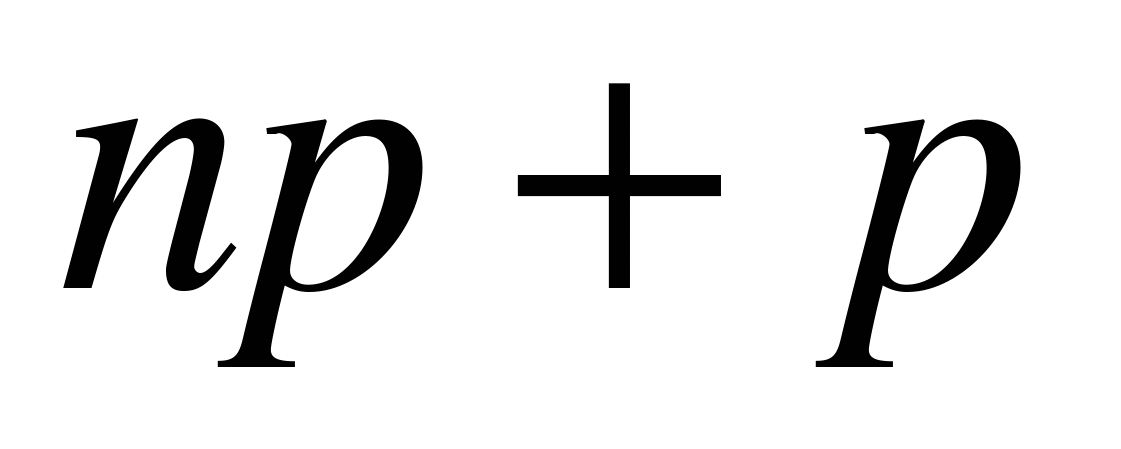Пример 6.3. В условиях примера 6.2 найдем вероятнейшее значение числа попаданий стрелка.

В этом примере 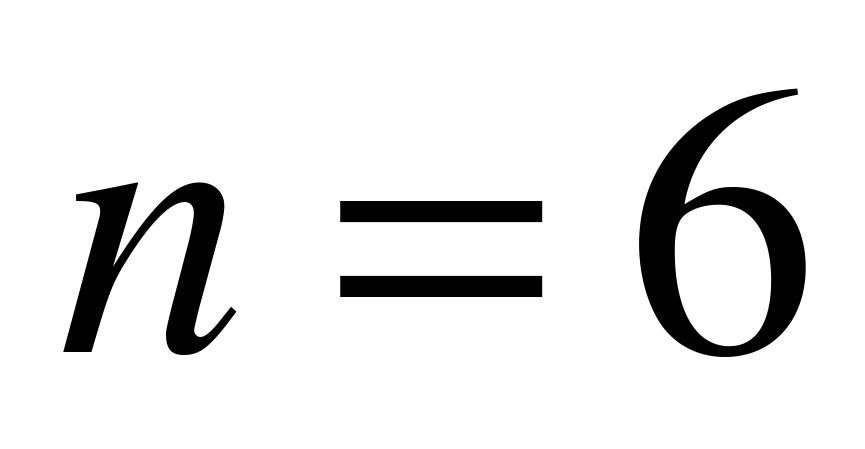, , 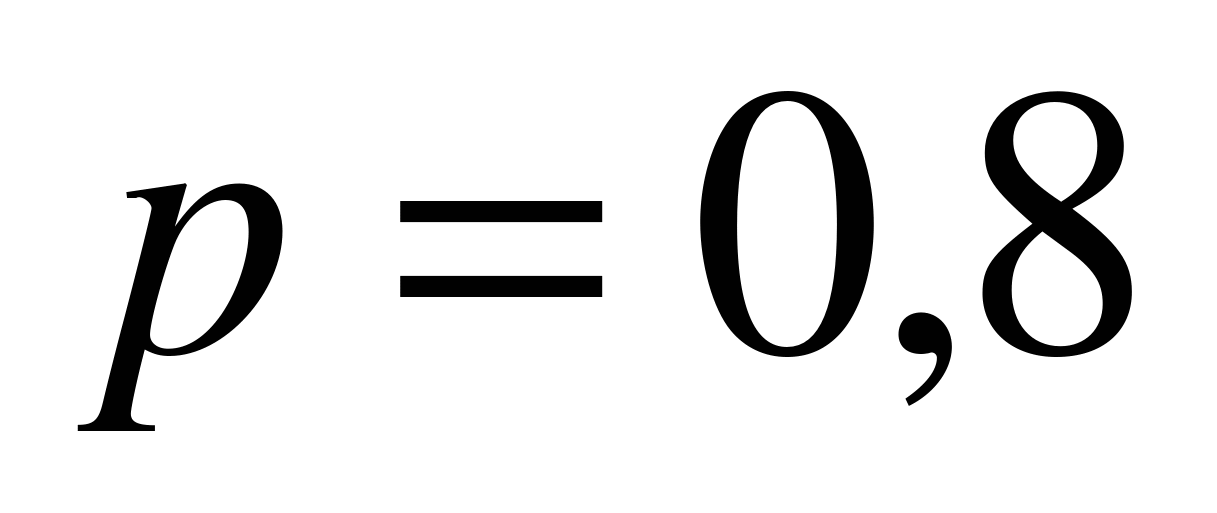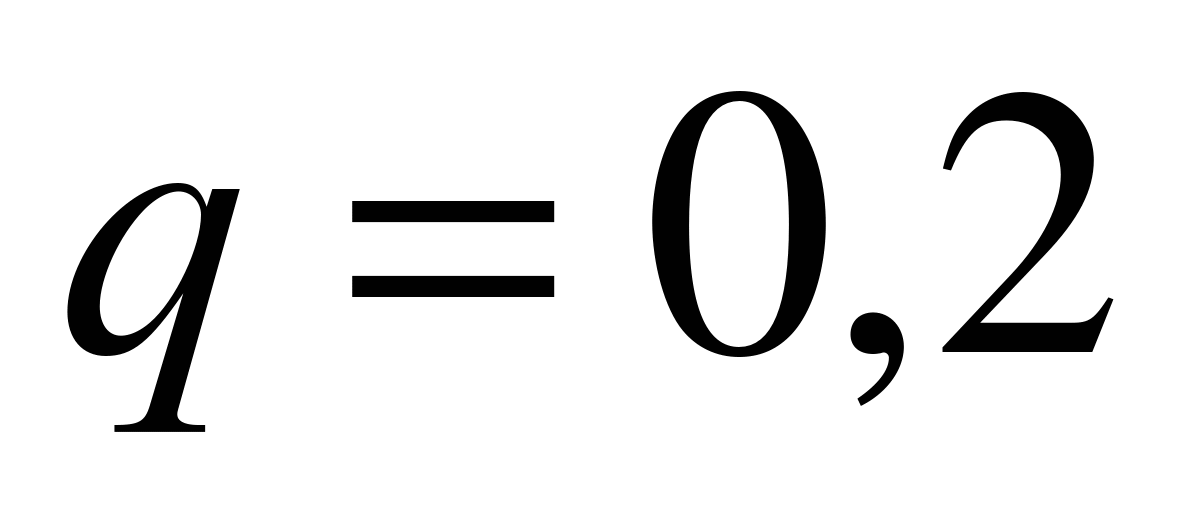. Поэтому в силу неравенства (6.2), 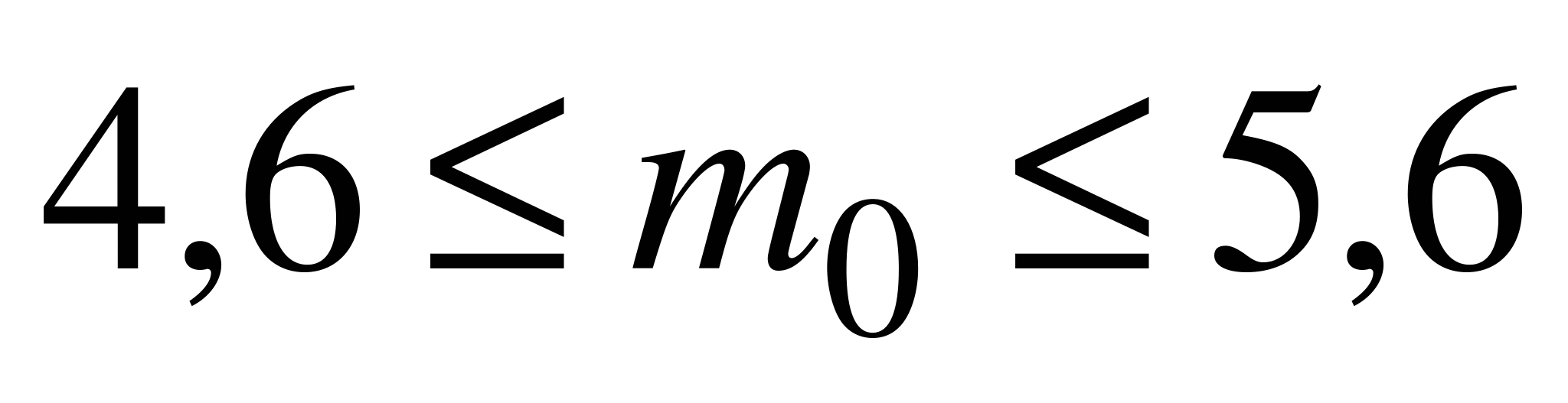. Это означает, что при данных условиях наиболее вероятное число попаданий равно пяти.

Пример 6.4. Пусть стрелок стреляет по цели 50 раз, а вероятность попадания стрелка в цель при одном выстреле равна 1/3. Вычислим наиболее вероятное число попаданий.

Применяя формулу (6.2), имеем 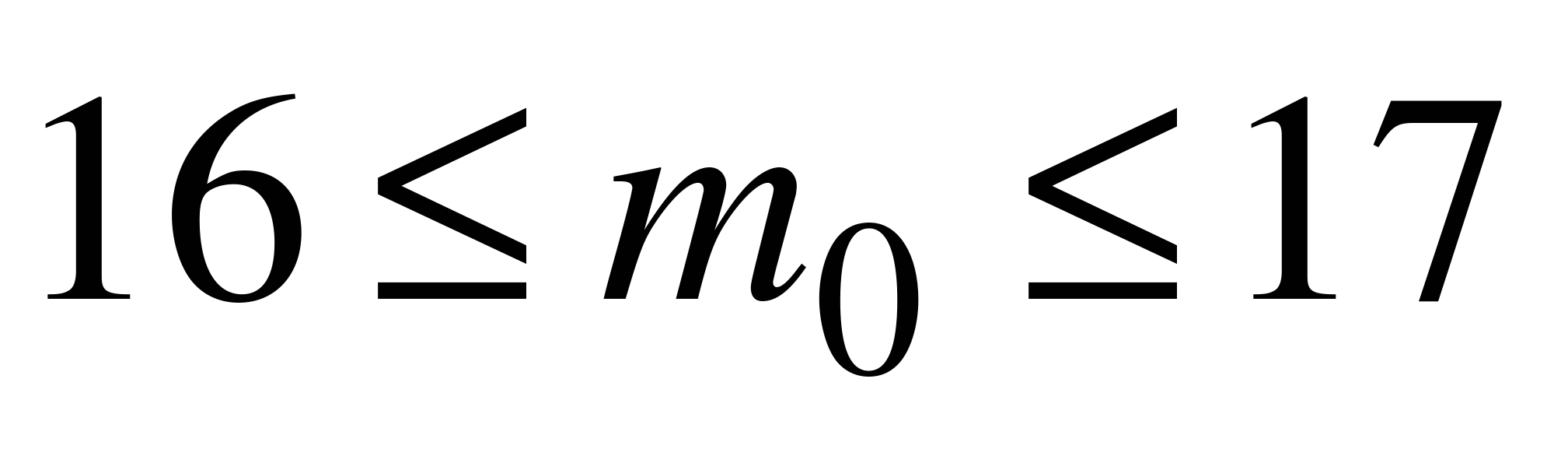. Значит, вероятнейших значений два. Вероятнее всего, что в данных условиях стрелок попадет в цель 16 или 17 раз.

В условиях схемы Бернулли вычисления вероятности по формуле (6.1) удобны только при достаточно маленьких значениях m и n. При больших значениях m и n вычисление 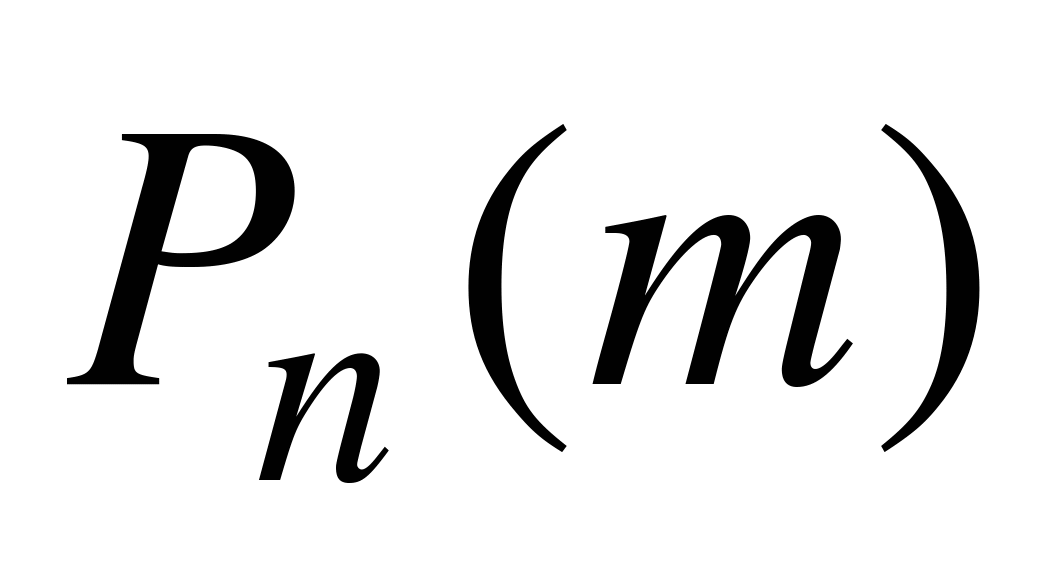представляет значительные трудности, главным образом, из-за сложности подсчета факториалов в формуле числа сочетаний. Поэтому возникает необходимость в приближенных формулах, позволяющих с достаточной степенью точности определять эти вероятности. Впервые формула такого рода была найдена Муавром в 1730 году для частного случая схемы Бернулли при 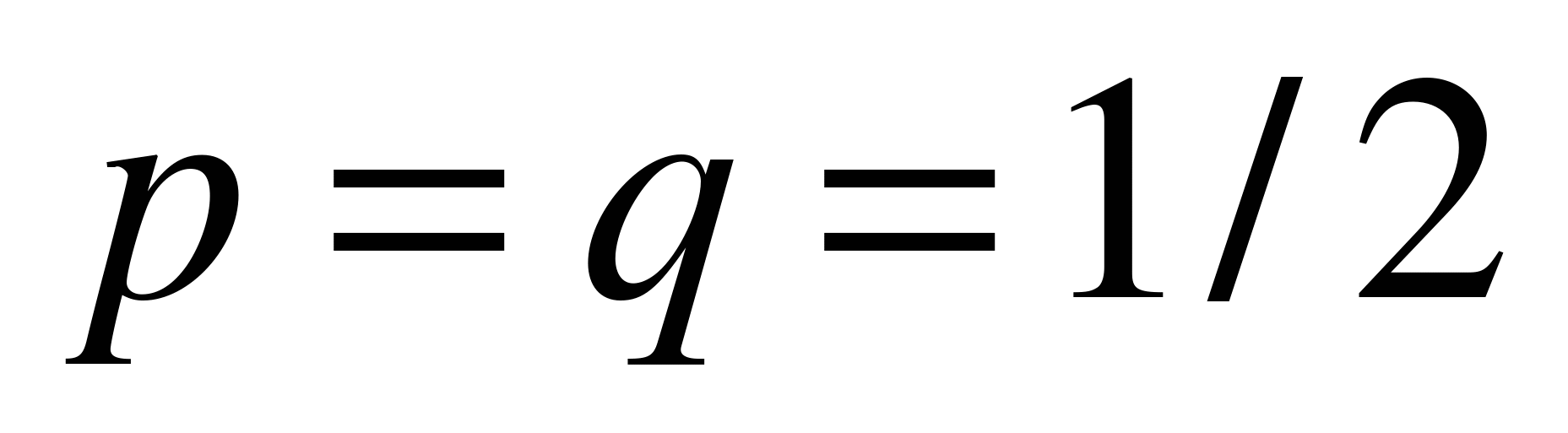, а затем обобщена Лапласом на случай произвольного p, отличного от 0 и 1. Эта формула получила название локальной теоремы Муавра - Лапласа.

Локальная теорема Муавра-Лапласа.

Вусловиях схемы Бернулли т.е. при проведении n независимых испытаний с двумя исходами, в каждом из которых вероятность появления события А постоянна и равна p (0< p <1), а вероятность появления противоположного события равна q =1 –p, для 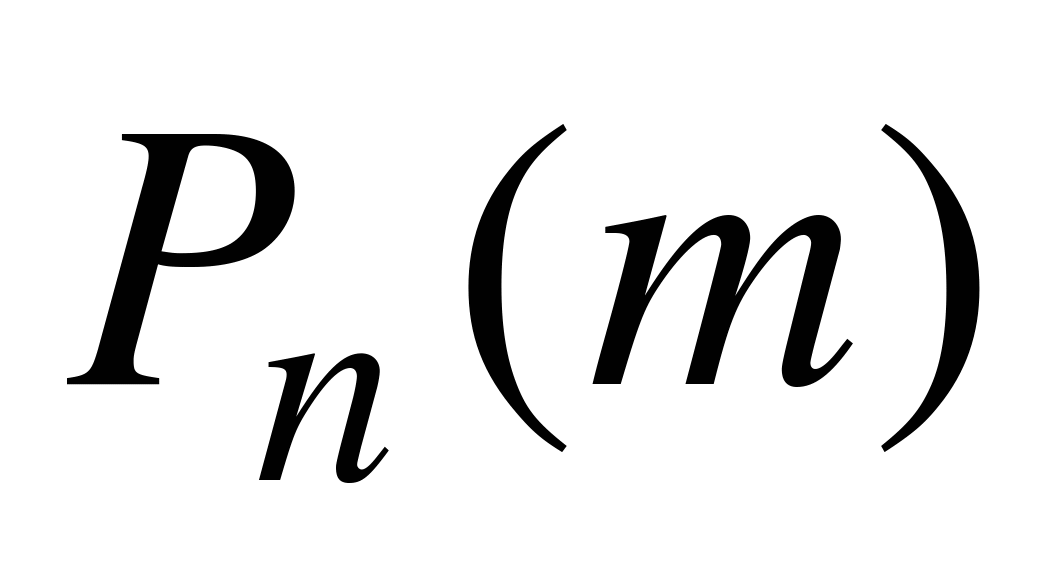(вероятности того, что в этих испытаниях событие А наступит ровно m раз) имеет место приближенное равенство

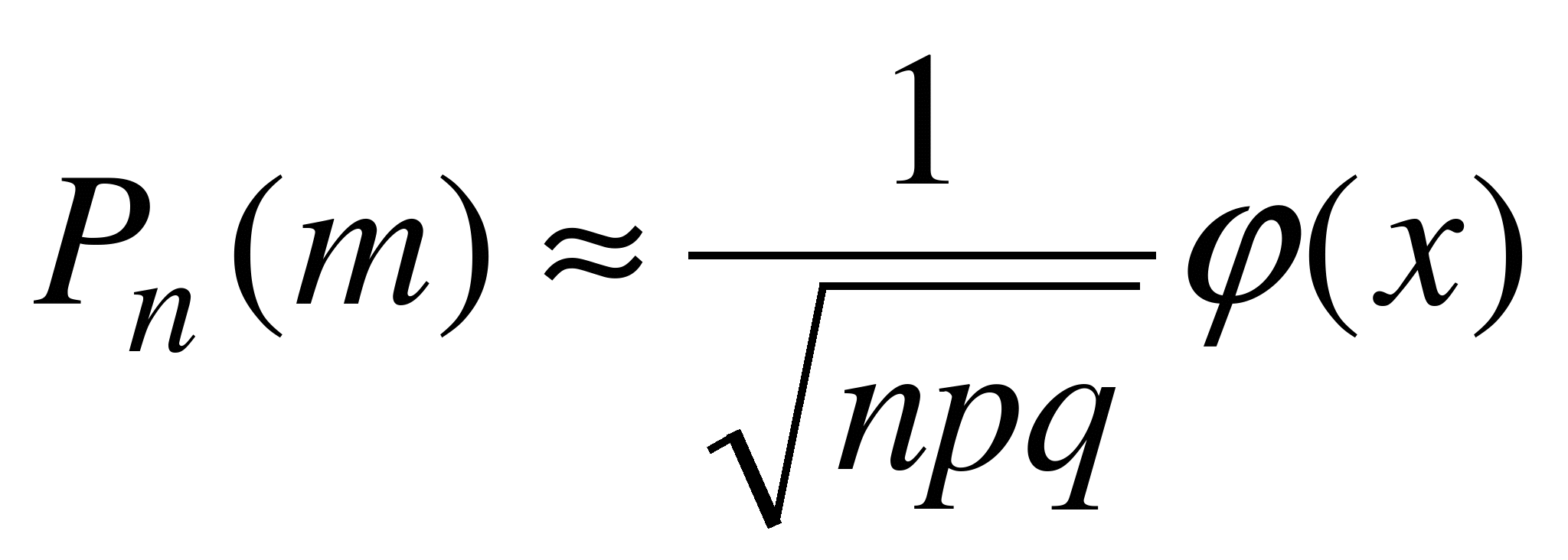, (6.3)

где , .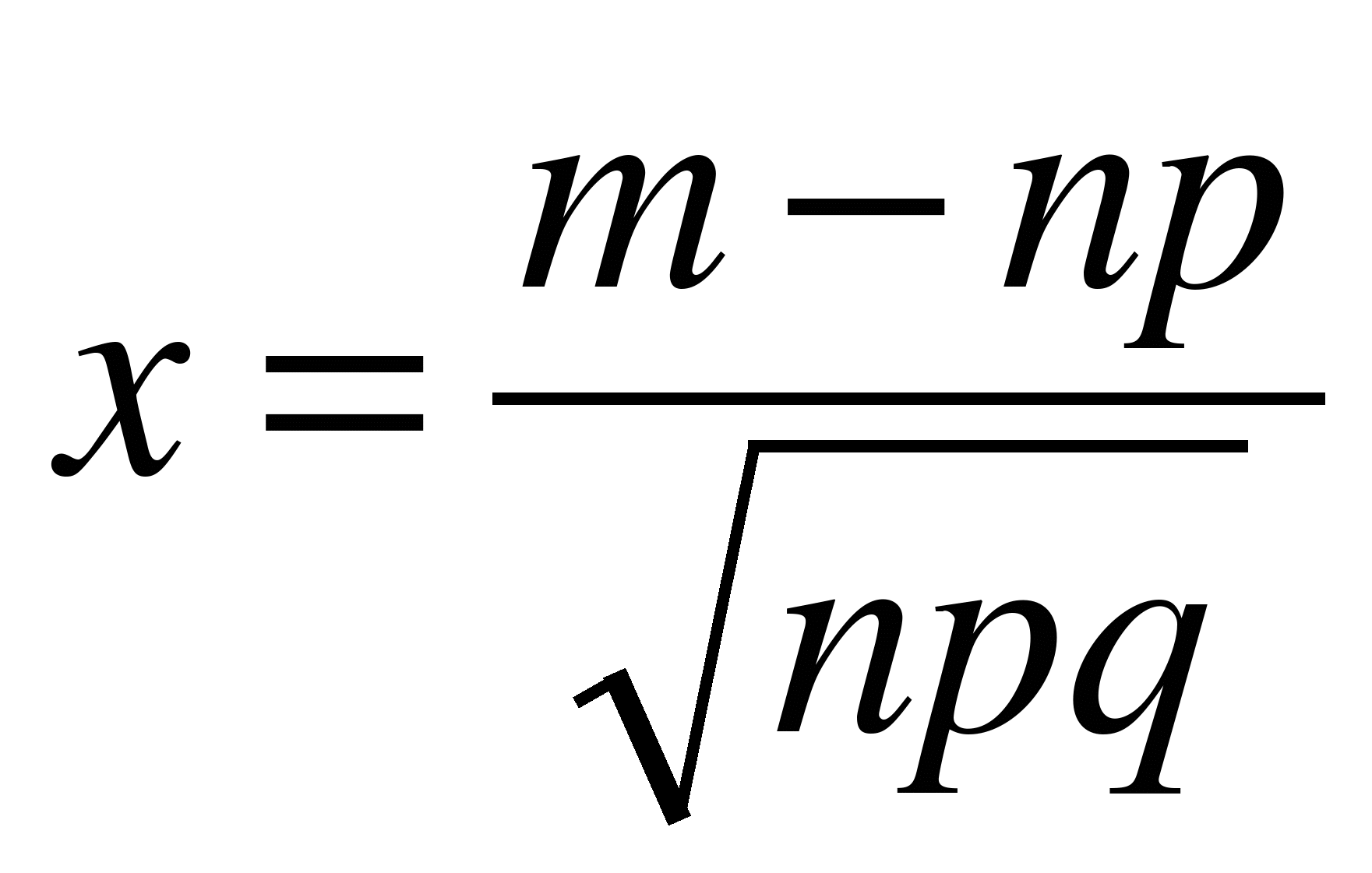

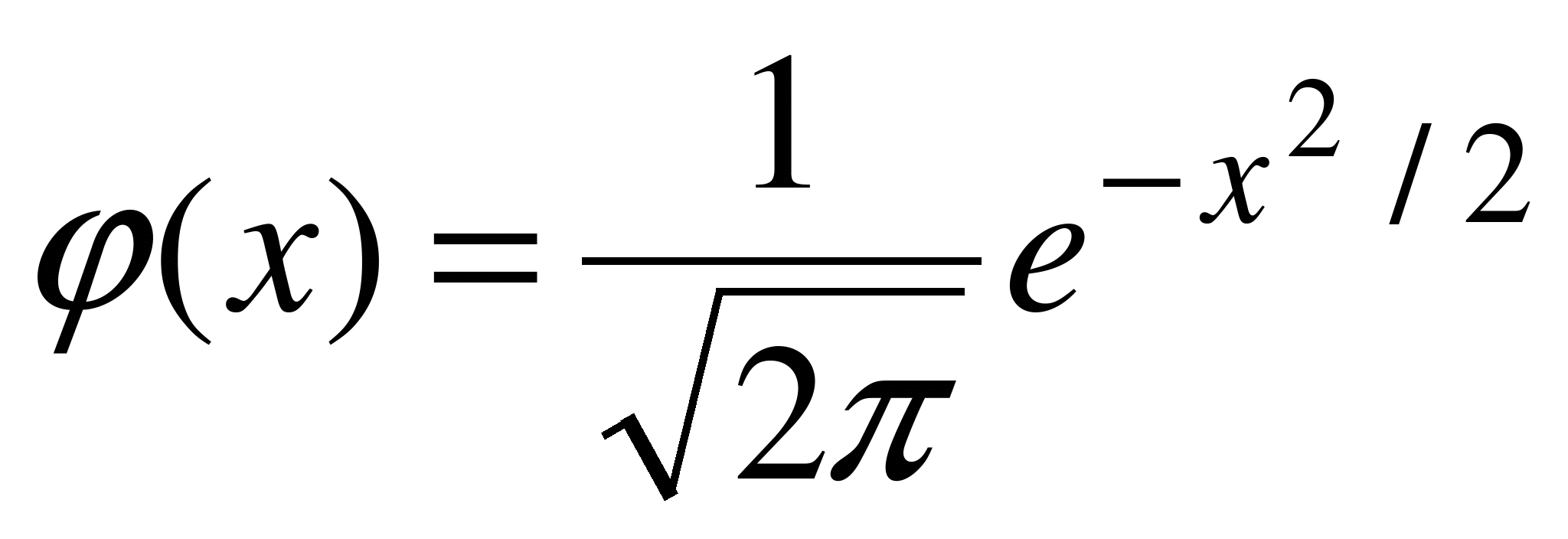Для функции 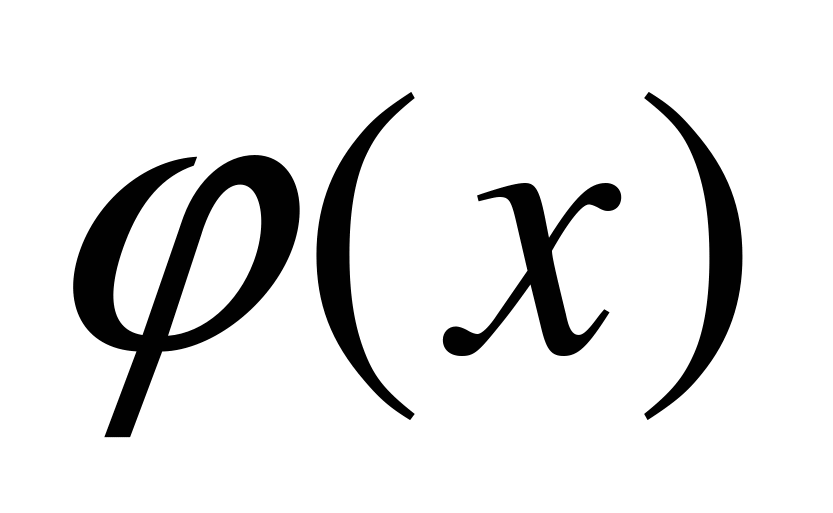составлены таблицы, которые присутствуют во всех справочниках и пособиях по теории вероятностей. Они позволяют не вычислять значение 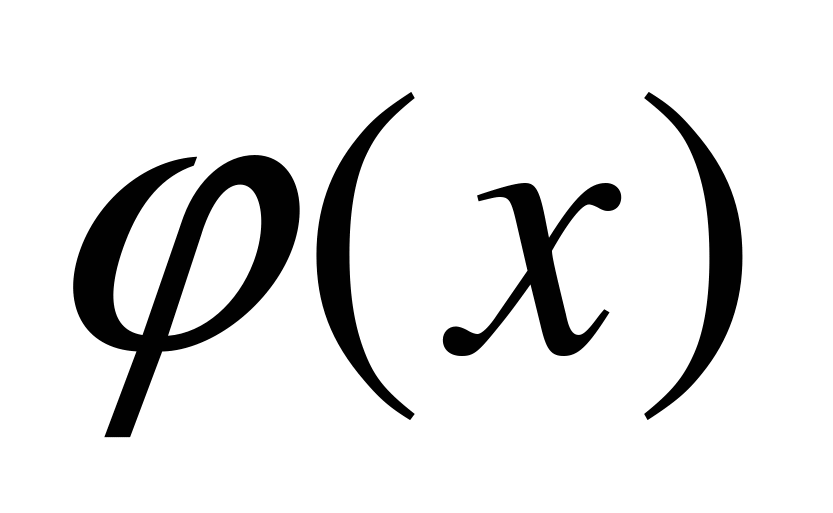в каждой конкретной задаче. При пользовании таблицами нужно учитывать, что функция 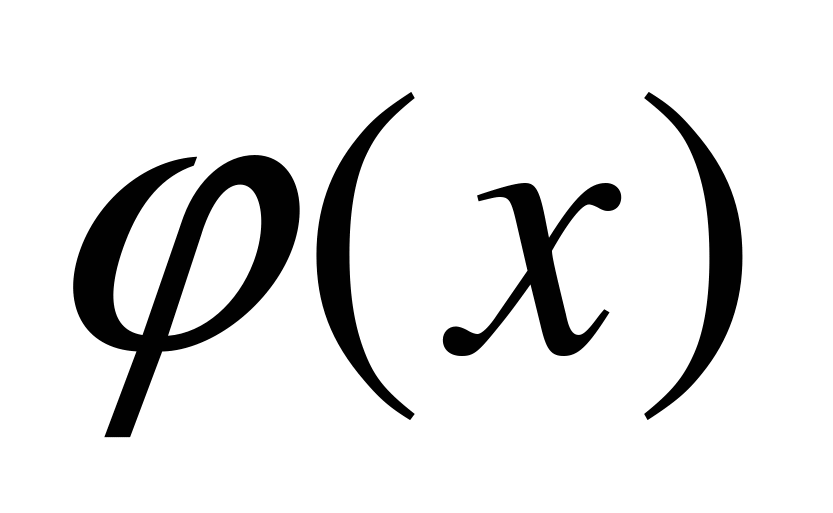четная, т.е. 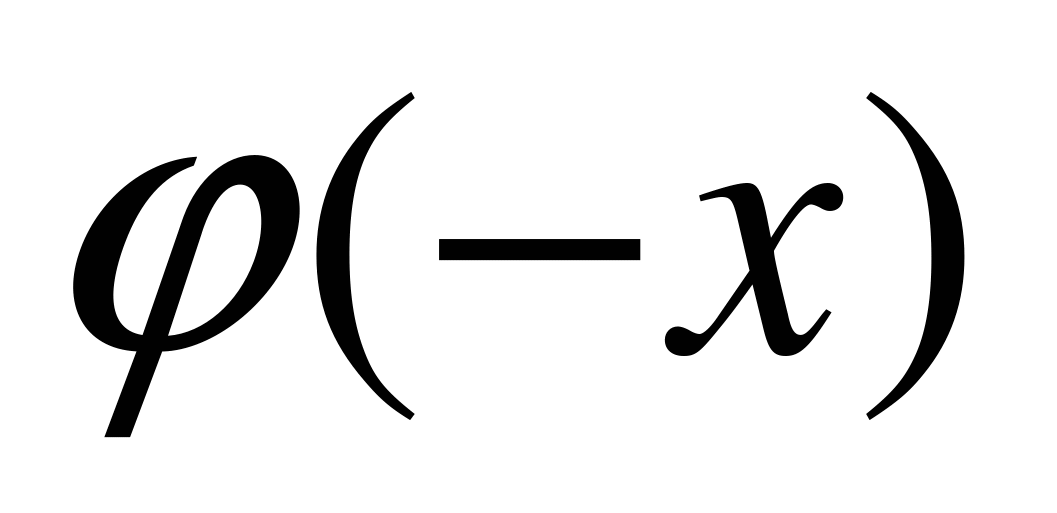= 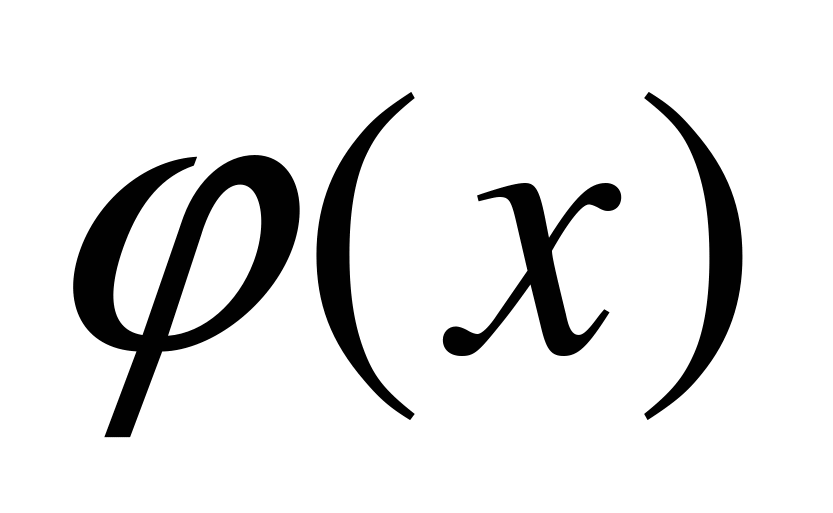. Поэтому значения этой функции при отрицательных x в таблице не приводятся.

Вы найдете таблицу значений 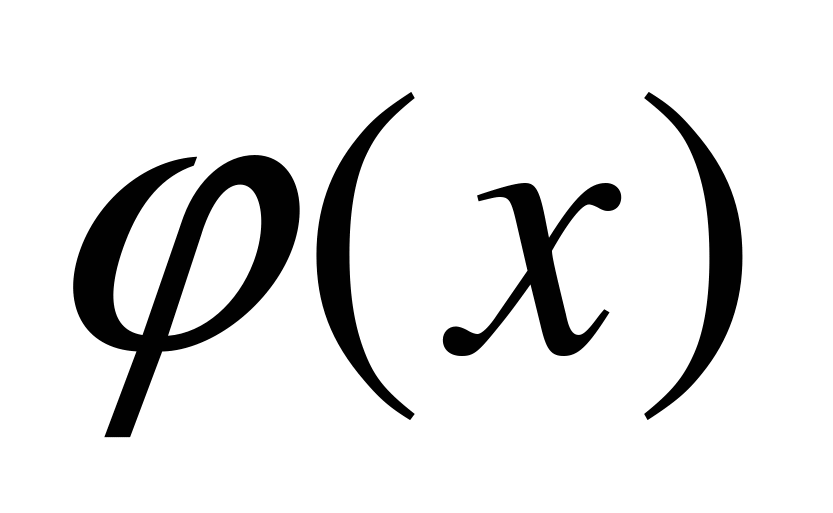в приложении, расположенном в конце данного пособия.

Формула (6.3) позволяет достаточно точно вычислить 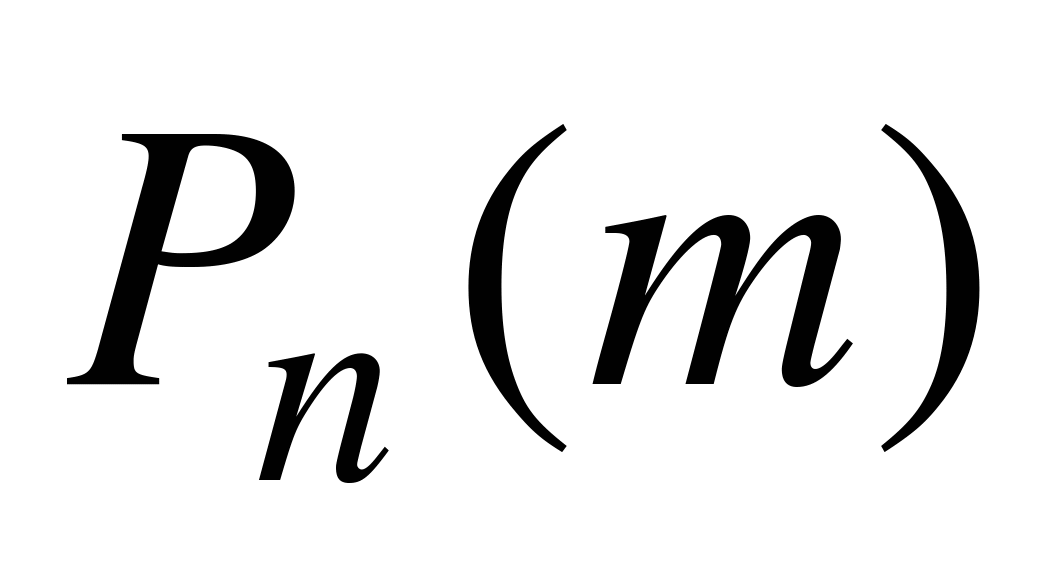, когда n велико, а p не очень близко к 0 или к 1. Этой формулой обычно пользуются, если .

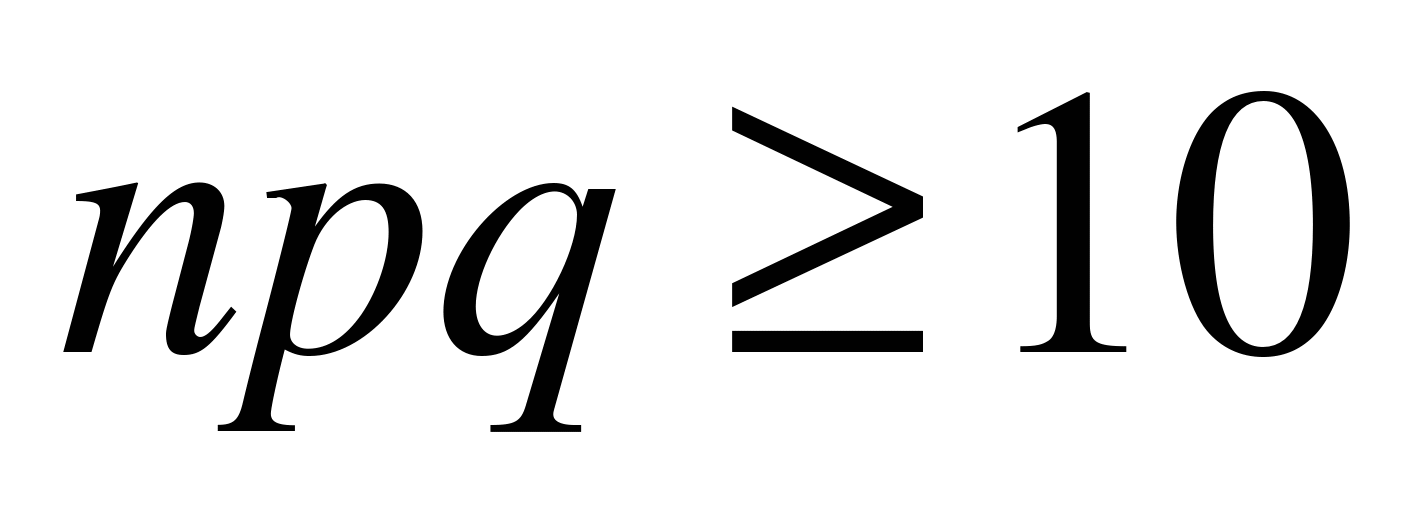Пример 6.5. 95% всей продукции некоторой фабрики составляет продукция высшего сорта. Определим вероятность того, что из взятых на проверку 500 изделий 480 окажутся высшего сорта.

По условию задачи мы находимся в рамках схемы Бернулли, где 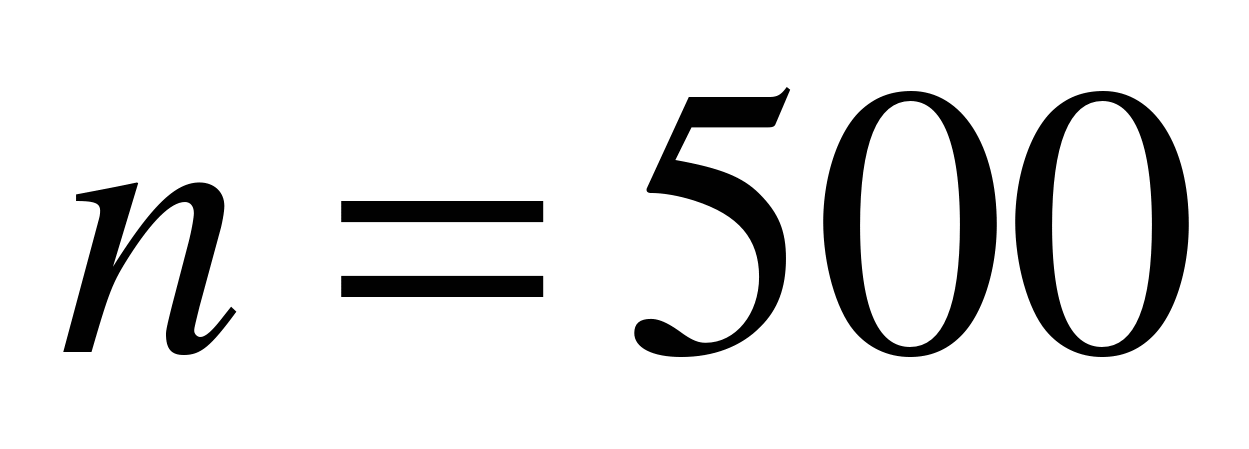, , 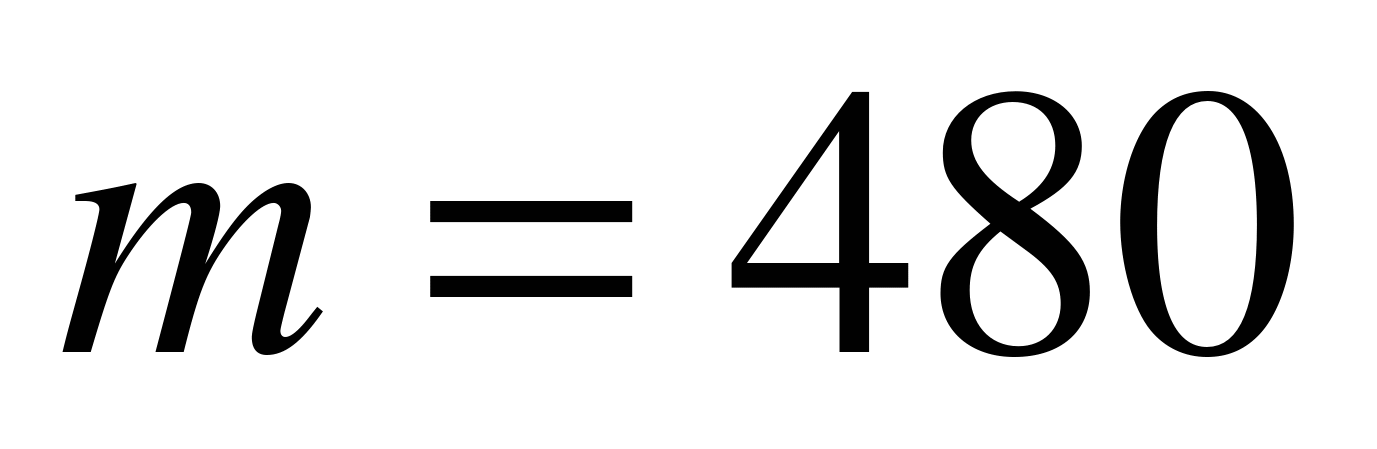, 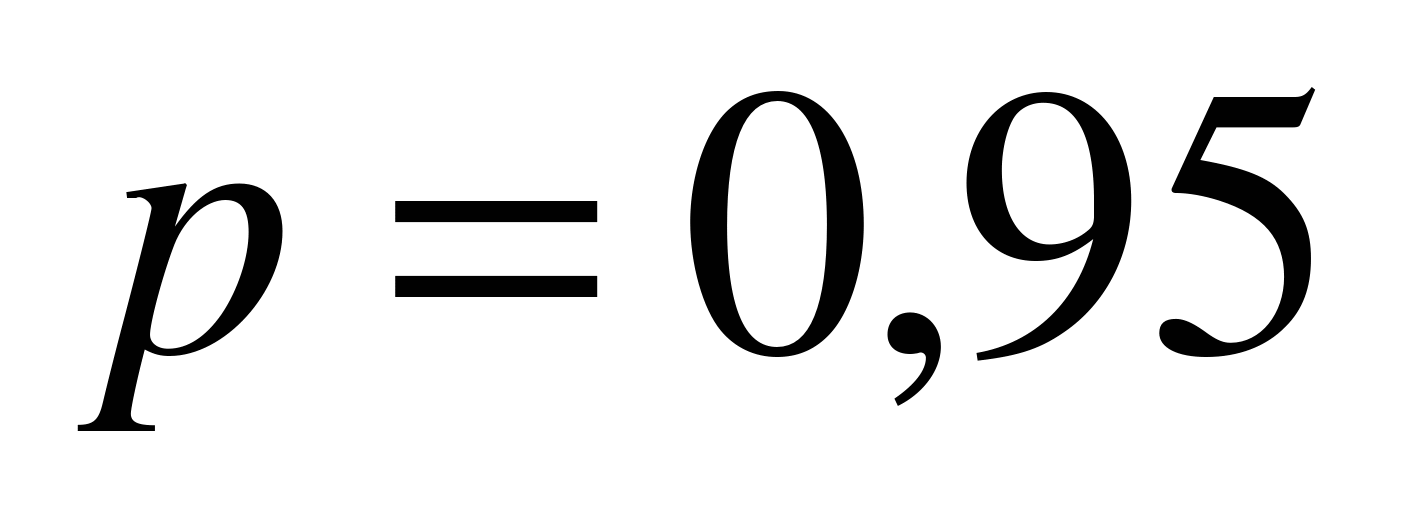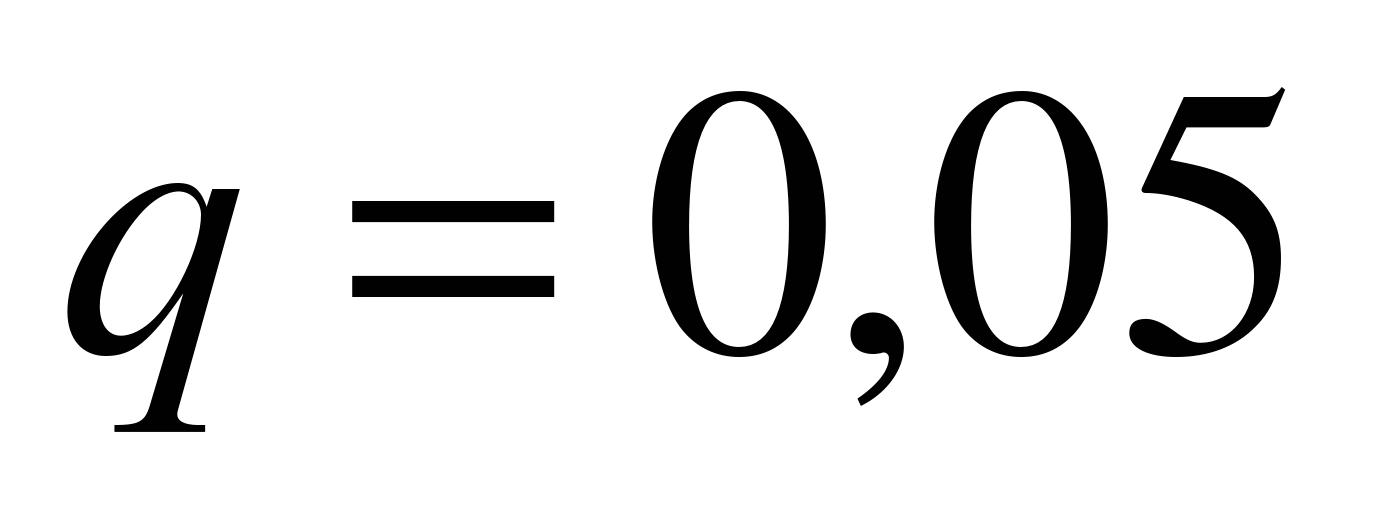. Поскольку n достаточно велико, и 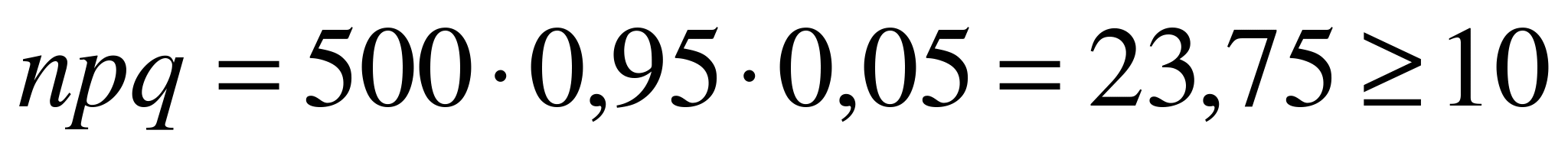, мы можем использовать формулу (6.3) для вычисления искомой вероятности. Тогда 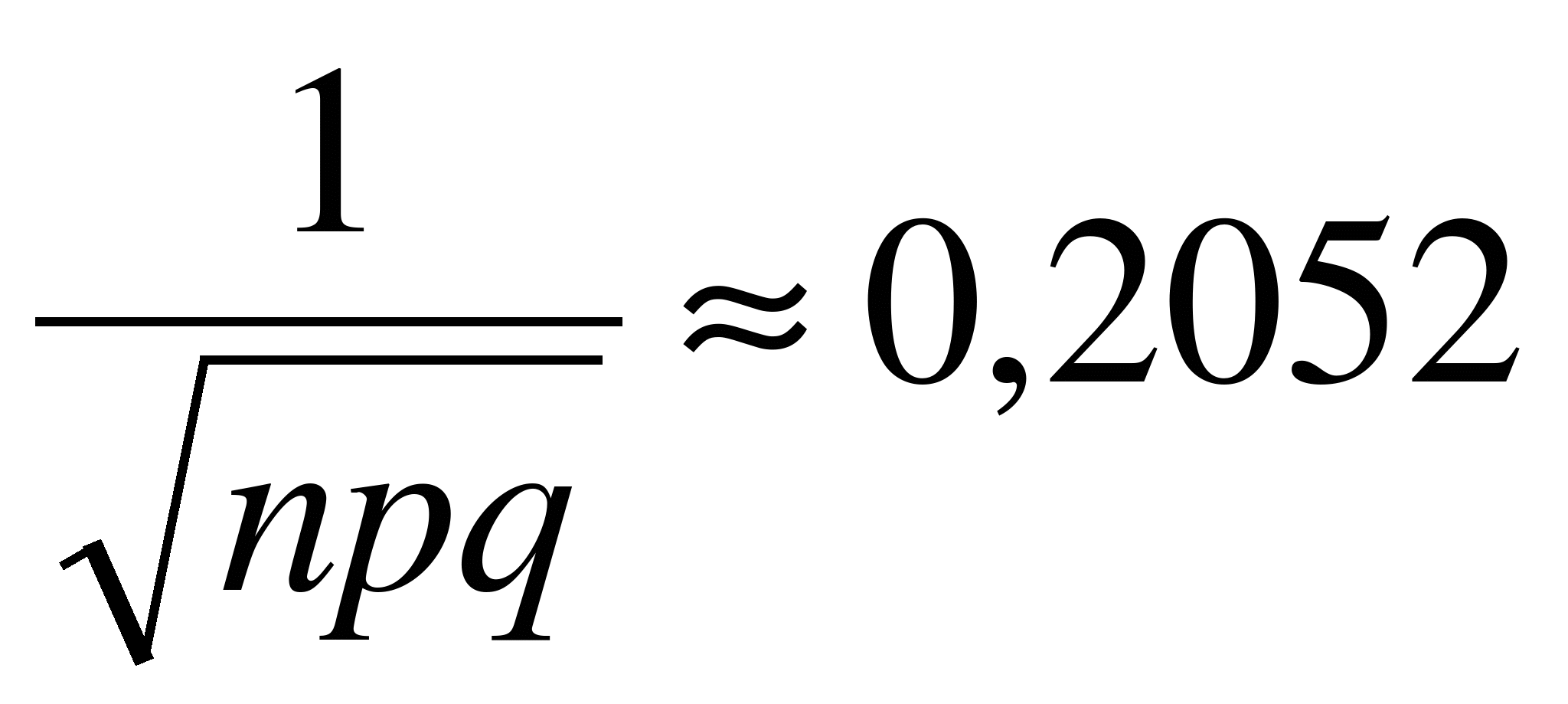, 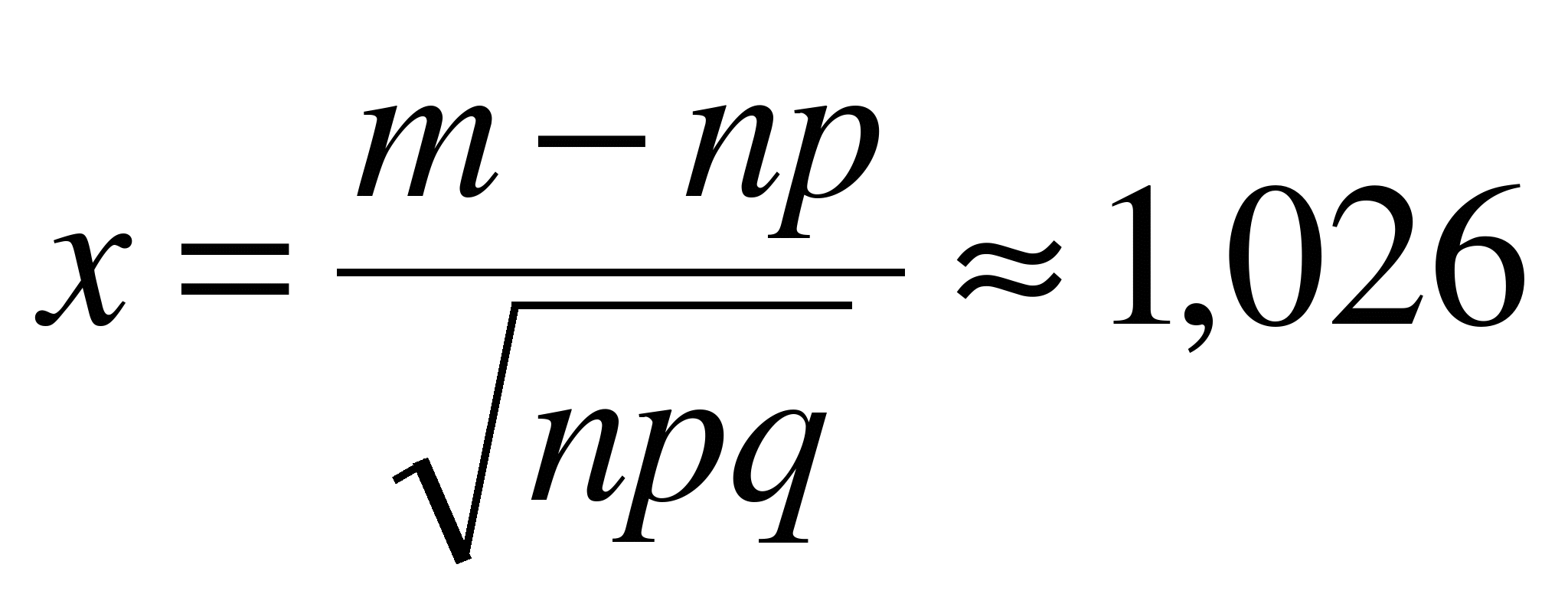. По таблице значений 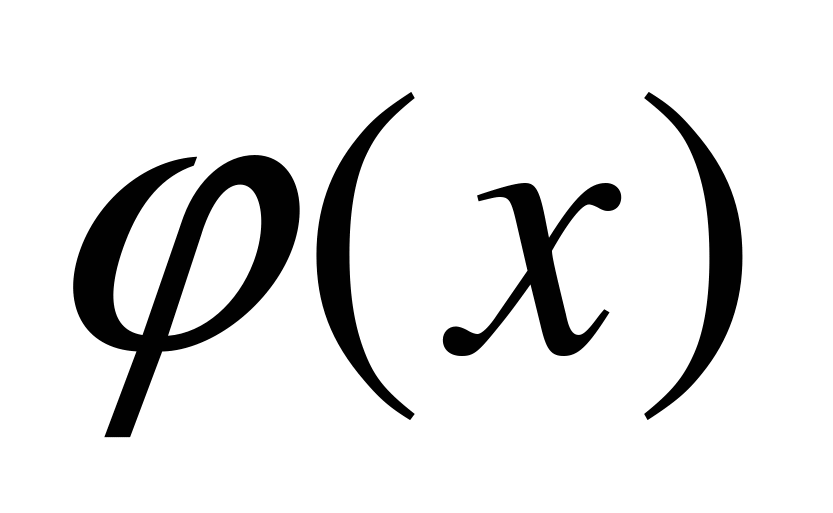находим 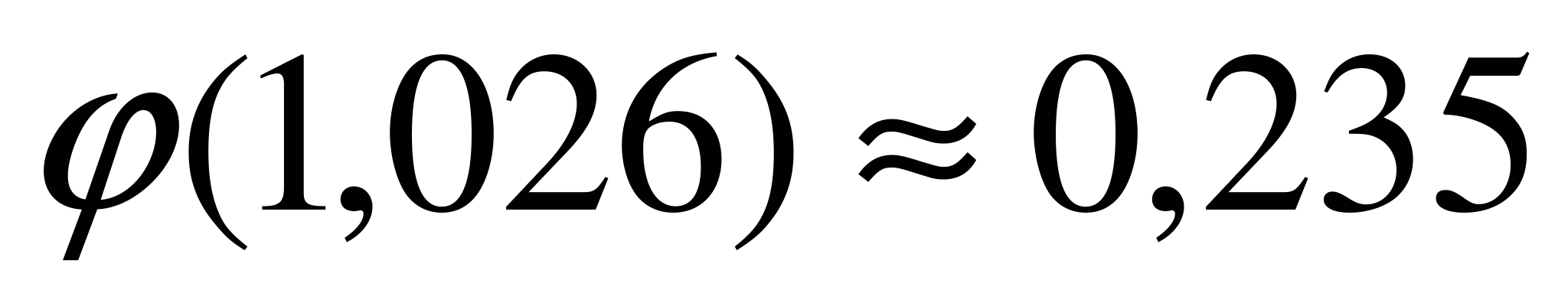. Следовательно, 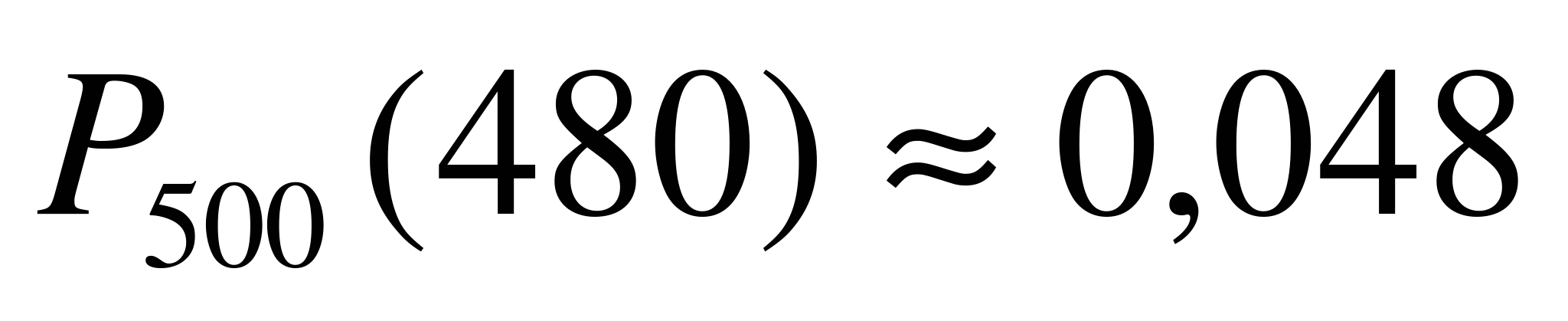. Как мы видим, полученная вероятность достаточно мала.

На практике часто в условиях схемы Бернулли требуется вычислить вероятность того, что событие А наступит не менее k₁ и не более k₂ раз, т.е. вероятность 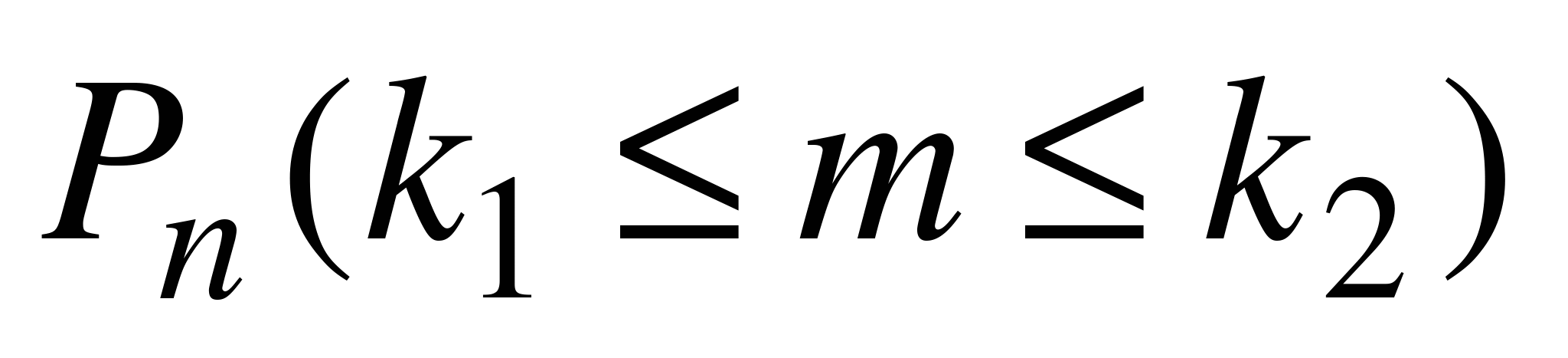. В этом случае приближенную формулу дает интегральная теорема Муавра - Лапласа.

Интегральная теорема Муавра-Лапласа.

Вусловиях схемы Бернулли т.е. при проведении n независимых испытаний с двумя исходами, в каждом из которых вероятность появления события А постоянна и равна p (0< p <1), а вероятность появления противоположного события равна q =1 –p, для 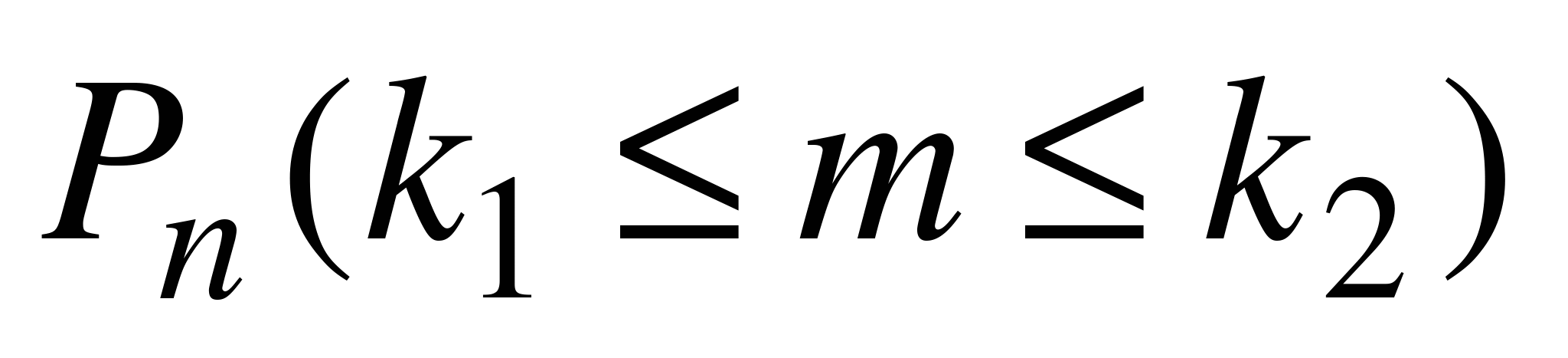(вероятности того, что в этих испытаниях событие А наступит не менее k₁ и не более k₂ раз) имеет место приближенное равенство

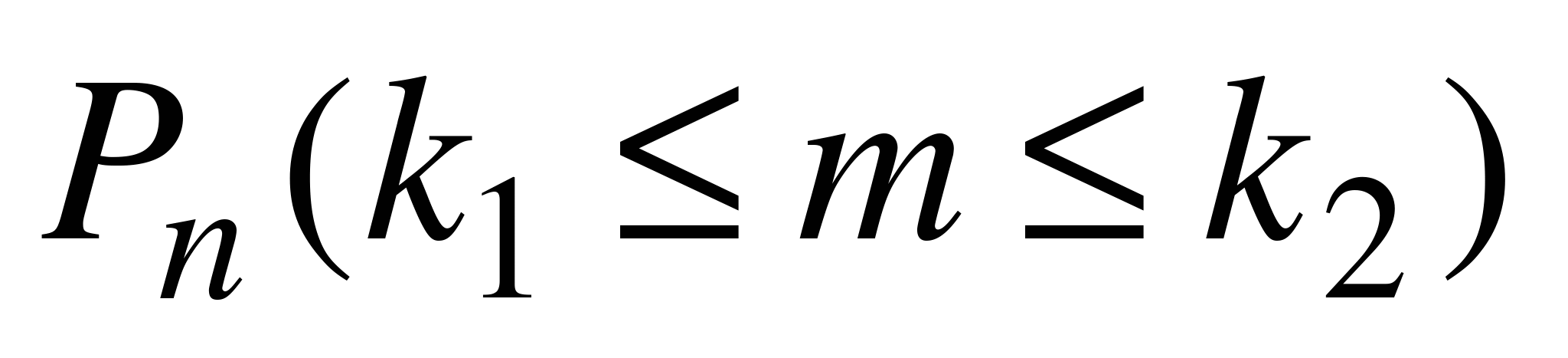
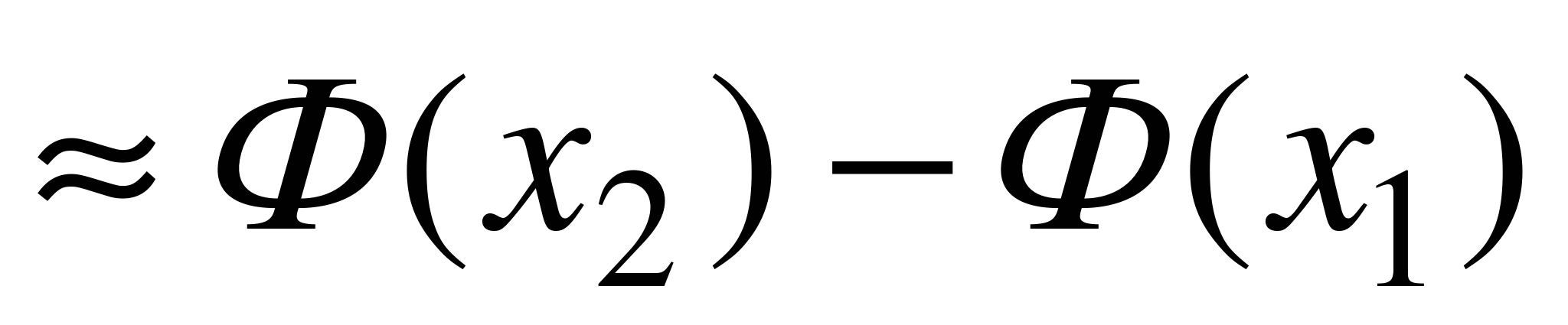, (6.4)

где , , .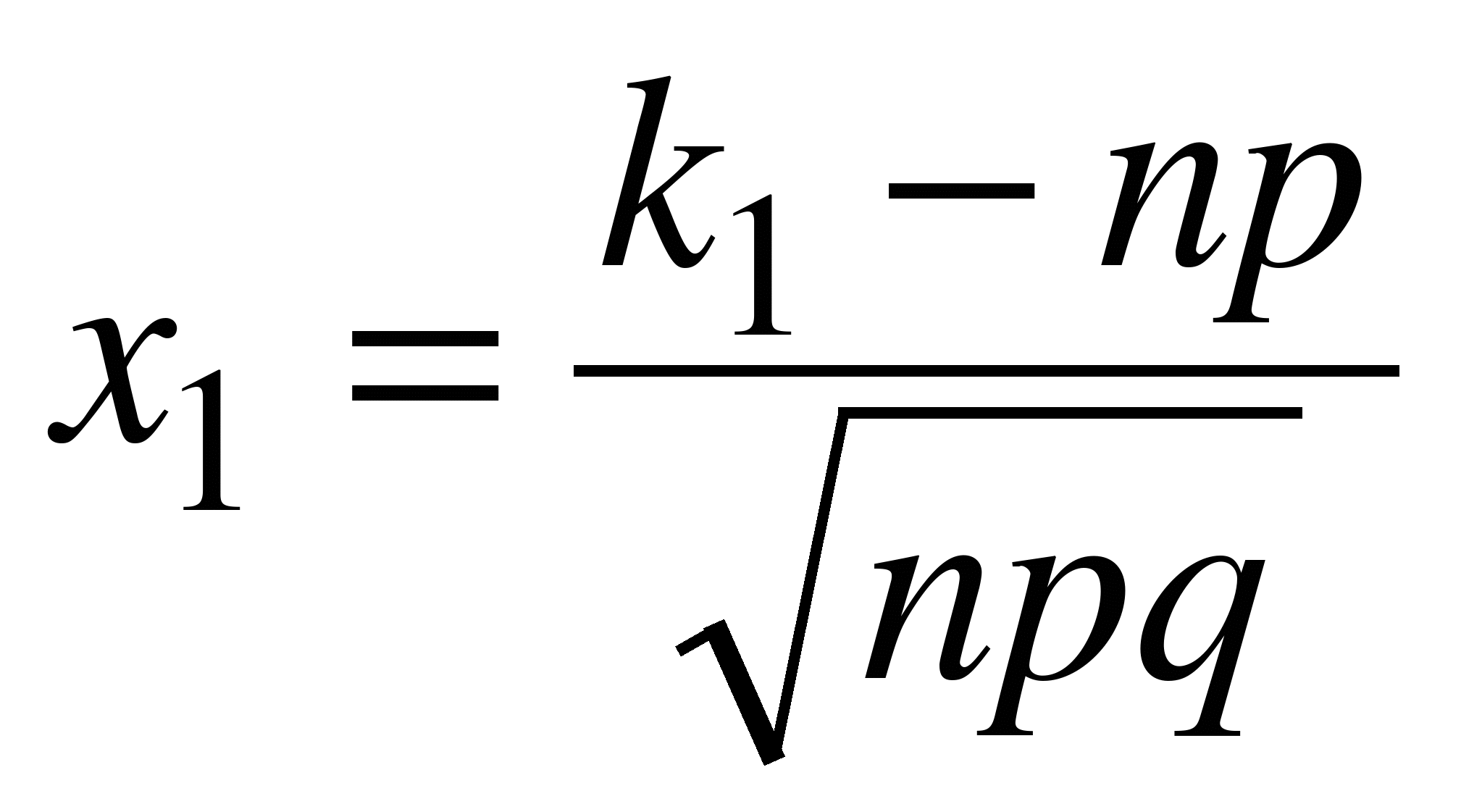

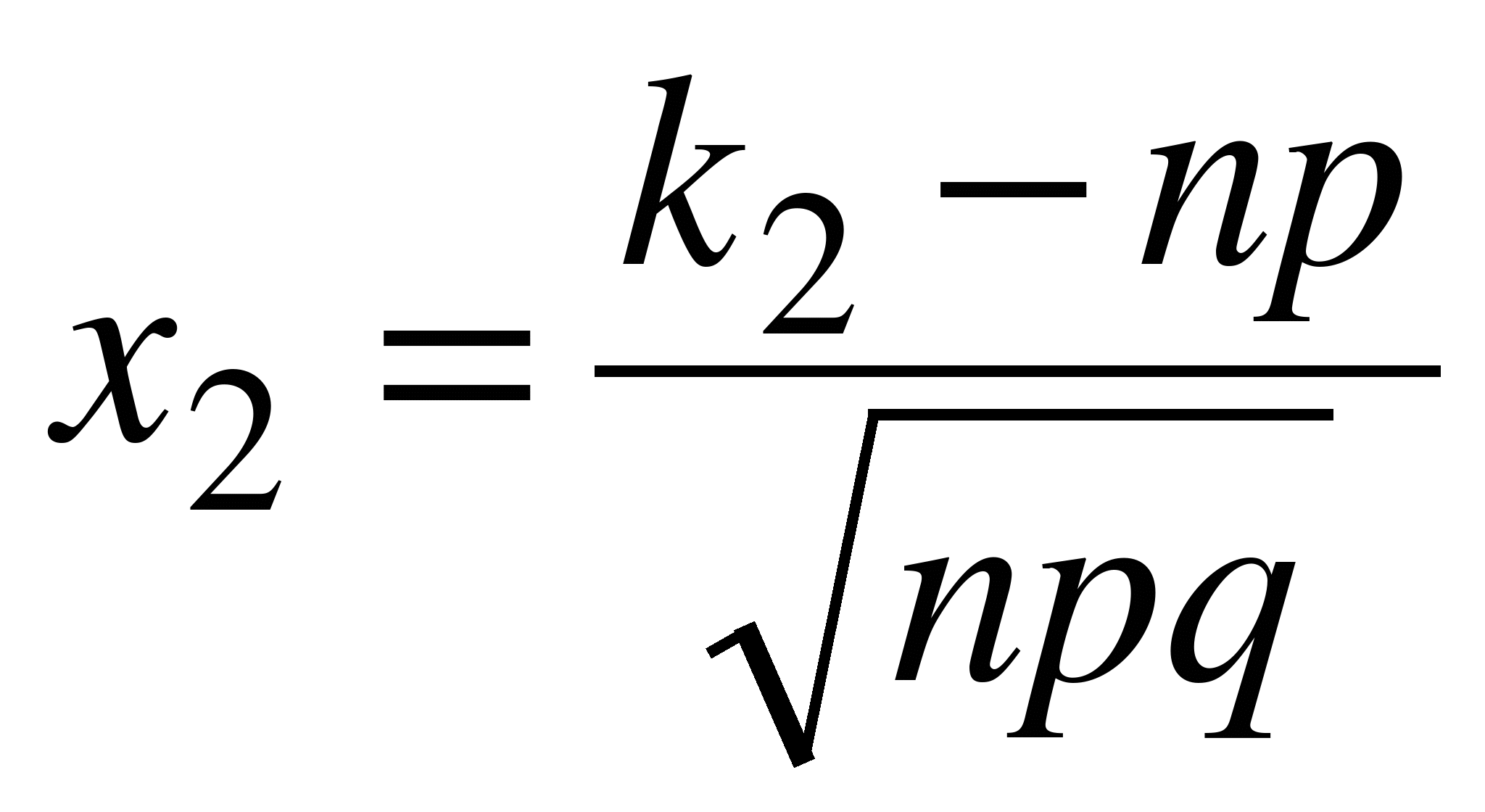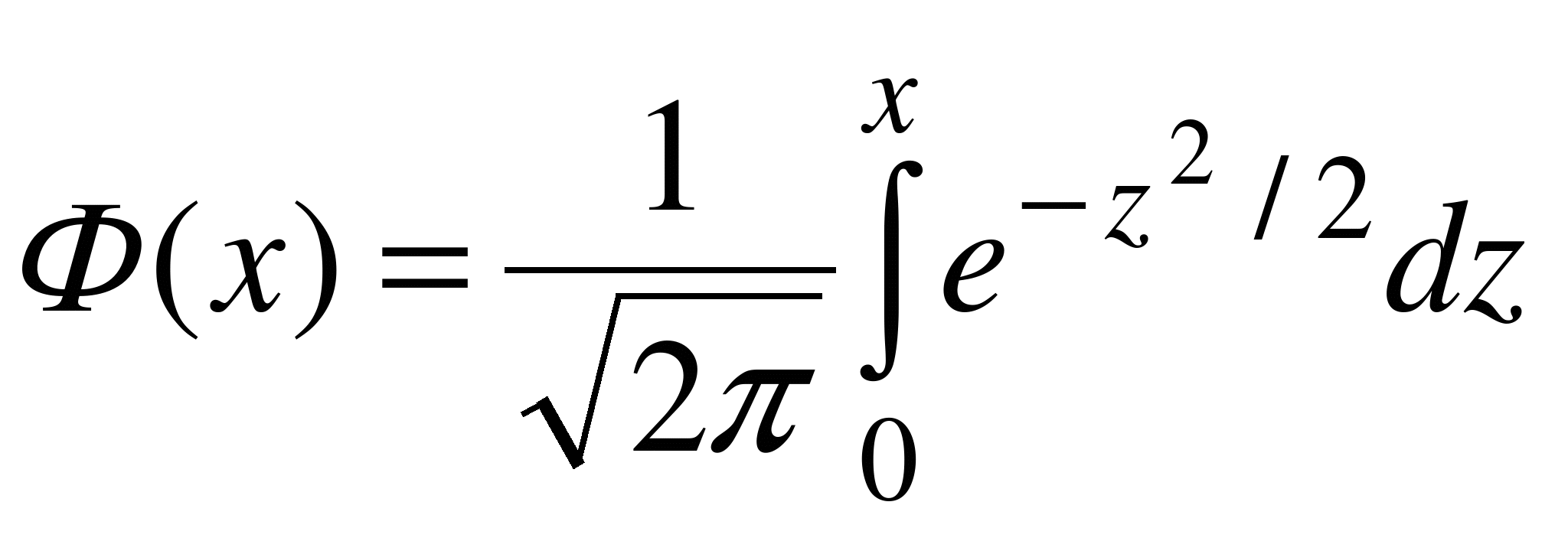Функция 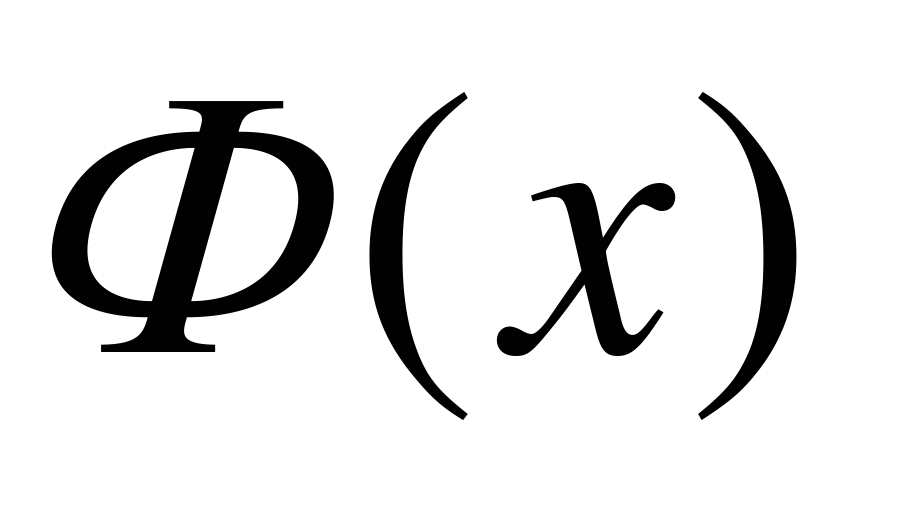называется функцией Лапласа. Для нее также составлены таблицы, которые можно найти во всех справочниках и пособиях по теории вероятностей. При пользовании таблицами нужно учитывать, что функция 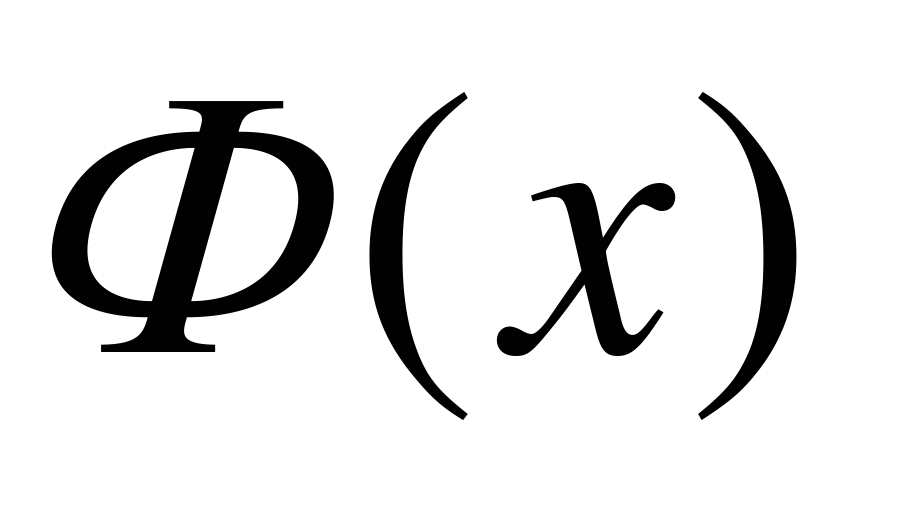нечетная, т.е. 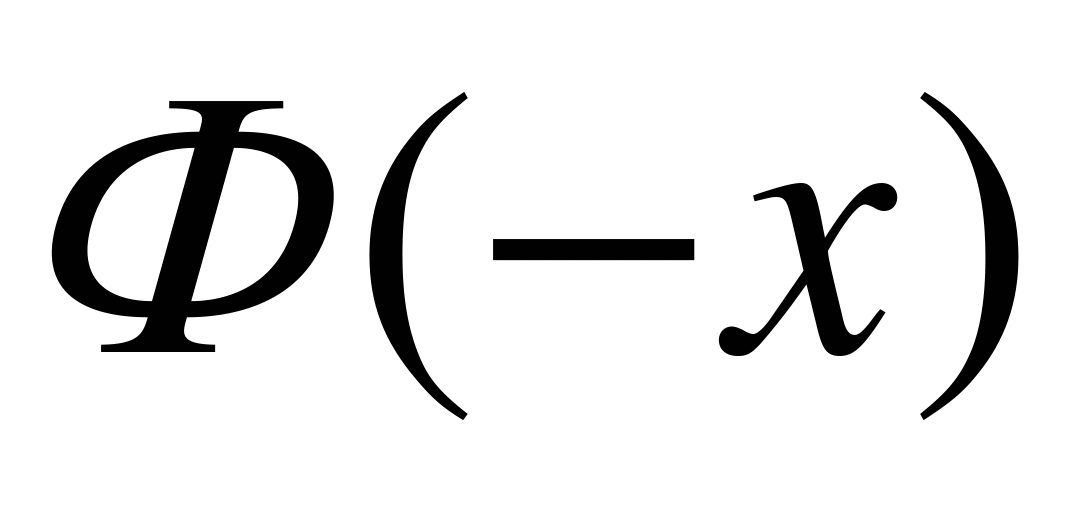= 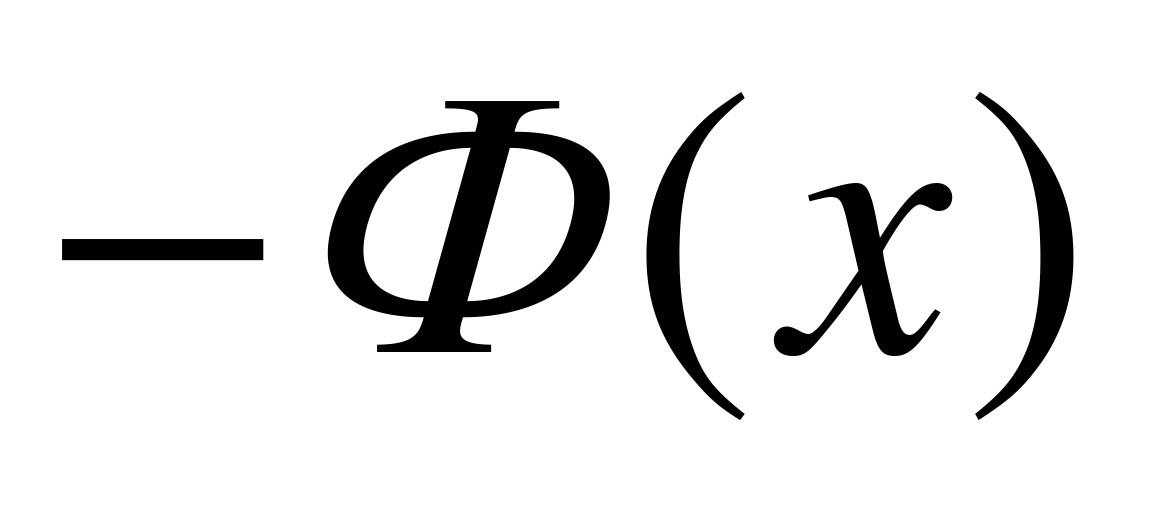. Кроме того, обычно в таблицах указаны значения функции Лапласа для значений x от 0 до 5; при x > 5 полагают 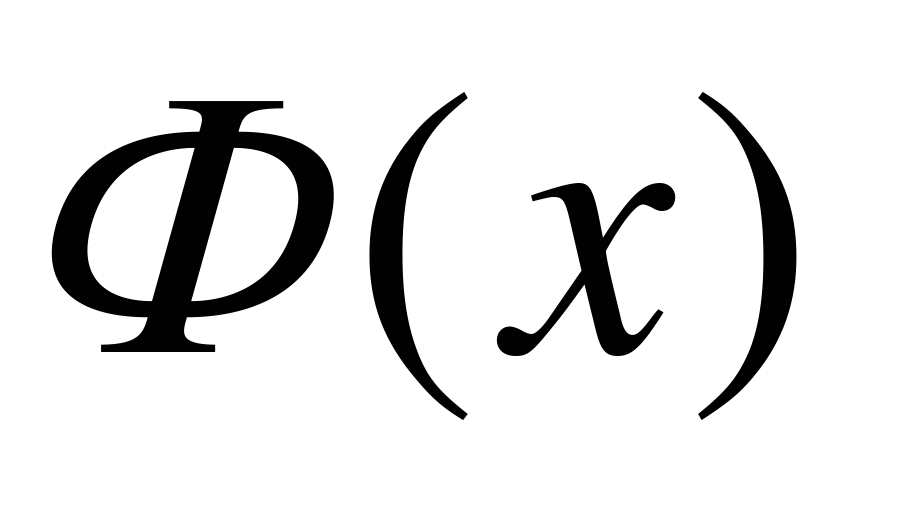=0,5.

Таблицу значений 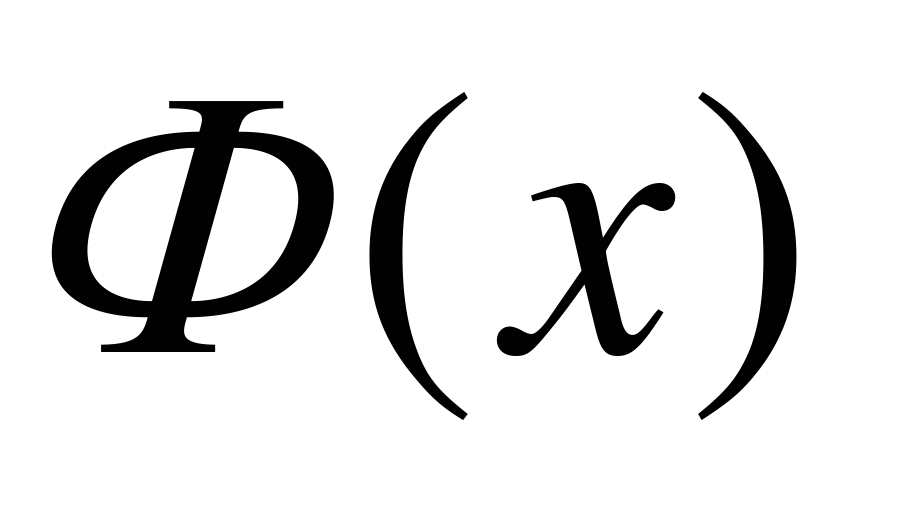Вы также найдете в приложении.

Замечание. В некоторых учебниках функцией Лапласа называют функцию 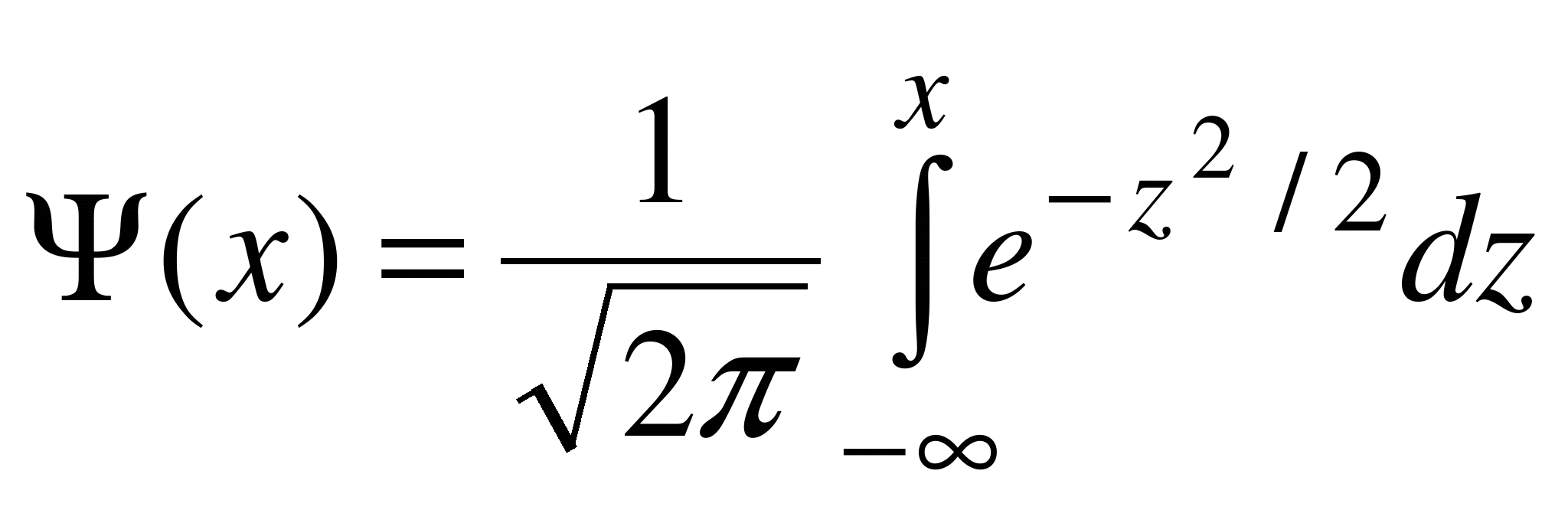(от функции 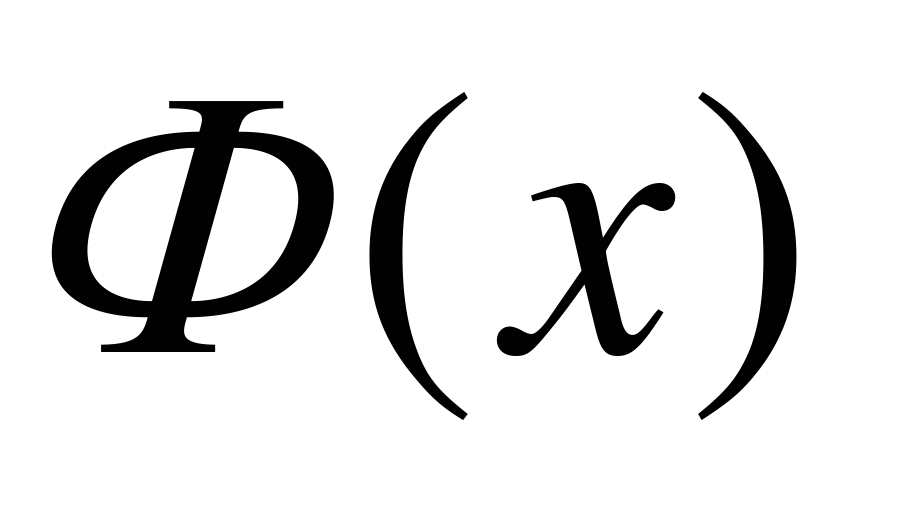она отличается нижним пределом интегрирования). При этом все формулы интегральной теоремы сохраняются, таблицы для вычисления 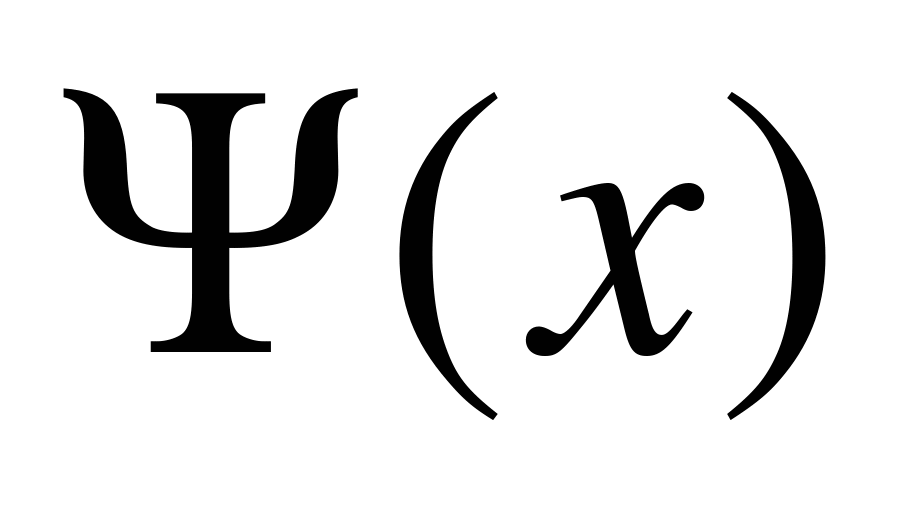приводятся в этих учебниках, но функция 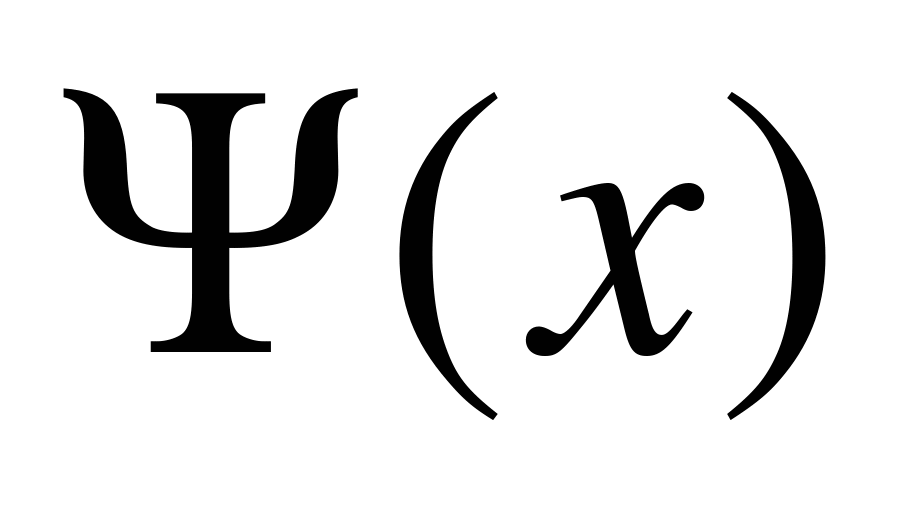не обладает свойством нечетности. Для вычисления значений 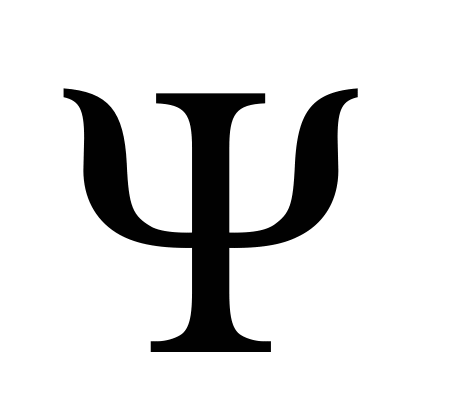при отрицательных x нужно использовать соотношение .

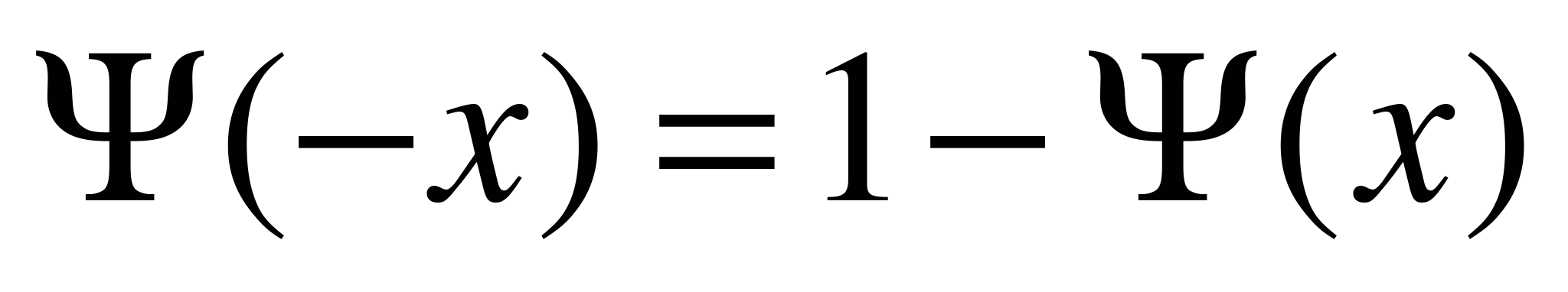Пример 6.6. В условиях примера 5.5 найдем вероятность того, что от 470 до 490 изделий окажутся высшего сорта.

По условию задачи 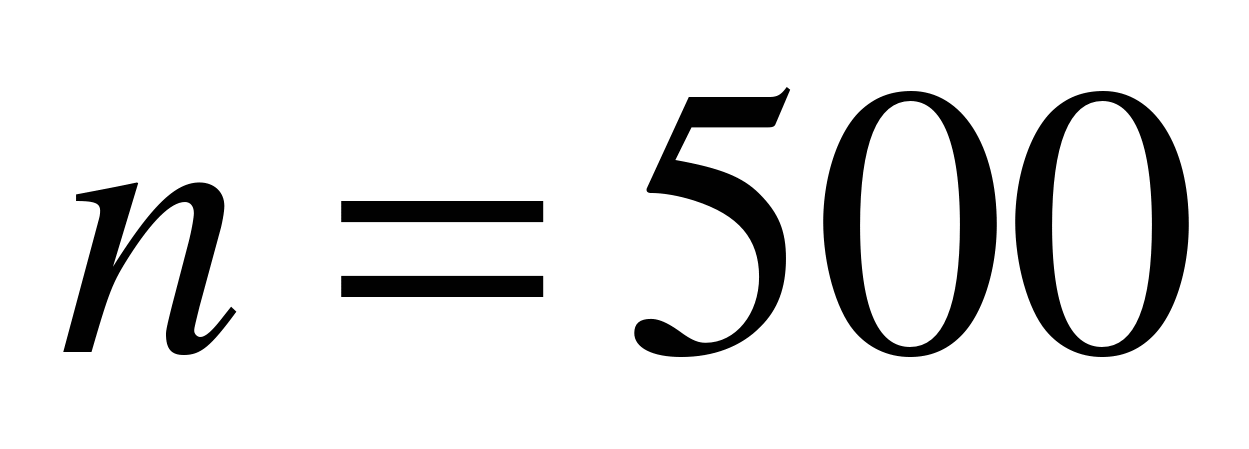, k₁ =470, k₂ =490, 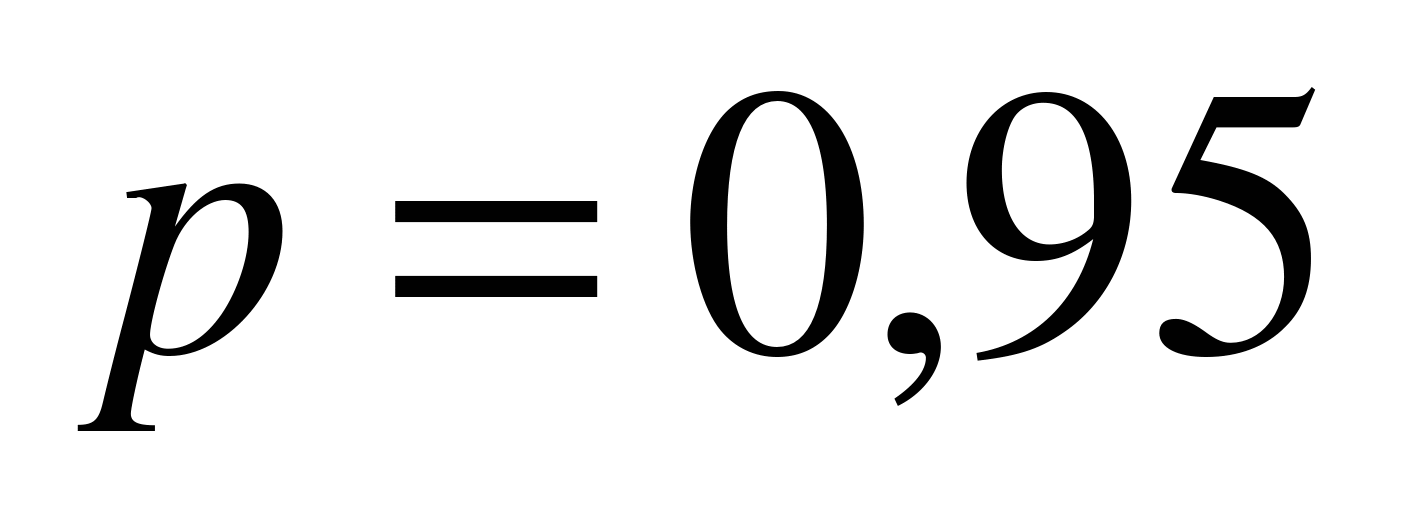, 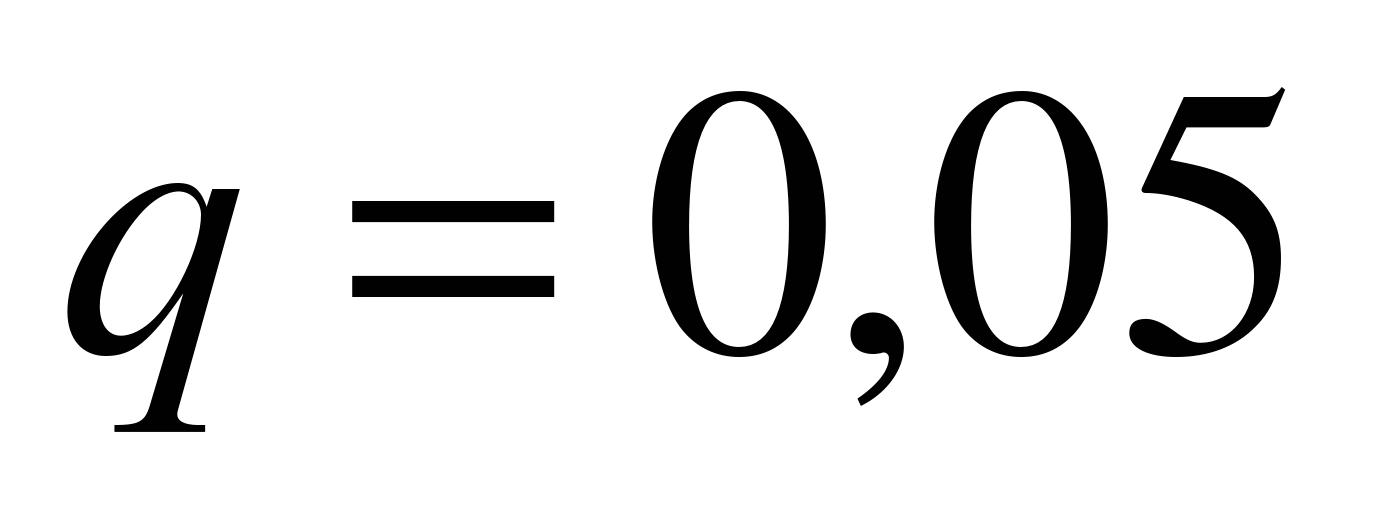. Поскольку n достаточно велико, и 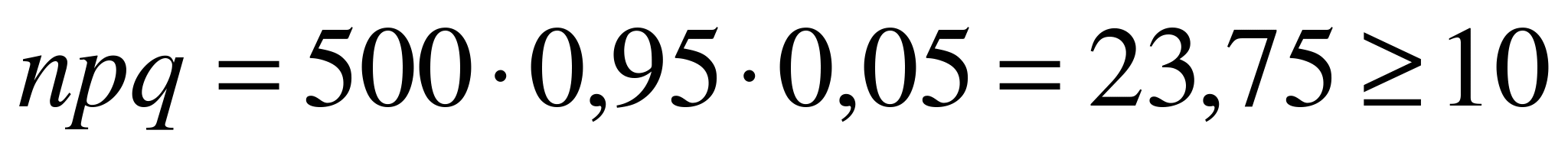, мы для вычисления искомой вероятности 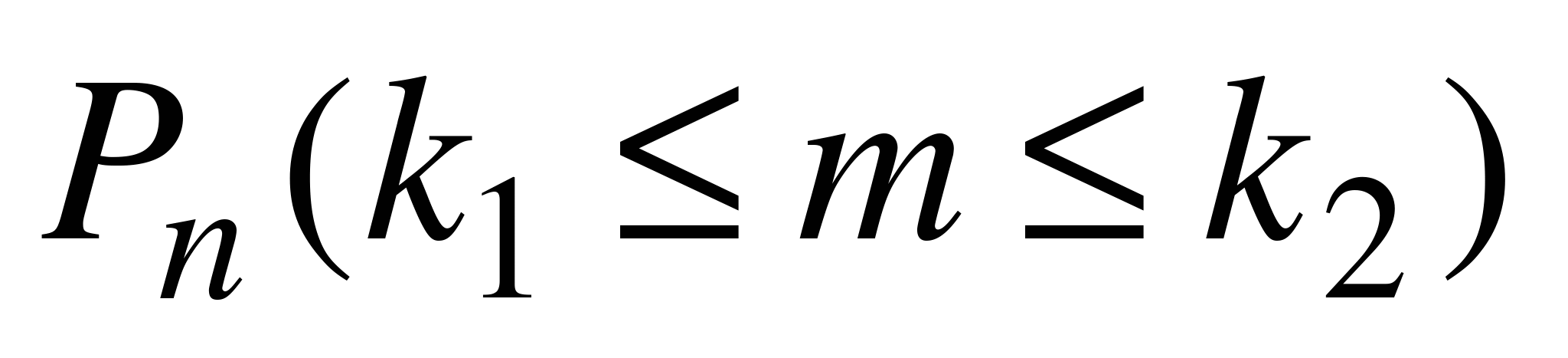используем формулу (6.4). Проводя вычисления, получаем: 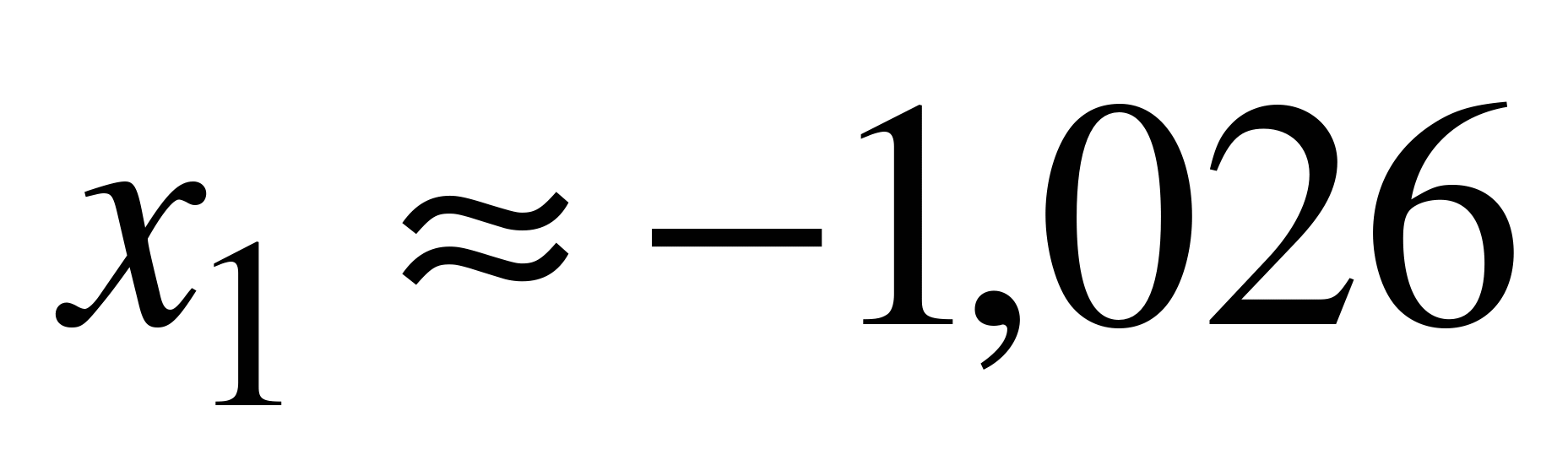, 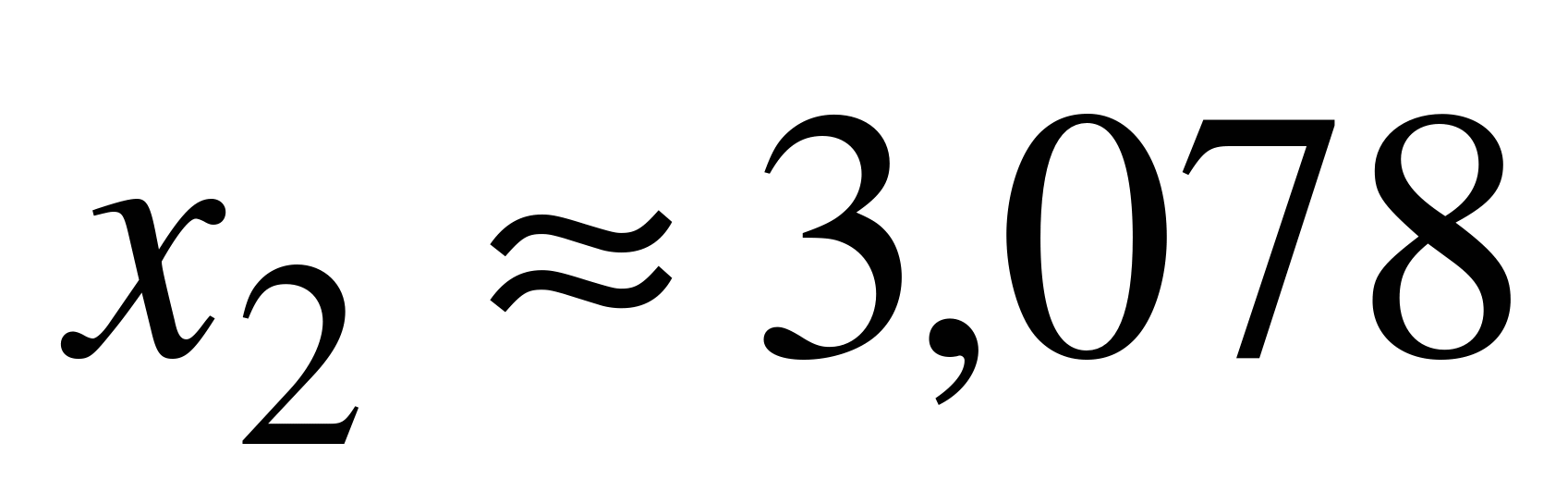. По таблице значений функции Лапласа 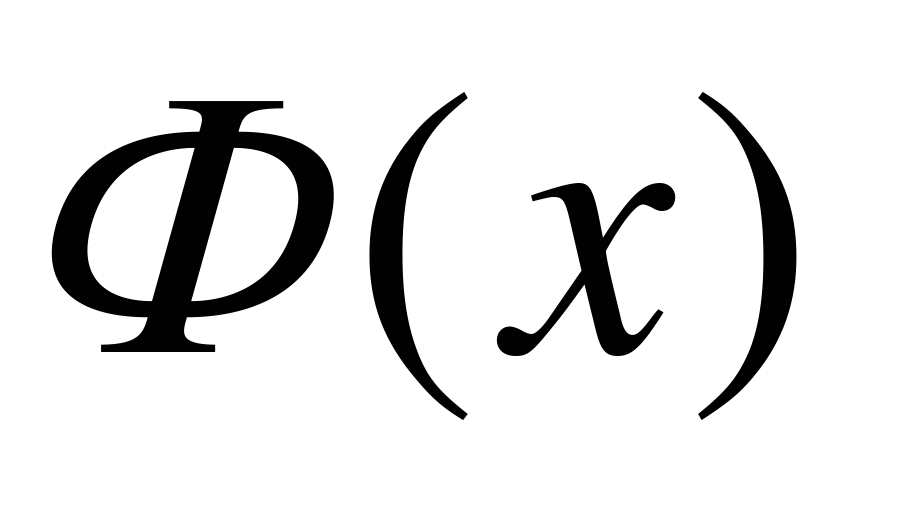находим , .

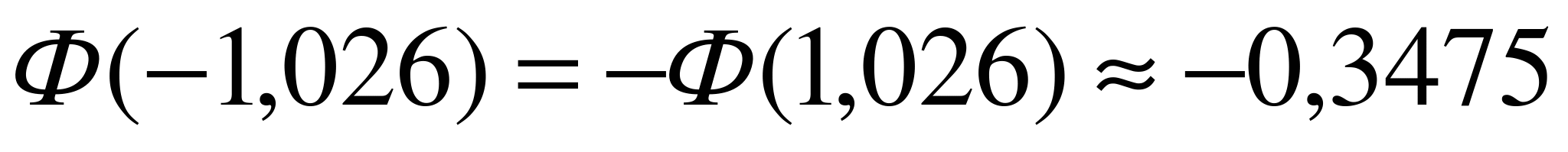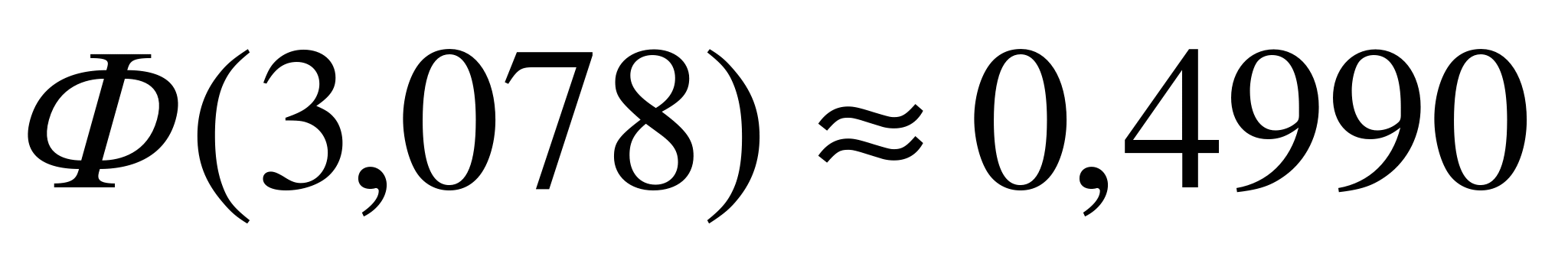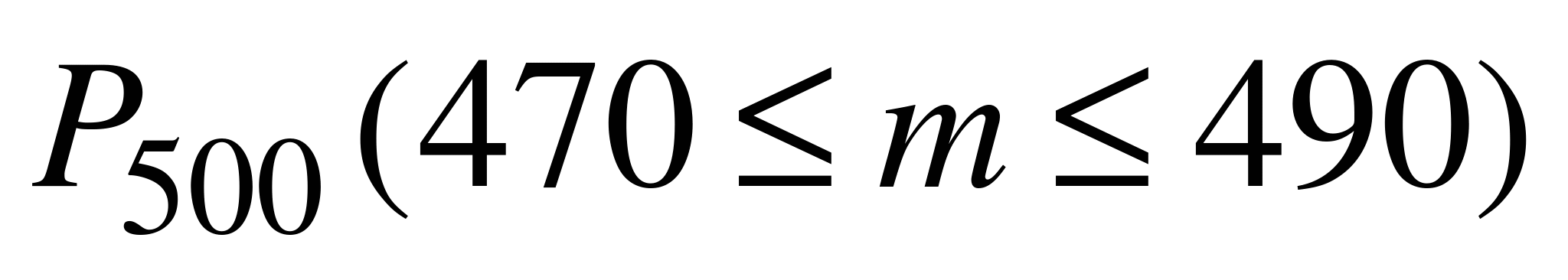
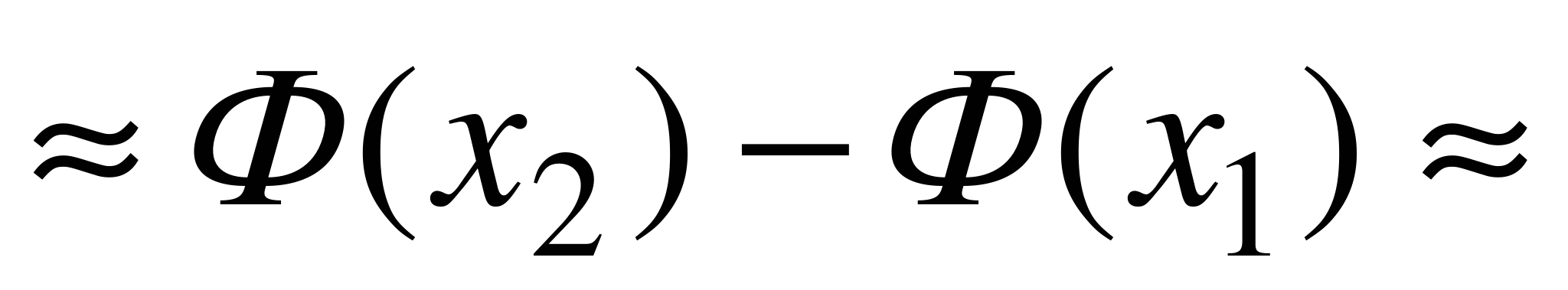
Следовательно, 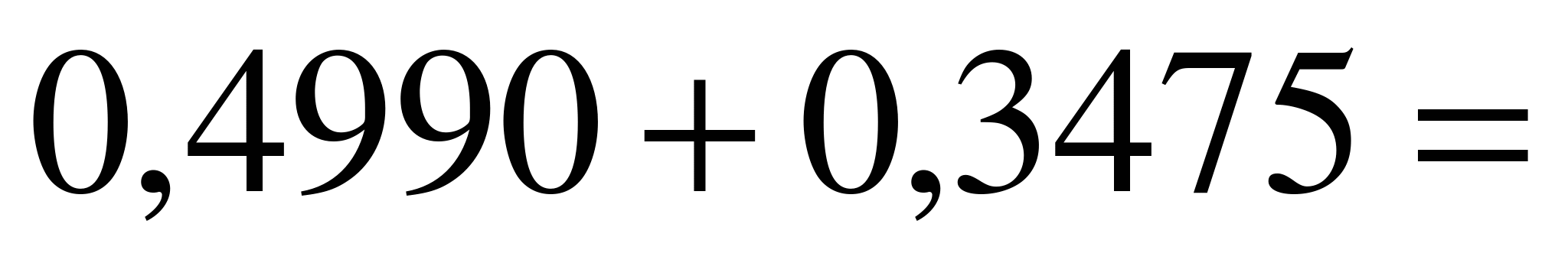0,8465.

Доказательства локальной и интегральной теорем Лапласа достаточно сложны и объемны, поэтому мы привели здесь лишь формулировки теорем и примеры, иллюстрирующие их использование.

Приведем также одно важное следствие из интегральной теоремы Муавра-Лапласа, а именно формулу для вычисления вероятности осуществления неравенства 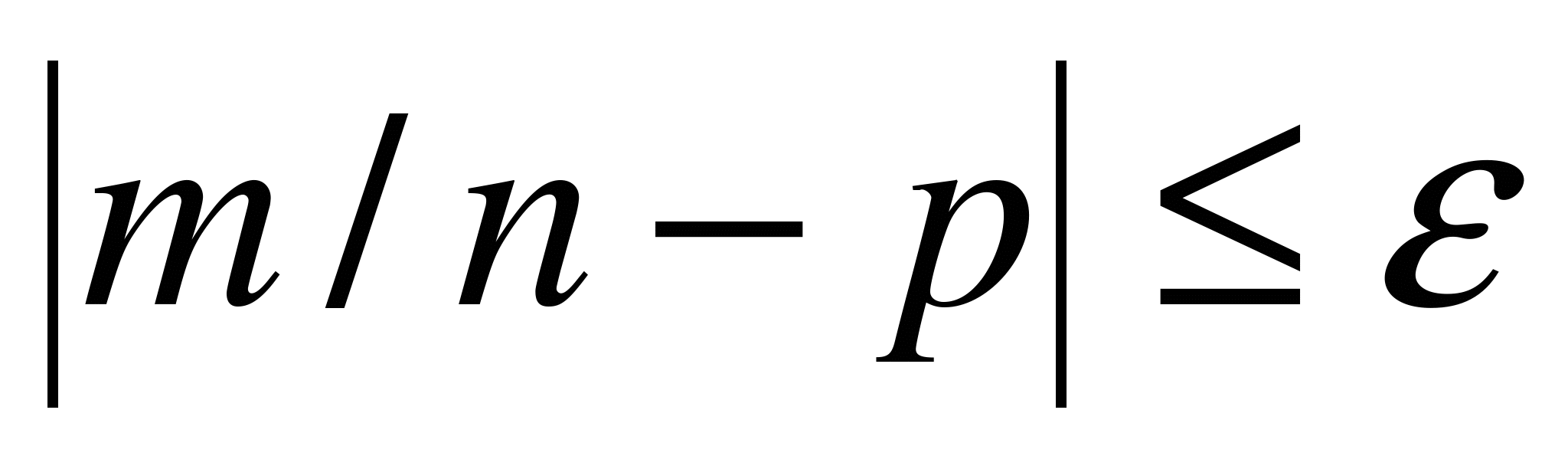, то есть вероятности того, что отклонение относительной частоты m/n наступления события А от его вероятности p не превышает по абсолютной величине некоторого заданного числа e:

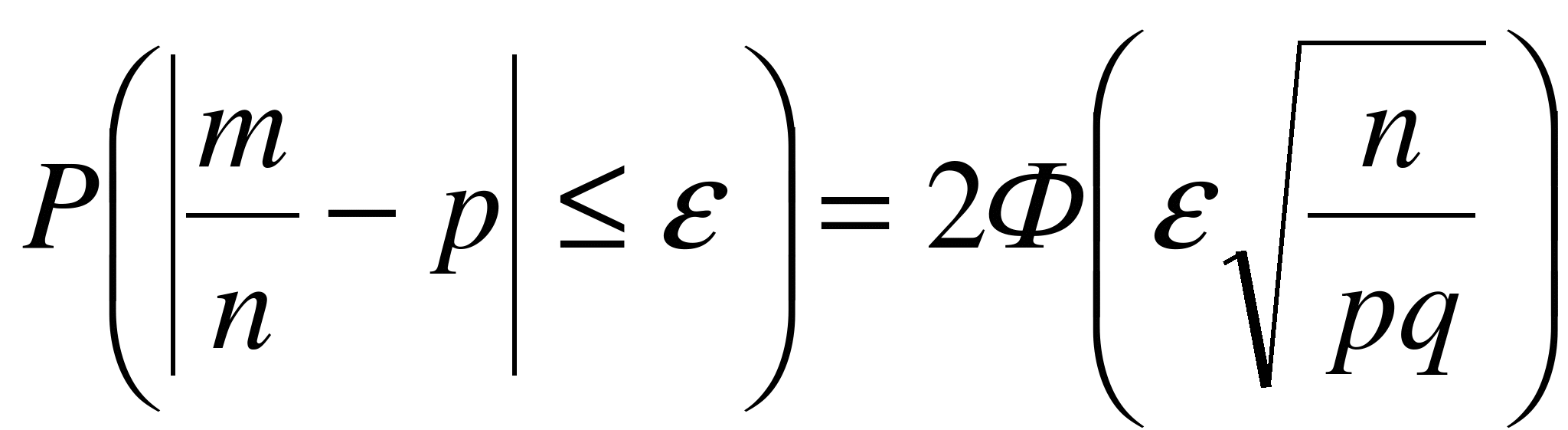. (6.5)

Равенство (6.5) легко выводится из (6.4) и носит название формулы вероятности отклонения относительной частоты от постоянной вероятности в независимых испытаниях.

Пример 6.7. Вероятность появления события А в каждом из независимых испытаний равна 0,6. Найдем вероятность того, что относительная частота появления события А в 1000 испытаниях отклонится от его вероятности по абсолютной величине не более, чем на 0,02.

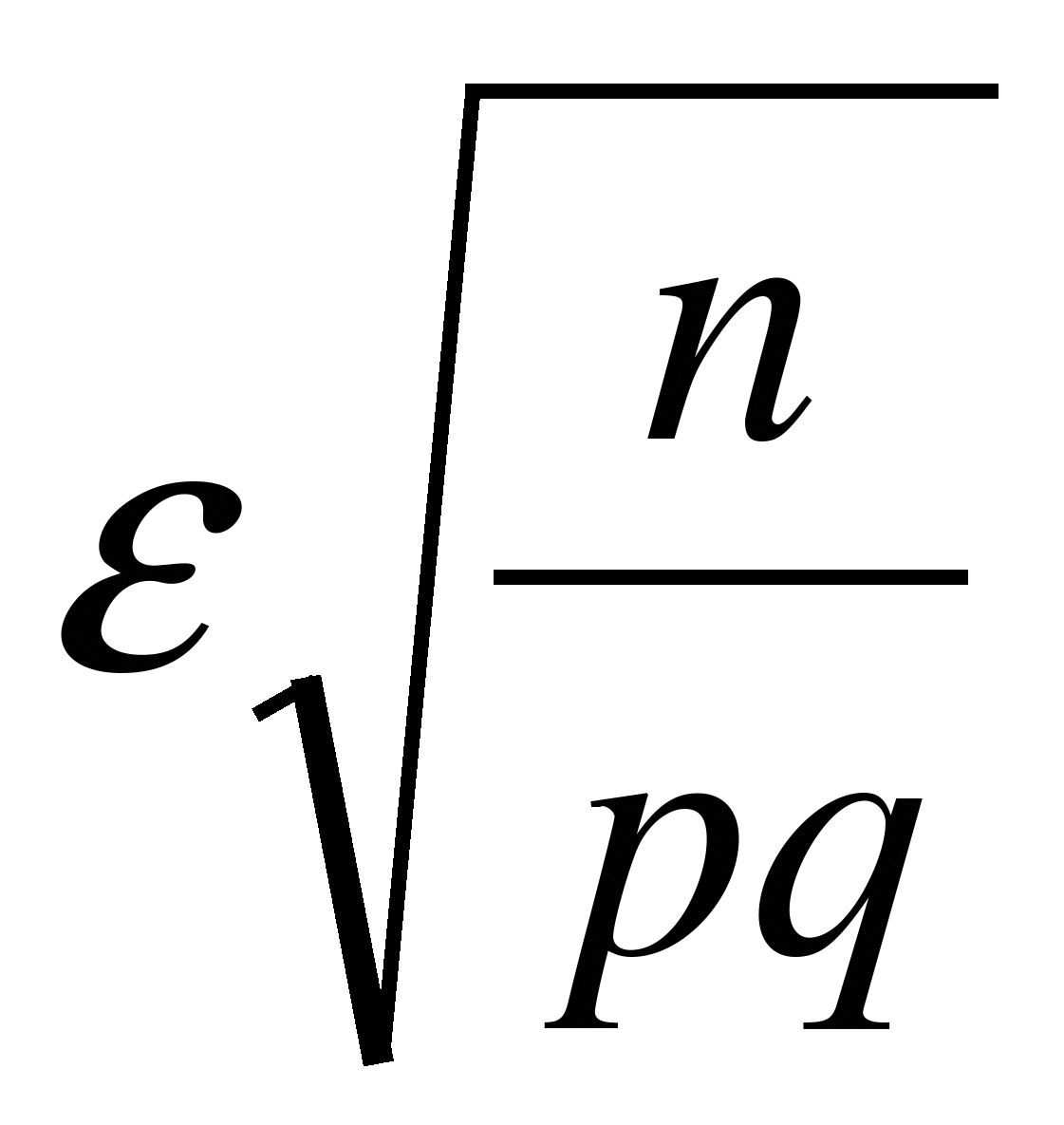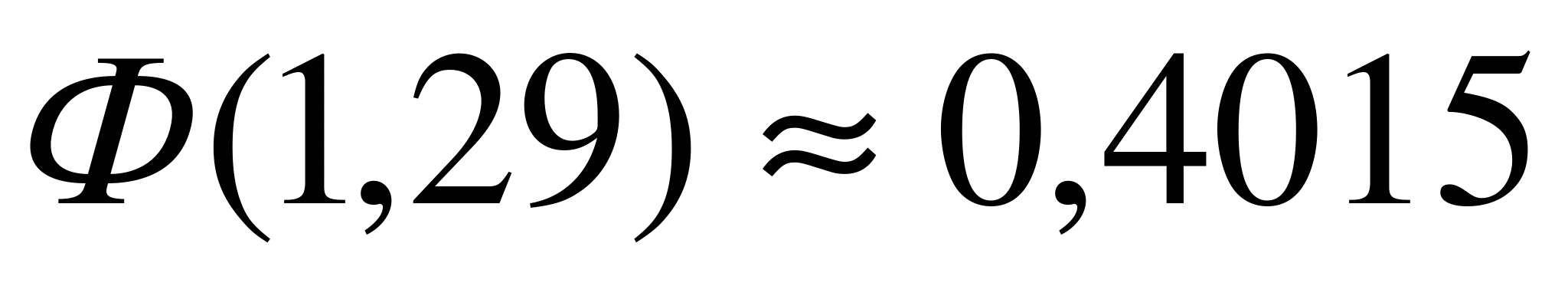Согласно условию задачи n =1000, p =0,6, q =1- p =0,4, e=0,02. Значит, = . По таблицам находим , и согласно формуле (6.5), .

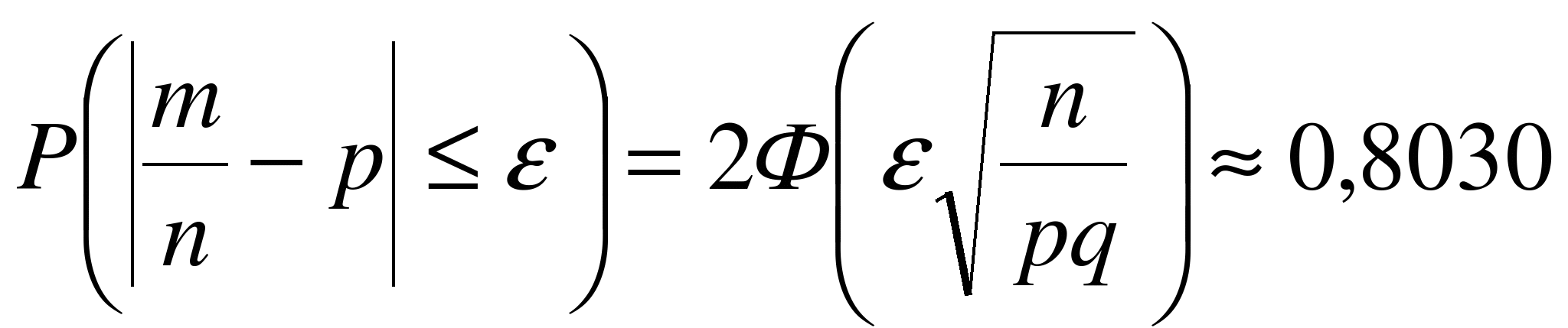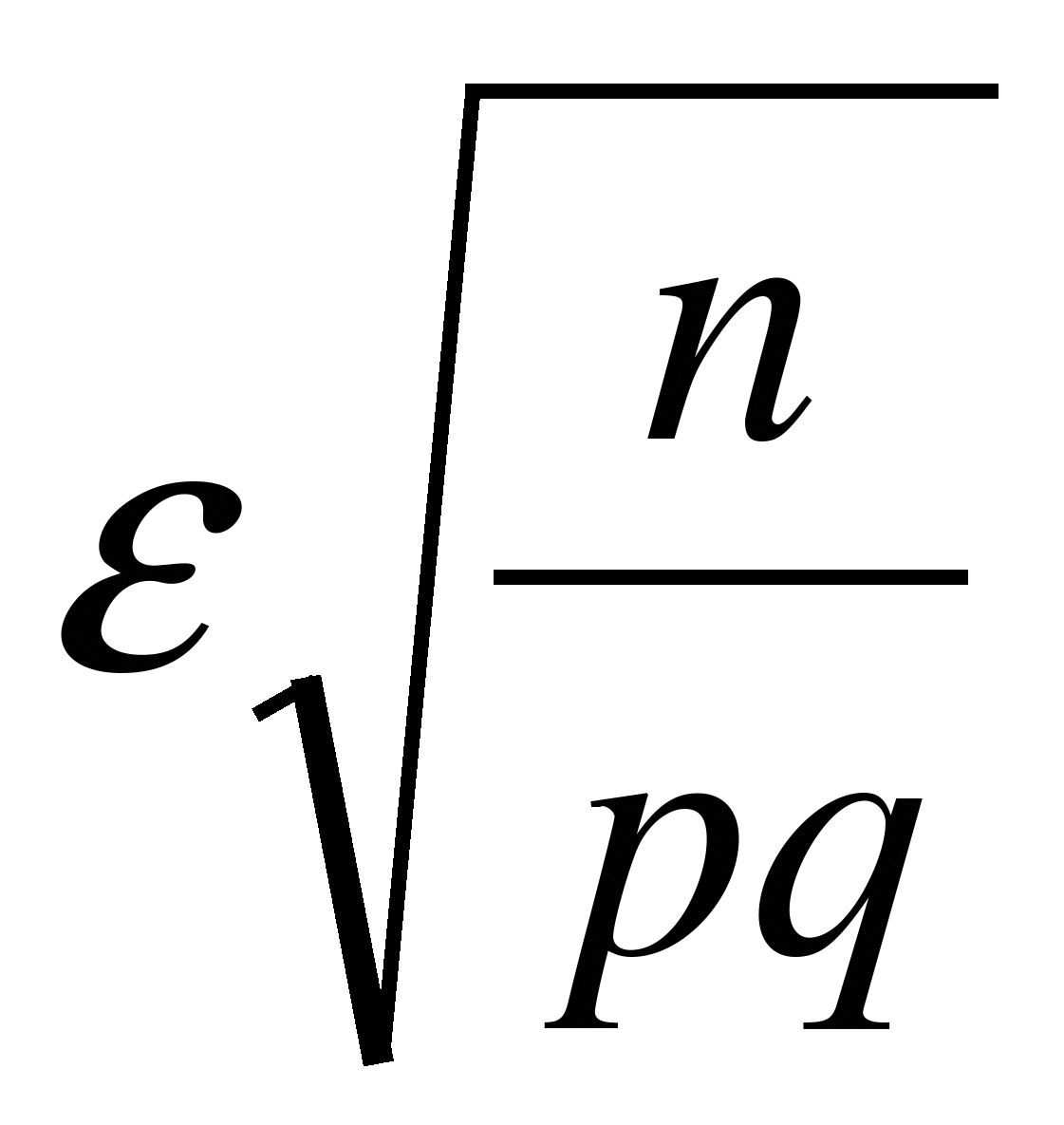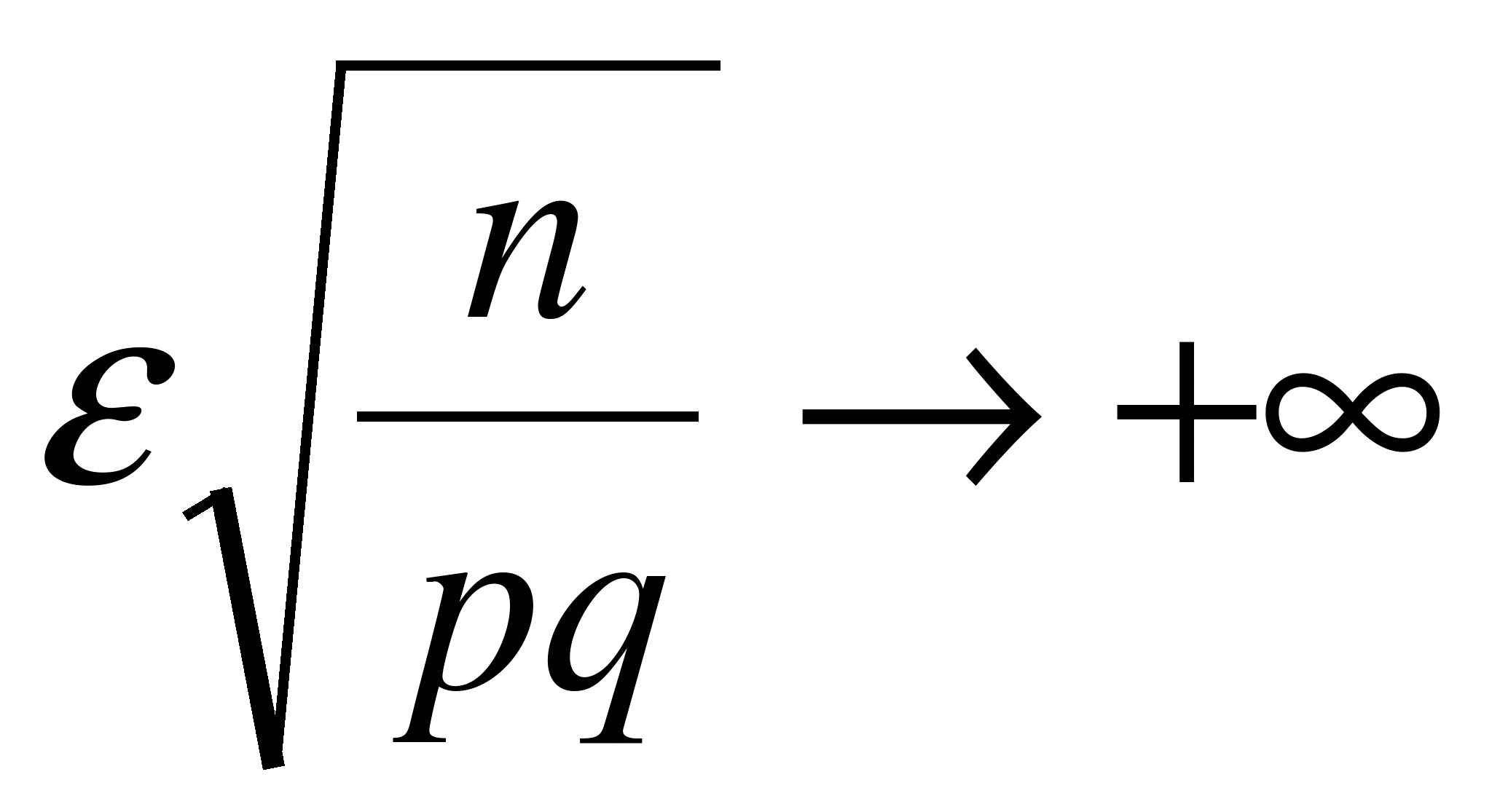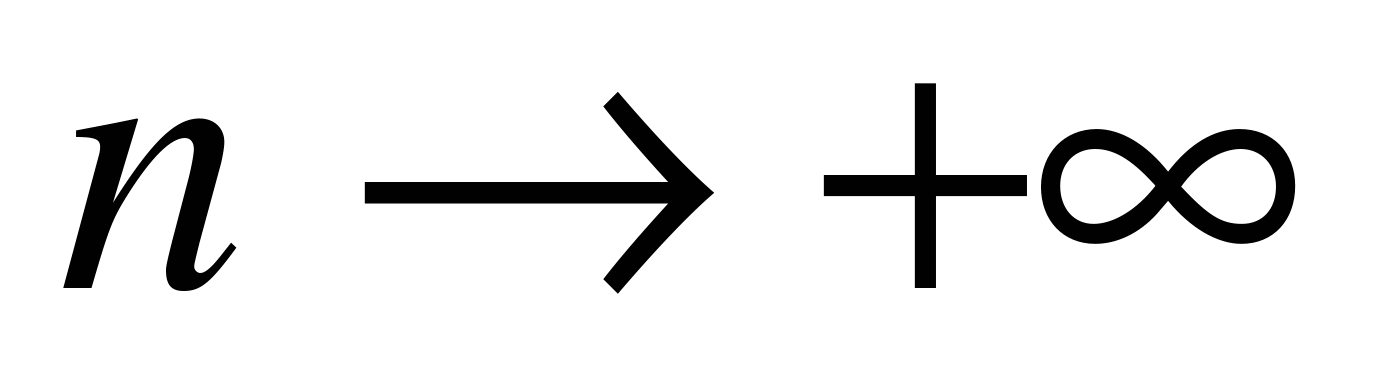Заметим, что при достаточно большом числе испытаний n и фиксированном e величина тоже велика ( при ), и 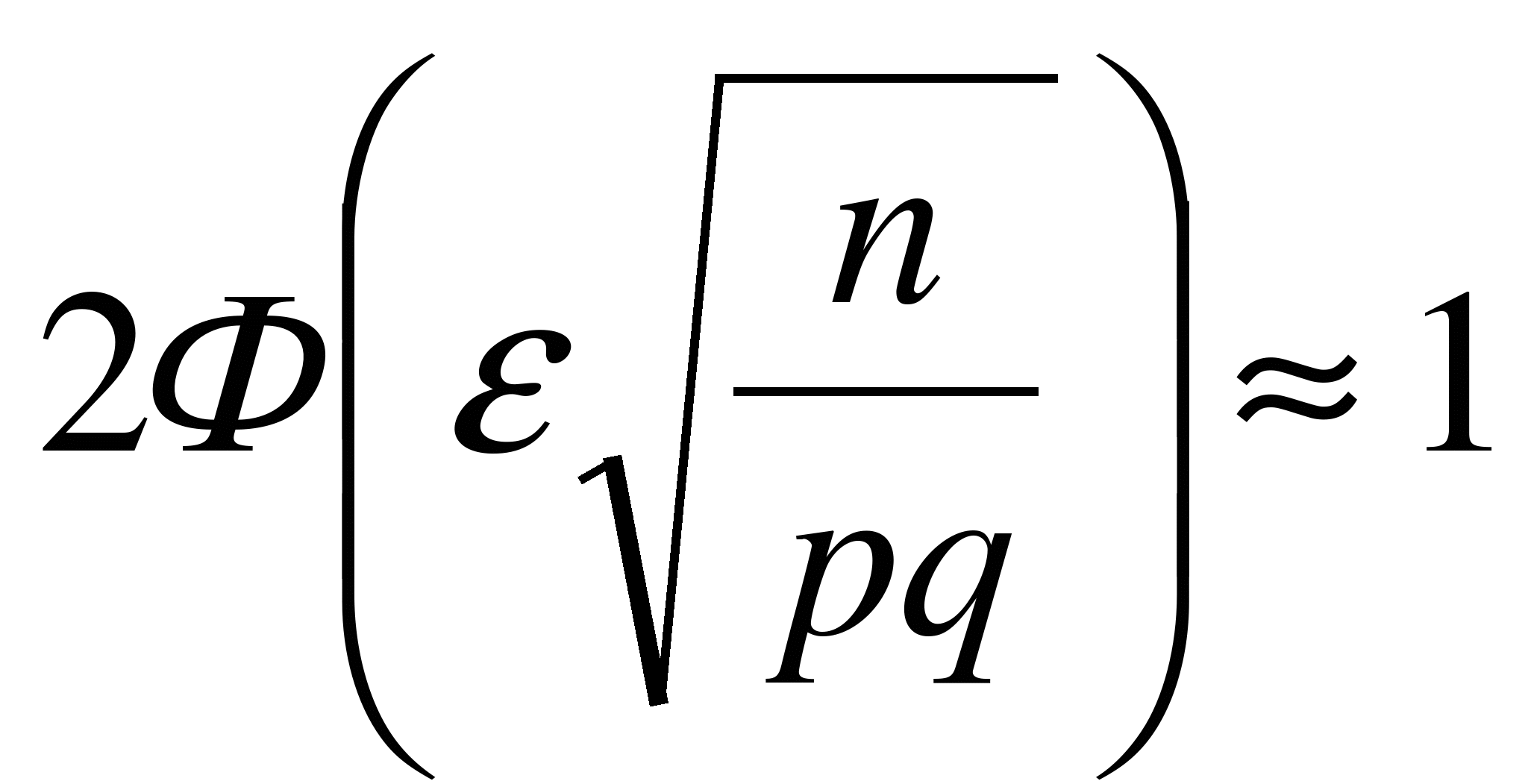(поскольку при x > 5 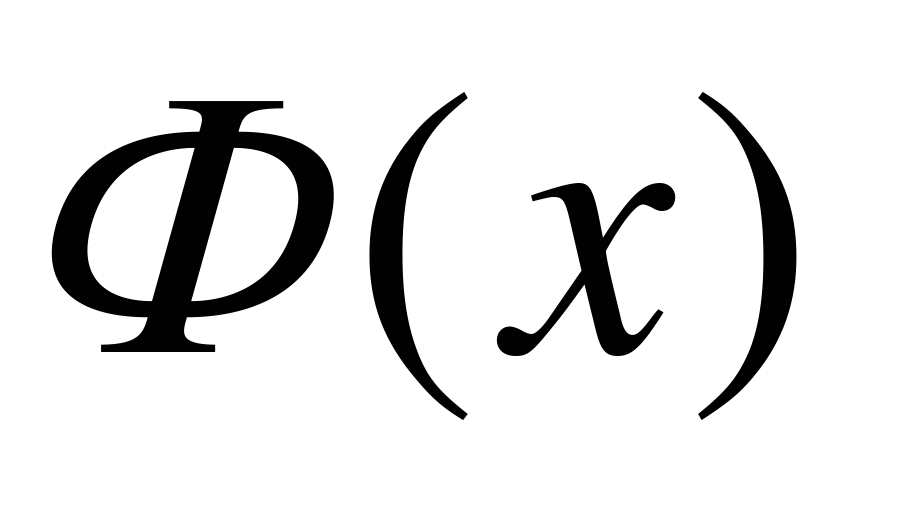»0,5). Это означает, согласно (6.5), что

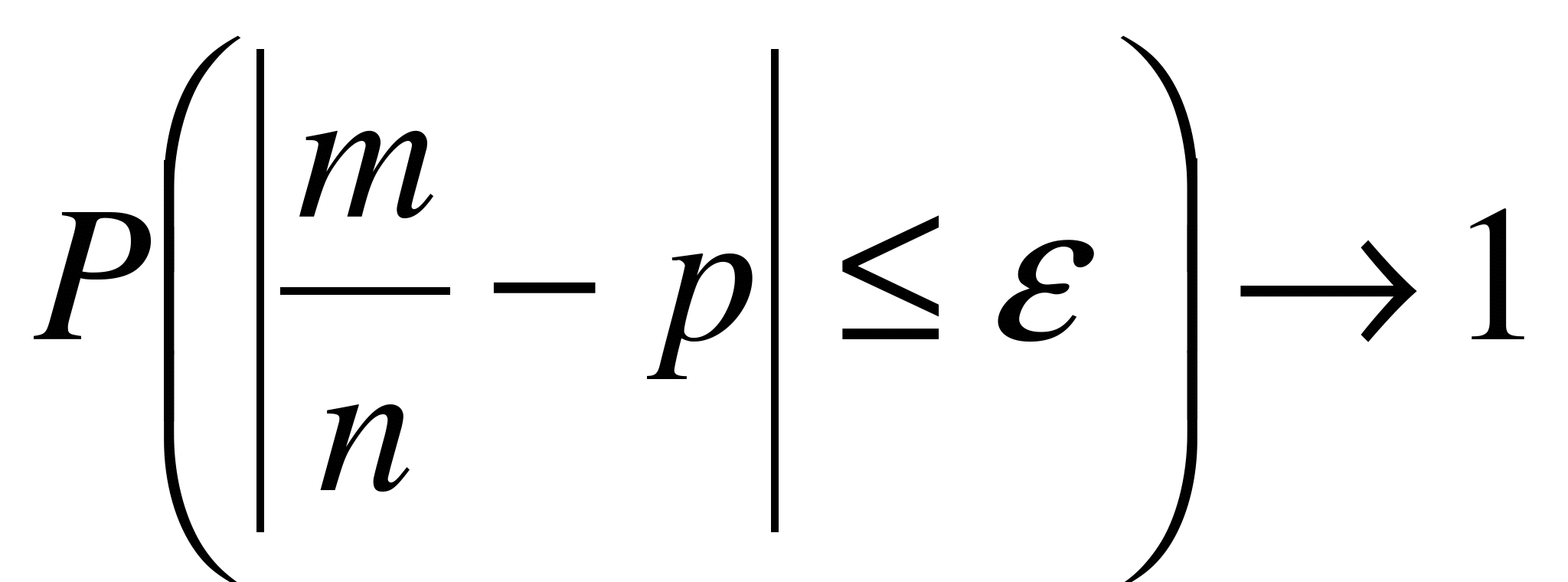при 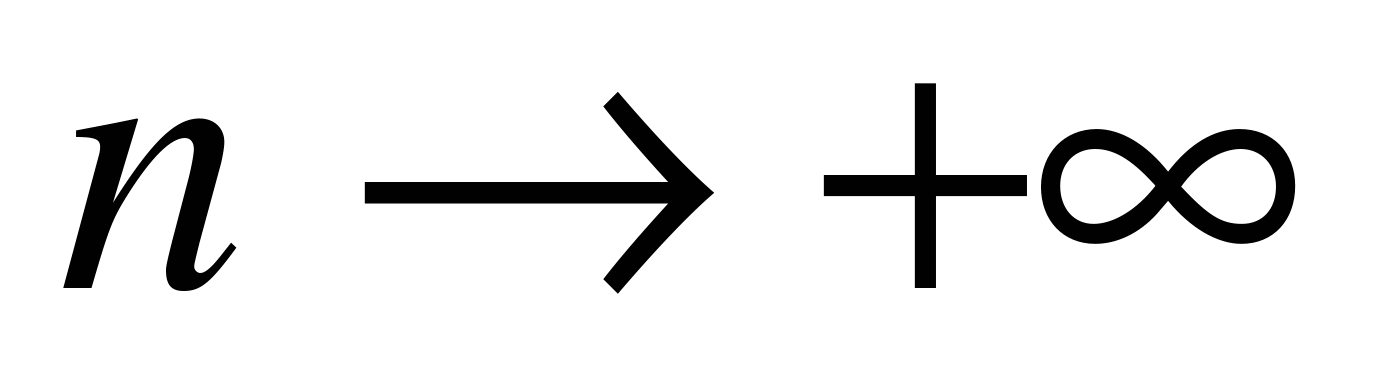. (6.6)

Соотношение (6.6) носит название теоремы Бернулли. Оно показывает, что при достаточно большом числе испытаний n практически достоверным можно считать тот факт, что отклонение относительной частоты m/n (т.е. статистической вероятности) наступления события А от его вероятности p не превышает по абсолютной величине любого сколь угодно малого заданного числа e.

Практически равенство (6.6) означает следующее: при большом числе испытаний n статистическая вероятность события m/n приближается к его классической вероятности p, т.е. 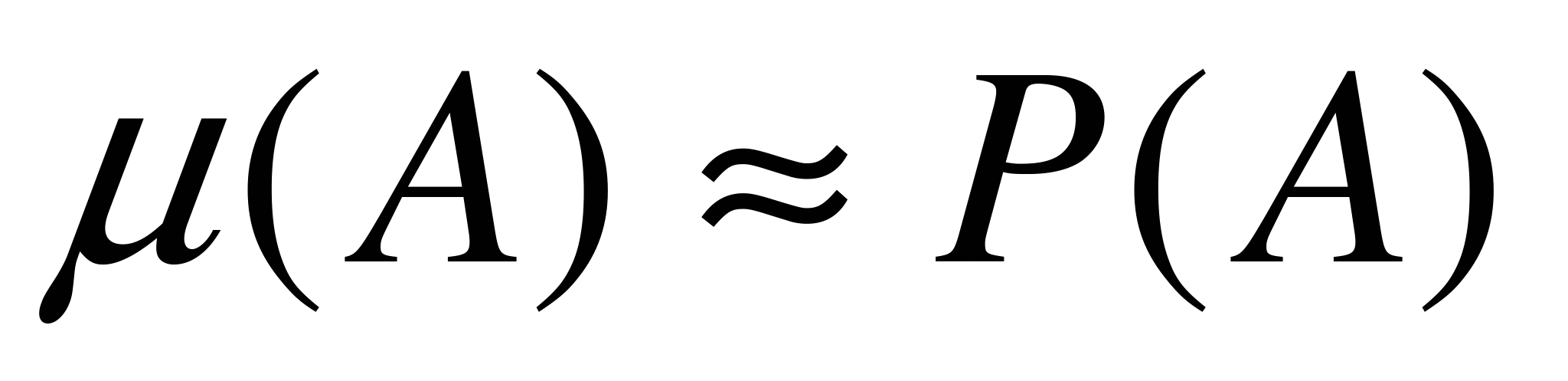. Подбрасывая монету достаточно большое число раз, мы вправе ожидать, что герб будет выпадать примерно в половине случаев. Бросая кубик достаточно большое число раз, можно ожидать, что шестерка выпадет в 1/6 части опытов и т.д.

В заключение параграфа приведем еще одну приближенную формулу для вычисления вероятности.

Если в условиях схемы Бернулли n достаточно велико, а 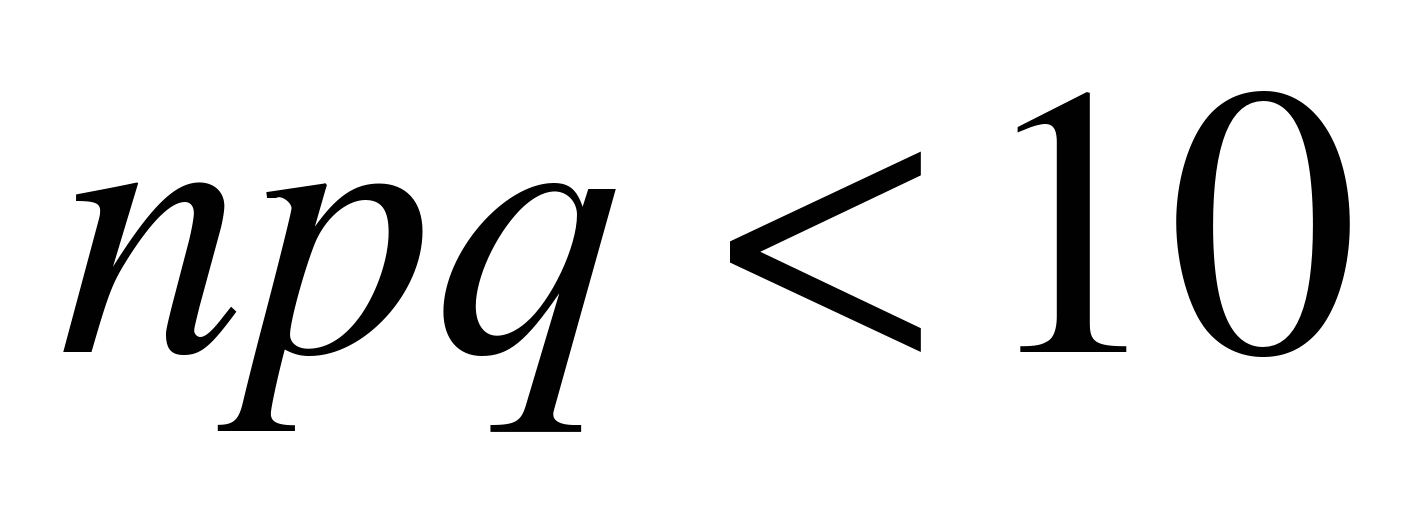, т.е. p близко к 0 или к 1, то теоремы Муавра – Лапласа уже не дают достаточной точности.

В случае, когда n велико, а p близко к 0 (т.е. событие А происходит редко), рекомендуется пользоваться приближенной формулой, полученной Пуассоном. Теорему Пуассона часто называют «формулой редких событий». Она дает хорошее приближение, если .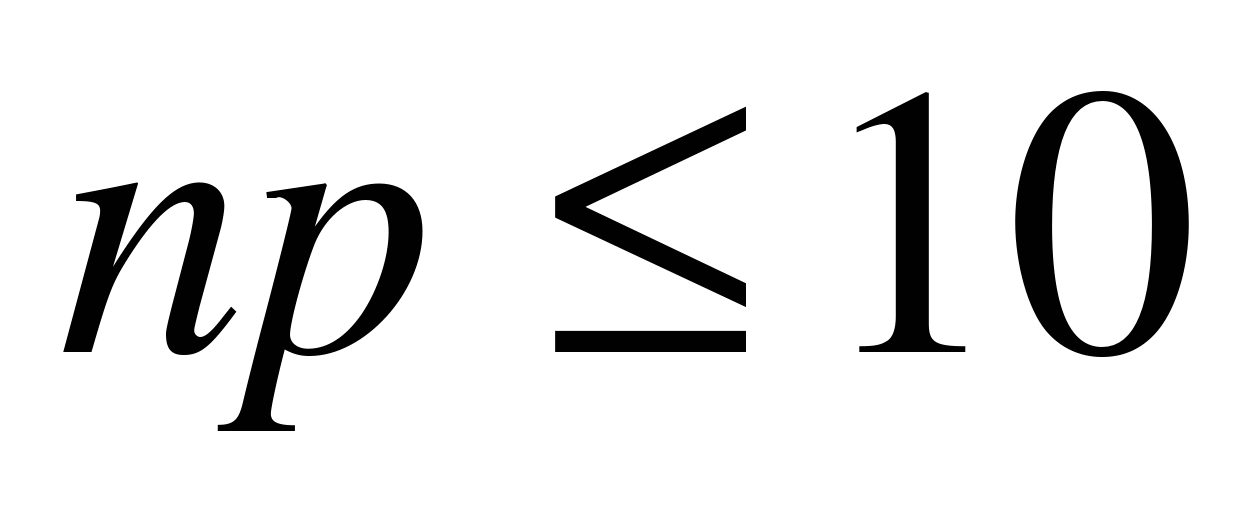

Теорема Пуассона.

Вусловиях схемы Бернулли, т.е. при проведении n независимых испытаний с двумя исходами, в каждом из которых вероятность появления события А постоянна и равна p (0 < p < 1), а вероятность появления противоположного события ` А равна q = 1 – p, для 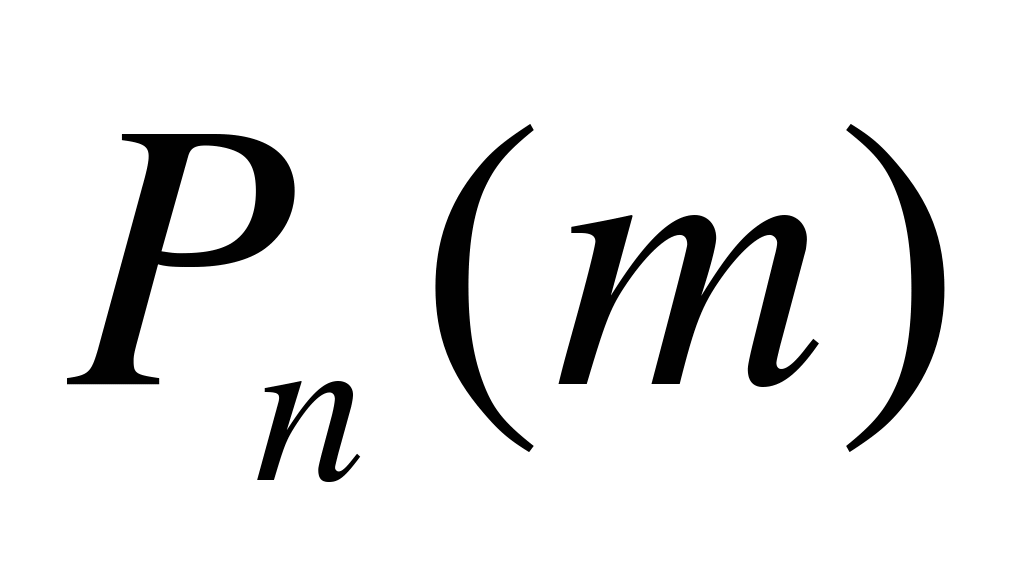(вероятности того, что в этих испытаниях событие А наступит ровно m раз) имеет место приближенное равенство

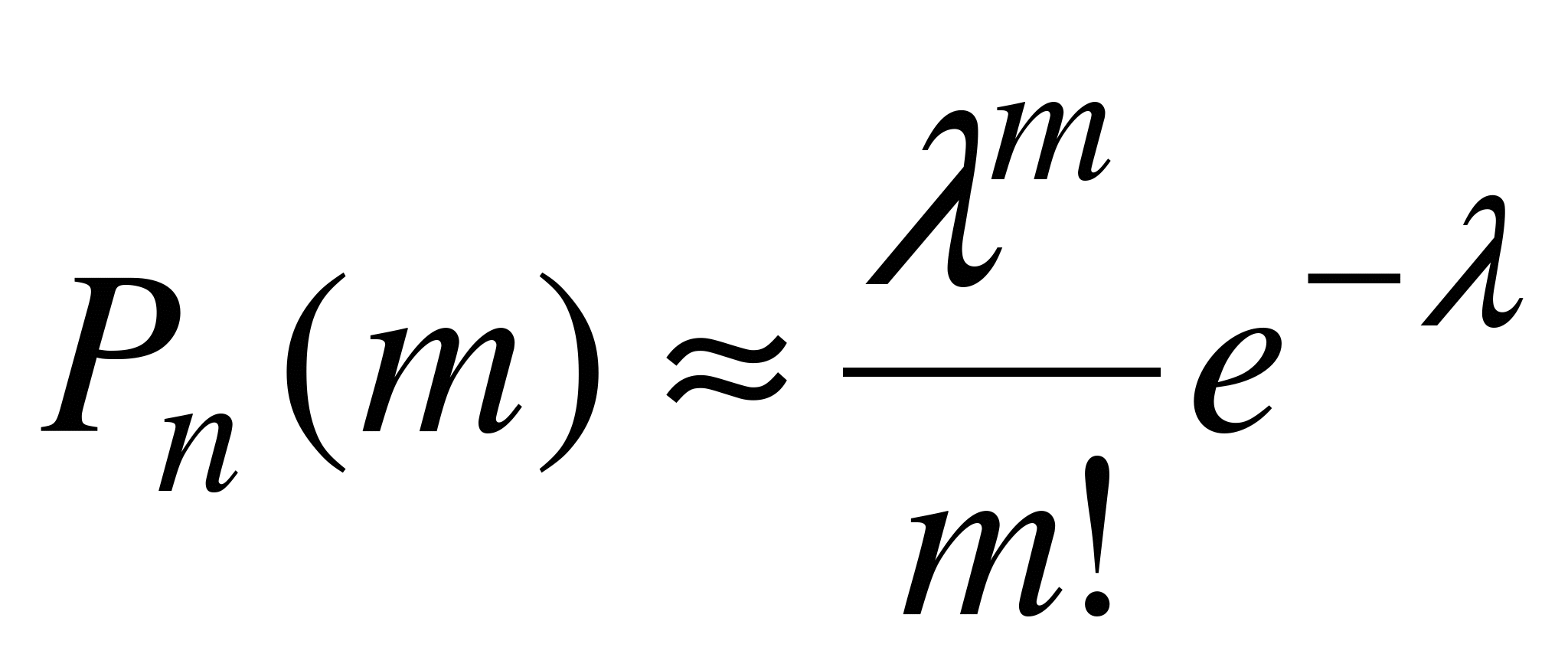, (6.7)

где .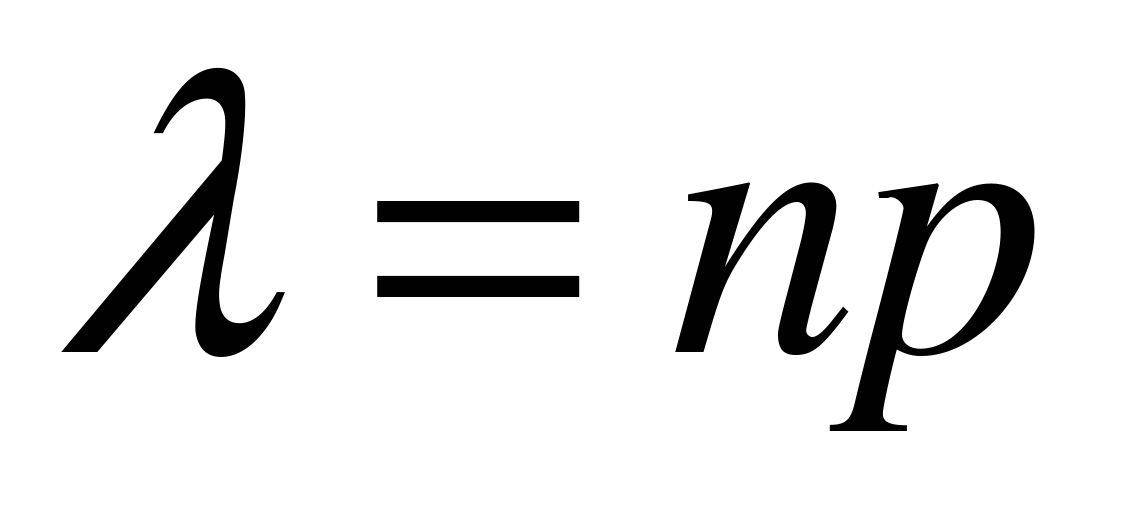

Пример 6.8. Известно, что в партии, состоящей из 5000 деталей, вероятность брака равна 0,0004. Вычислим вероятности следующих событий: а) в партии ровно 3 бракованных детали; б) бракованных деталей в партии не более трех; в) бракованных деталей больше трех.

а). Ясно, что мы находимся в условиях схемы Бернулли, причем 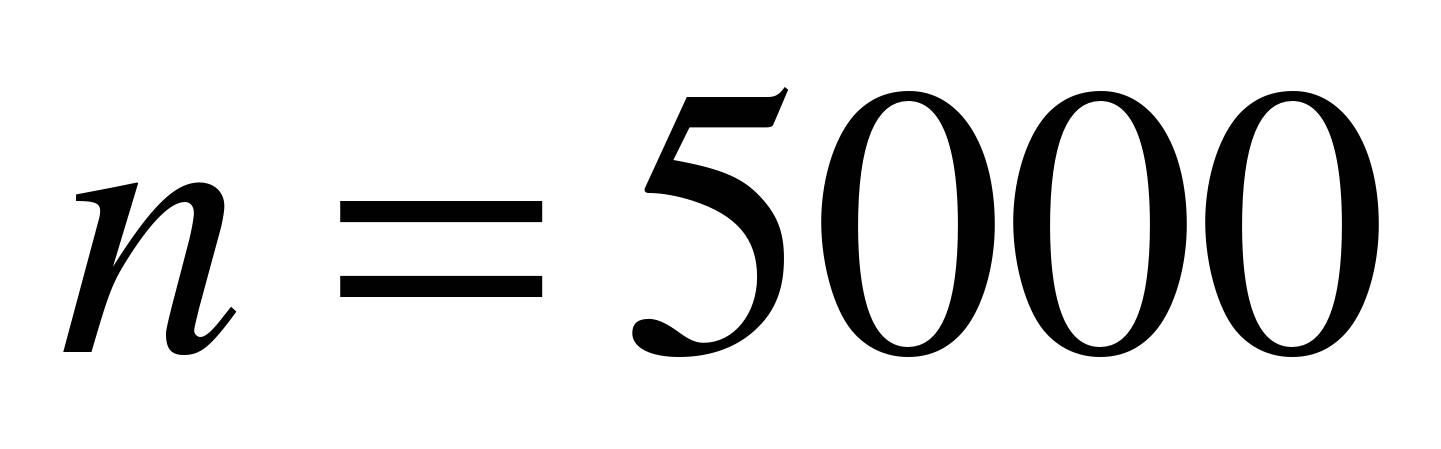, , 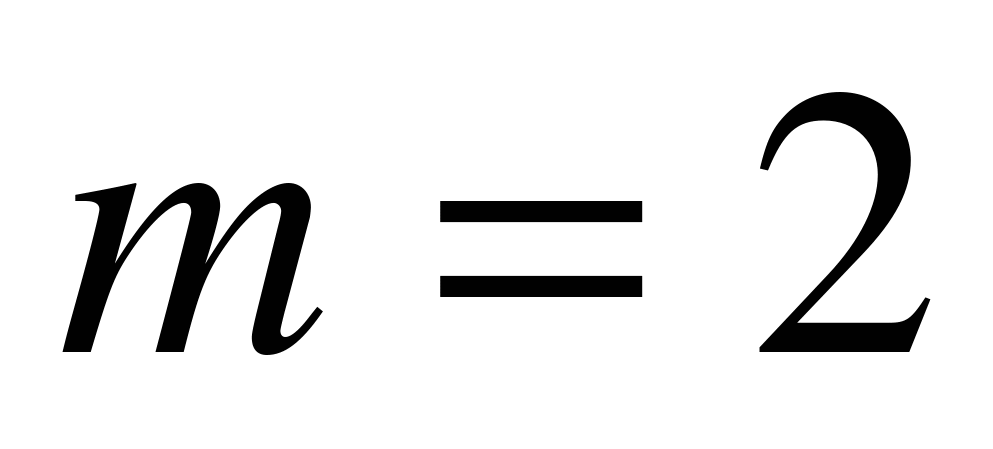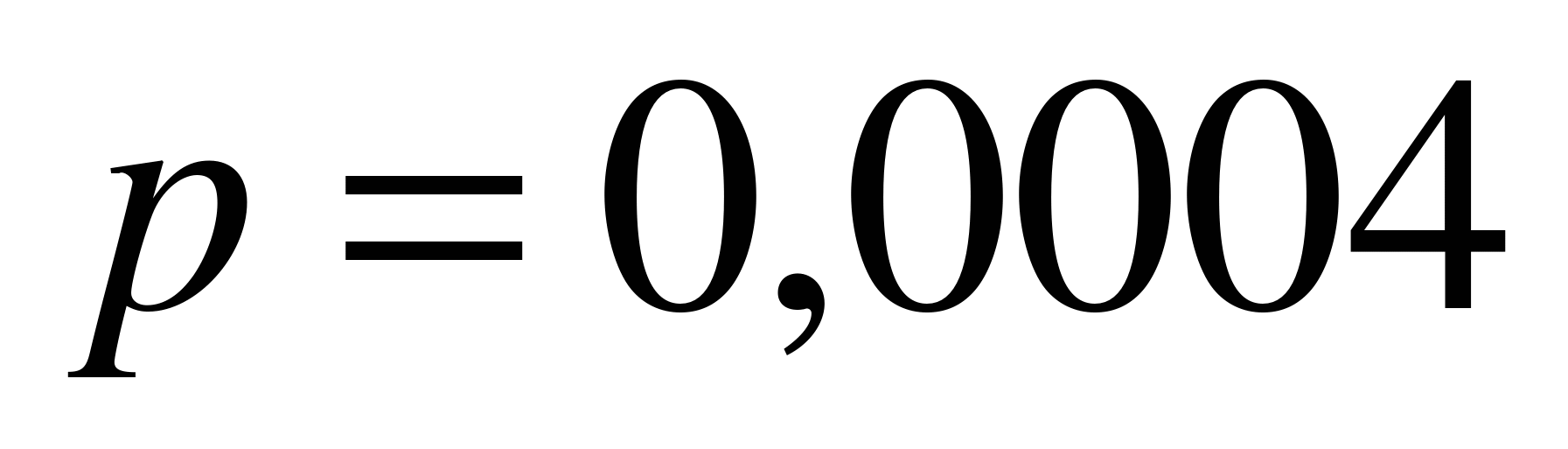. Поскольку n достаточно велико, а p близко к 0, 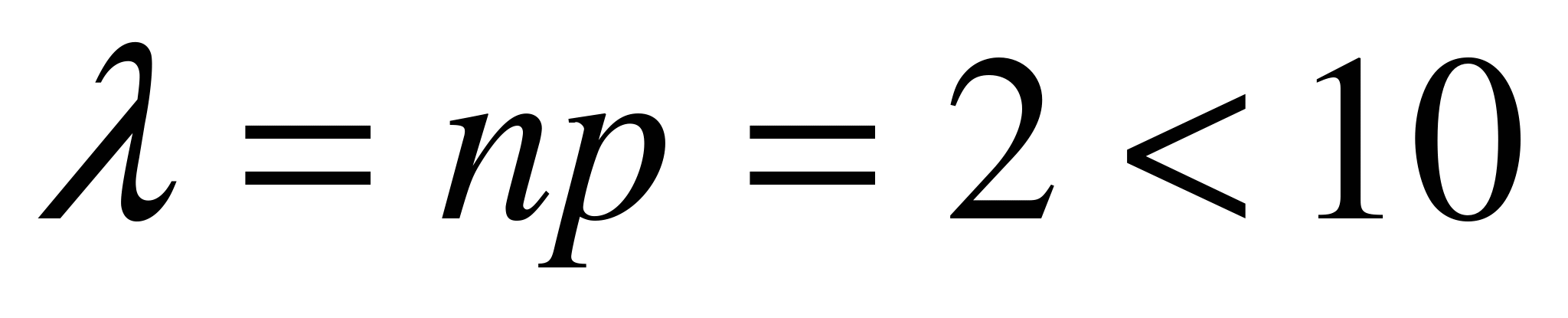, то для вычисления искомой вероятности нужно воспользоваться формулой (6.7).

.

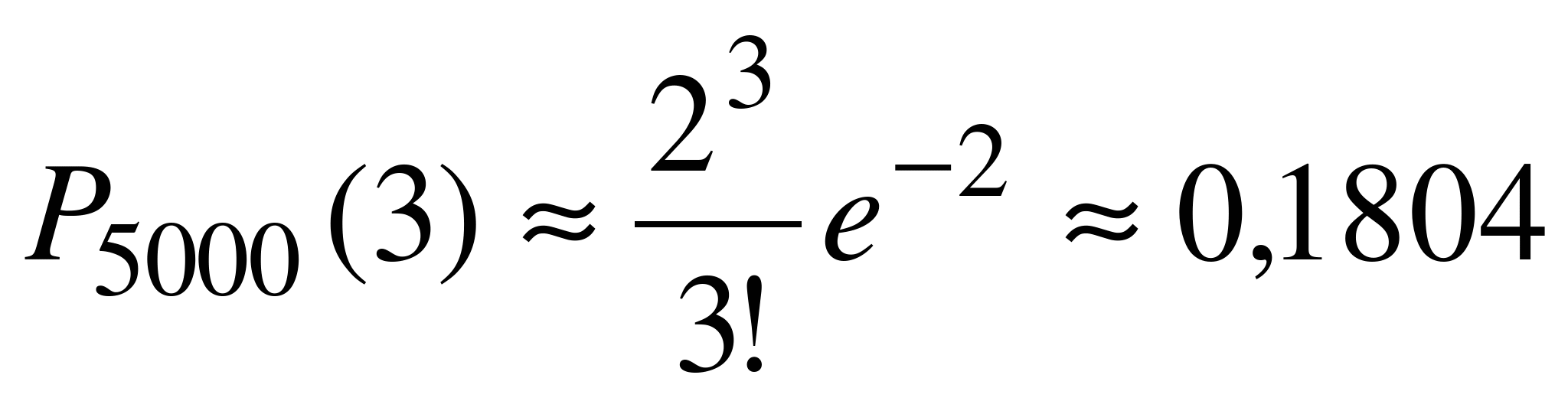б). Бракованных деталей в партии не более трех, если их 0 или 1 или 2 или 3, следовательно,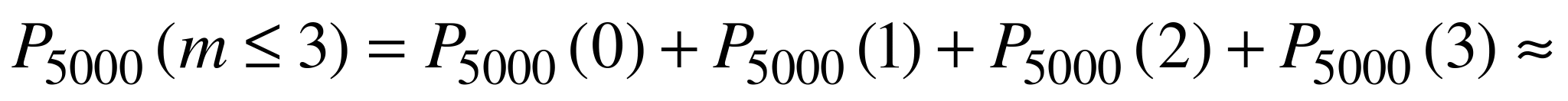

.

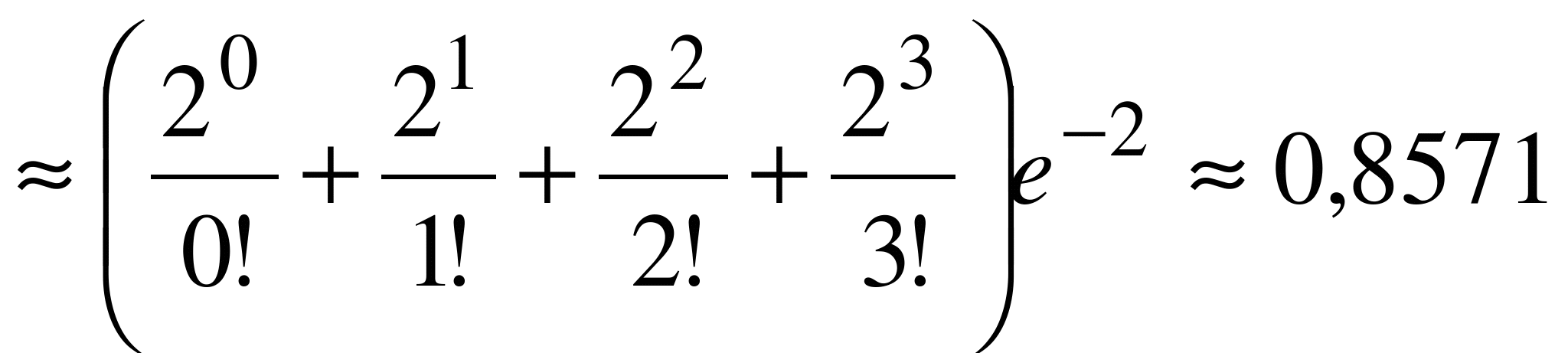в). Заметим, что события б) и в) в данной задаче противоположны, поэтому

.

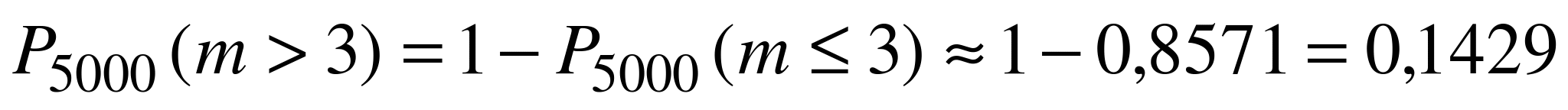Замечание. Если в условиях схемы Бернулли n достаточно велико, а p близко к 1, то q = 1 – p близко к 0, и теорему Пуассона можно применять к событию ` А (именно это событие будет происходить редко).