Их амплитудно-частотных характеристик по Тейлору

При аппроксимации амплитудно-частотной характеристики фильтра нижних частот по Тейлору требуется, чтобы при Ω = 0 функция (20.61) была равна единице, а все ее 2п —1 первых про­изводных были равны нулю. Этим требованиям удовлетворяет функция [47]

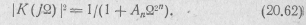
Такую функцию обычно называют максимально плоской или максимально гладкой.

На границе полосы пропускания фильтра (Ω=1) аппроксимирующая функция принимает вид

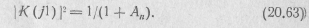
Обычно принимают A _n =1. При этом |K(jl) |²=0,5; | К(j1)| 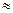0,707, а аппроксимирующая функция (20.62) будет иметь вид.

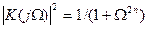. (20.64)

Для определения передаточной функции фильтра 'К(р) по ап­проксимирующей функции |K(jΩ) |² произведем замену jΩ = p. При этом получим

Приравняв нулю знаменатель этой функции, получим урав­нение

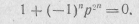
Корни этого уравнения

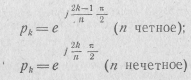
являются полюсами функции К²(р). Они располагаются на окруж­ности с единичным радиусом на равных расстояниях друг от друга. Всего получается 2п корней. Половина из них, находящаяся в ле­вой полуплоскости р, относится к К(р), а остальные — к К( —p ). При этом искомая передаточная функция фильтра будет иметь вид

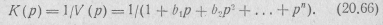
Полиномы знаменателя этого выражения получили название полиномов Баттерворта. Вычислять эти полиномы всякий раз, когда применяется аппроксимация по Тейлору, нет необходимости. Они приводятся в таблицах [47].

Полиномы Баттеоворта младших степеней имеют вид:

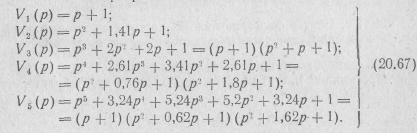
Степень п полинома Баттерворта определяют исходя из усло­вий задачи на расчет фильтра, а при определении величин эле­ментов фильтра учитывают нагрузку на его зажимах. Порядок расчета фильтра нижних частот с аппроксимацией его амплитудно-частотной характеристики по Тейлору рассмотрим на конкретном примере.

Пример 20.12.

Рассчитать нормированный фильтр нижних частот с аппроксимацией его амплитудно-частотной характеристики по Тейлору, если фильтр включен между

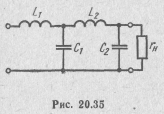
идеальным источником э. д. с. и активным сопротивлением r_H, нормированное значение которого равно единице. Значение амплитудно-частотной характери­стики фильтра на нормированных частотах Ω 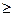2 должно быть не больше 0,1, а на границе полосы пропускания должно быть равно 0,707.

Решение.

Для определения степени п полинома Баттерворта воспользуемся выражением (20.64). Используя условия задачи из этого выражения, получим

,

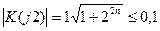откуда найдем 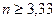. Поэтому выбираем n =4.

Подставив в формулу (20.66) полином Баттерворта четвертой степени (20.67), получим выражение для операторной передаточной функции фильтра

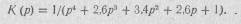
Для реализации этой функции воспользуемся методикой реализации реак­тивных четырехполюсников, изложенной в нодразд. 20.8. Так как числитель по­лученного выражения является четным полиномом, то, разделив четную часть знаменателя К(р) на его нечетную часть, найдем параметр Y₂₂ синтезируемого четырехполюсника:

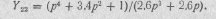
Разложив эту функцию в цепную дробь

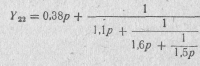
получим реактивный четырехполюсник, схема которого приведена на рис. 20.35. Нормированные значения его элементов:

C₂ = 0,38; L₂ = 1,1; C₁ = 1,6; L₁ = 1.5; r_H = 1.