Целочисленная задача ЛП

Когда часть переменных задачи ЛП или все переменные должны удовлетворять условию целочисленности, мы имеем дело с задачей целочисленного линейного программирования (ЦЛП), решить которую симплекс-методом уже не представляется возможным. В настоящее время большое распространение получили два метода решения задач ЦЛП: а) метод отсечений (алгоритмы Гомори); б) метод ветвей и границ (ВИГ). В данном разделе мы рассмотрим лишь второй метод решения, ввиду его простоты и удобства в структуризации процесса поиска оптимального решения.

Итак, рассмотрим метод ветвей и границ применительно к задаче

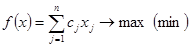. (8.1)

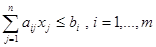
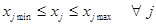
x_j – целые, j = 1,…,k; k ≤ n

Суть метода ВИГ заключается в том, что оптимальное решение исходной задачи будет удовлетворять одному из условий: либо 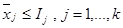, либо 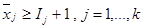, где I_j любое целое число между предельными значениями переменных x_{j min} и x_{j max}. Удобно, однако, в качестве величины I_j выбрать ближайшее целочисленное значение переменной, по значению которой происходит ветвление. Эта идея изображена на рис. 1. Исходная задача решается как обычная задача ЛП, без соблюдения условия целочисленности. Если полученное при этом решение оказывается целочисленным, то задача решена. В противном случае осуществляется «ветвление» множества допустимых решений по одной из нецелочисленных переменных.

Иллюстрируем применение метода ВИГ в решении следующей задаче

.

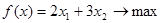5x₁+7x₂ ≤ 35

4x₁+9x₂ ≤ 36

x₁, x₂ ≥ 0, – целые

Решая эту задачу симплекс-методом, находим ее «обычное» решение в виде

.

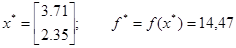Как видно, обе координаты не являются целочисленными. Выберем для ветвления одну из них, например, вторую координату, и составим две новые задачи: в задаче 2 к исходным ограничениям добавим ограничение х₂ £ 2, а в задаче 3 - ограничение х₂ ³ 3. Дальнейший ход алгоритма в виде дерева решений показан на рис. 2.

Когда найдено новое целочисленное решение, значение целевой функции этого решения сравнивается с верхним значением 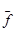(или нижним значением 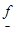при минимизации). В начале работы алгоритма это значение принимается равным 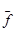= - ¥ ( 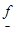= + ¥). Если значение целевой функции хуже предыдущего ее значения, то оно отбрасывается, а если лучше, то принимается за новое граничное значение, и т.д. В конце концов, нецелочисленные переменные примут целочисленные значения, если они существуют. Результаты решения задачи следующие: решение задачи 4: x^* = (4, 2)^T, f^* = 14 = 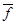; решение задач 8: x^* = (5, 1)^T, f^*=13; решение задачи 10: x^* = (7, 0)^T, f^* = 14 = .

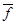Рис.2.4. К иллюстрации процесса

ветвления по координате х₂.

1.9. Задачи и вопросы для практических работ

Задача 1. Производственная программа фирмы представлена в виде задачи 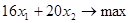при ограничениях , ; , .

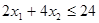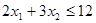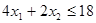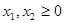а) Построить каноническую форму задачи;

б) построить область допустимых решений и линии уровня целевой функции.

в) найти графическое решение задачи и обосновать его оптимальность

г) оценить в отдельности влияние на оптимальное решение задачи коэффициентов целевой функции, технологических параметров и величин ресурсов.

Задача 2. Оптимизируемый объект описывается с помощью задачи

,

,

,

.

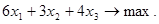
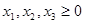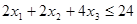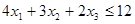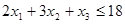а) Построить каноническую форму задачи;

б) найти все тройки линейно зависимых векторов матрицы расширенной задачи;

в) построить всевозможные базисы расширенной задачи, вычислить базисные решения и построить соответствующие вершины расширенного пространства решений

г) решить задачу с помощью табличного симплекс-метода, выделив все промежуточные базисы, базисные решения, текущие варианты.

д) оценить выбор максимальной симплекс – разности на ход алгоритма.

Задача 3. Построить двойственную задачу оптимизируемого объекта, описанного в задаче 2 и найти ответы на следующие вопросы:

а) в каком виде присутствует решение двойственной задачи в последней (оптимальной) таблице прямой задачи?;

б) проверить равенство целевых функций прямой и двойственной задач;

в) проверить, выполняются ли условия дополняющей нежесткости Слейтера для прямой и двойственной задач?;

г) убедиться в том, что двойственные переменные связаны с последним оптимальным базисом прямой задачи соотношением 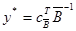или в эквивалентной форм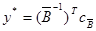е , где 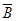- оптимальный базис, 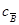- вектор коэффициентов при оптимальных базисных переменных.

Задача 4. Задача линейного программирования представлена в виде: максимизировать функцию 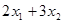при ограничениях , , .

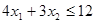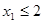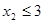а) Построить графическую картину задачи и найти ее решение;

б) построить расширенную задачу и найти всевозможные начальные базисы и базисные решения;

в) начиная с единичного базиса, иллюстрировать все этапы рекуррентной формулы 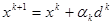и найти оптимальное решение задачи;

г) в координатной плоскости 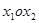показать проекции всех направлений движения, величин шагов, вершин расширенной области, в том числе и оптимальную вершину;

д) оценить вычислительную (или алгоритмическую) сложность табличного и рекуррентного алгоритмов симплекс-метода.

Ответ: .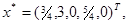

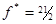Задача 5. Найти начальный базис задачи линейного программирования

(D, f): ,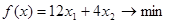

,

,

,

,

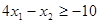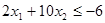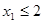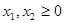используя метод искусственных переменных.

Задача 6. Найти все целочисленные решения задачи

,

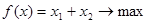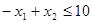
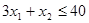
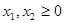, - целые

с помощью метода ветвей и границ. Построить и проанализировать соответствующее дерево решений и оценить альтернативные варианты ветвления.

Задача 7. Решить задачу целочисленного линейного программирования методом ветвей и границ

(D, f): ,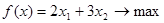

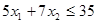
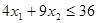
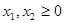, - целые

Построить всевозможные деревья решений и дать графическую иллюстрацию процесса ветвления.

Задача 8. Производственный план, отвечающий ограничениям 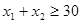, , 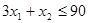, 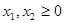должен максимизировать критерии 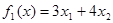, 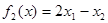. Исследовать этот план, ответив на следующие вопросы:

а) графически найти локальные оптимальные решения данной задачи;

б) показать области допустимых решений и оценок, а также подмножества оптимальных по Парето решений 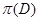и соответствующую эффективную границу ;

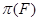в) задаваясь различными значениями коэффициентов важности 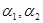, , 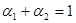найти графическим путем экстремум скалярной функции 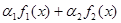и исследовать влияние 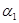и 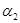на оптимальное решение;

г) выбрать одну из целевых функций в качестве главной и найти оптимальное решение при различных ограничениях для значений другой функции;

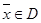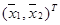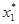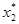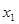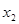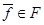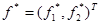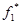д) графически найти точку , расположенную наиболее близко к точке где и наибольшие значения координат и . Как выглядит точка , которая находится на минимальном расстоянии от “утопической” точки , где и 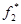- наибольшие значения критериев 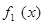и 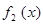на множестве D.

Задача 9. Проектируемый объект и критерий качества его функционирования представлены в виде модели оптимизируемой задачи

.

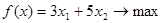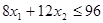
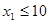
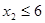
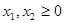
а) Применить метод множителей Лагранжа по отношению к этой и двойственной ей задачам и найти соответствующие условия теоремы Куна – Таккера;

б) графическим способом найти соответствующие оптимальные решения и проверить выполнение условий двойственности;

в) интерпретировать физический смысл переменных прямой и двойственной задач и убедиться в справедливости условий 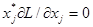, j = 1,2; 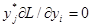, i = 1, 2, где L – соответствующая функция Лагранжа исходной задачи.