Задачи. 1. Построить примеры дизъюнкта Di = Р(х) Ú Q(y,f(z)) Ú R(u,g(x)), полученные в результате применения подстано-вок

1. Построить примеры дизъюнкта D_i = Р(х) Ú Q(y,f(z)) Ú R(u,g(x)), полученные в результате применения подстано-вок:

а) q = {а/х, b/z, f(a)/u}; б) l = {у/х, z/y}; в) s = {g(а)/х, g(z)/y, a/z}.

2. Найти композицию подстановок:

а) q = {c/х, f(z)/y, y/z} и l = {b/х, z/y, g(x)/z};

б) q = {a/х, z/y} и l = {y/х, b/z, g(a)/z};

в) q = {y/х, z/y, b/z} и l = {a/х, x/y, f(c)/z}.

3. Построить пример коммутативных подстановок. Доказать некоммутативность подстановок в общем случае.

4. Выяснить унифицируемость множеств. В случае положи-тельного ответа - определить наиболее общий унификатор:

а) {P(x), P(a), P(b)}; б) {P(x), P(y), P(b)}; в) {Q(x,y), Q(x,b), Q(z,y)}; г) {Q(a,b), Q(x,y), Q(x,c)}; д) {Q(x,y), Q(x,f(a,b)), Q(a,z)}.

5. Проверить наличие склеек у дизъюнктов и построить их:

а) P(х,a)Ú P(y,b)Ú Q(z); б) P(х)Ú P(a)Ú Q(y,f(x))Ú Q(y,f(a)); в) P(х) Ú Q(f(a))Ú P(f(a)); г) Q(х,y)Ú Q(y,f(a))Ú Q(z,u).

6.5.3. Правило и метод резолюции в теориях первого порядка

Определение. Рассмотрим дизъюнкты D₁ и D₂, назы-ваемые посылками. D₁ и D₂ не должны иметь общих пере-менных. Под дизъюнктом D^¢₁ будем понимать D₁ либо его склейку D₁s, под D^¢₂ - либо D₂ либо его склейку D₂s. Если литеры L₁ Î D₁ и Ø L₂ Î D₂ имеют наибольший общий унификатор s^¢, то дизъюнкт D = (D^¢₁ \ L₁s^¢) Ú (D^¢₂ \ ØL₂s^¢) называется резольвентой или заключением посылок D₁ и D₂. Литеры L₁ и L₂ называются отрезаемыми.

Понятия резолютивного вывода и доказательства не-выполнимости множества дизъюнктов путём вывода из него пустого дизъюнкта такие же, как и для ИВ.

Метод резолюций так же, как и метод, основанный на теореме Эрбрана, полон, т.е. его применение к невыполни-мому множеству дизъюнктов теоретически всегда приводит к резолютивному выводу пустого дизъюнкта ÿ. Однако в процессе построения резолютивного вывода также возмож-ны ситуации, когда он будет длиться недопустимо долго.

Для практического выяснения невыполнимости мно-жества дизъюнктов S необходимо путём применения ме-тода резолюции порождать все возможные дизъюнкты и присоединять их к S до тех пор, пока не будет получен пустой дизъюнкт. Для порождения резольвент можно ис-пользовать разные процедуры. Самым простым из них явля-ется метод насыщения. Его можно представить следующим образом.

ШАГ 0. Заданное множество S, а также все его склейки принимаем в качестве S₀.

ШАГ 1. В качестве множества S₁ принимаем все резольвен-ты, полученные из дизъюнктов S₀, а также их склейки.

ШАГ 2. В качестве множества S₂ принимаем все резольвен-ты, полученные из дизъюнктов D₁ Î (S₀ È S₁) и дизъюнк-тов D₂ Î S₁, а также их склейки.

...

ШАГ k. В качестве множества S_k принимаем все резоль-венты, полученные из дизъюнктов D₁ Î (S₀ È S₁È... È S_{k -1} ) и дизъюнктов D₂ Î S_{k -1}, а также их склейки.

Процесс порождения заканчивается после появления пустого дизъюнкта.

Анализ процесса резолютивного вывода показывает, что наряду с необходимыми порождается много лишних, избыточных дизъюнктов, которые не участвуют в выводе

пустого дизъюнкта. Всё множество избыточных дизъюнк-тов можно выявить только в конце доказательства. Однако часть из них можно выявить непосредственно в процессе вывода и сразу удалить из порождаемого множества. Таки-ми дизъюнктами являются, в частности, тавтологии (тож-дественно истинные дизъюнкты). Их вычеркивание не влия-ет на невыполнимость исходного множества S. Также можно вычеркнуть те из дизъюнктов, к которым частично или полностью могут быть сведены другие дизъюнкты.

Определение. Рассмотрим дизъюнкты D₁ , D₂. D₁ яв-ляется поддизъюнктом D₂ (поглощает D₂), если существует подстановка q, при которой D₁q Í D₂. D₂ называется над-дизъюнктом D₁. Частным случаем поддизъюнктов и над-дизъюнктов являются равные дизъюнкты (D₁ = D₂).

Правила, по которым производится удаление дизъ-юнктов, называются стратегией вычёркивания. В процес-се порождения дизъюнктов вычёркиваются все тавтологии и наддизъюнкты.

Проверка тавтологичности дизъюнкта сводится к про-верке наличия в нем контрарных пар литер (одинаковых, но отличающихся наличием отрицания).

Проверка поглощения дизъюнктов сложнее, так как само определение свойства дано через некоторую подста-новку, существование которой для сложных дизъюнктов неочевидно. Для дизъюнктов сложного вида применяют специальный алгоритм проверки поглощения.

Стратегия вычёркивания сохраняет полноту метода резолюции при значительном сокращении объёма необхо-димых выкладок.

Наряду с рассмотренной применяется ещё целый ряд разновидностей и модификаций метода резолюции, назна-чение которых - ускорить вывод пустого дизъюнкта в слу-чае невыполнимости исходного множества дизъюнктов.

ЗАКЛЮЧЕНИЕ К РАЗДЕЛУ “МАТЕМАТИЧЕСКАЯ ЛОГИКА”

Рассмотренные в разделе логики построены на буле-вых алгебрах. Классификацию их можно построить по двум основным признакам.

1. Мощность множества значений истинности k. Все логики можно разделить на:

а) алгебру логики (k=2),

б) многозначные логики (2 < k < À₀ ),

в) счётнозначные логики (½k½ =À₀ ),

г) континуальные логики (½k½= С).

½k½=À₀. Счётнозначные логики могут быть получены пу-тем обобщения многозначных при k®¥. В итоге получается логика со счетной мощностью (À₀) значений истинности. Обозначается такая логика Р_À0 . Множеством значений ис-тинности в Р_À0 является расширенный (включающий 0) натуральный ряд N₀ = {0, 1,... }. Элементарные функции вводятся по аналогии с Р_k. Cущественной особенностью данных логик является теоретическая невозможность пол-ного задания функций табличным методом. Применяется аналитическое задание, а фрагменты таблиц используют только для иллюстрации свойств соответствующих функ-ций.

½k½=С. Из логик с множеством значений истинности мощ-ности континуум рассмотрена только одна – нечеткая логи-ка, у которой значения истинности k Î [0,1]. Другим из-вестным примером континуальной логики с таким же мно-жеством значений истинности является теория вероят-ности. Предметным для неё является множество событий, на котором введены невозможное и достоверное события, выполняющие роль нулевого и единичного элементов, а

также операции отрицания, сложения и умножения. Данные операции введены таким образом, что алгебра событий (множество событий с введенными на нем операциями) об-разует булеву алгебру, в которой выполняются все 13 ак-сиом булевой алгебры. Логическая функция, заданная на множестве булевой алгебры событий, называется вероят-ностью. В отличие от нечеткой логики, она задаёт степень правдоподобности, возможности наступления соответству-ющего события. Как видно из приведенного примера, функциональные свойства логики во многом определяются содержанием логической функции и набора элементарных функций, введенных на предметной области. Вариантов выбора этих функций существует бесконечное множество.

После того, как в логике указано предметное мно-жество, логическая и элементарные функции, вводятся кон-струкции, называемые формулами. В математической логи-ке вторым существенным классификационным признаком является сложность формул, допускаемых в логике.

2. Сложность формул.

Как показано в логике предикатов, при одном и том же числе истинностных значений введение кванторов и предикатов позволяет получить значительно более сложную логику, включающую в себя исходную (бескванторную) в качестве частного случая. По сложности формул логики можно разделить на:

а) элементарные - не использующие кванторов и предика-тов,

б) логики первого порядка - допускающие предикаты и кванторы по предметным переменным,

в) логики второго порядка, у которых кванторы допуска-ются и по функциональным переменным и т.д.

В виде схемы общая классификаций логик по двум вышеприведенным признакам представлена на Рис.3.27.

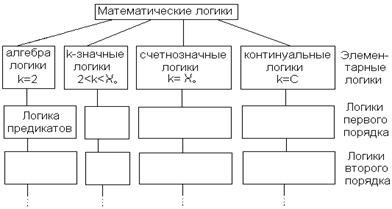
Рис.3.27

Как было показано, рассмотренные основные кон-структивные признаки только частично определяют каждую конкретную логику. Выработанные в математике приёмы позволяют строить логические теории, описывающие раз-личные явления на множествах объектов самой разной природы.

В науке основополагающая роль логики заключается в формализации знаний, в процессе которой систематизиру-ются соответствующие факты, явления и закономерности, выявляеся общность методов исследования в различных дисциплинах, границы применимости теорий и т.д.

Основное практическое значение формализации логи-ческих систем заключается в их последующей реализации при помощи различного рода вычислительных устройств, что позволяет создавать программные продукты и системы (например, робототехнические), обладающие элементами искусственного интеллекта. Применение логических мето-дов при расчете и проектировании сложных технических систем за счёт введения логических связей между объекта-ми позволяет намного упростить оперирование с ними, процессы композиции и декомпозиции.