The total work done in going around a complete cycle should be zero for gravity forces

To demonstrate this, we take a curve in a shape of square (Fig. 1). Then we calculate the work line-integral (2.6) from point 1 to 2, 2 - 3, 3 – 4, and 4 – 1.

; ; ; .

,

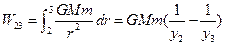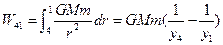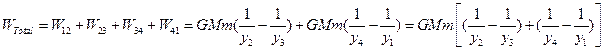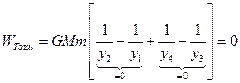, because 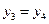and .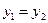

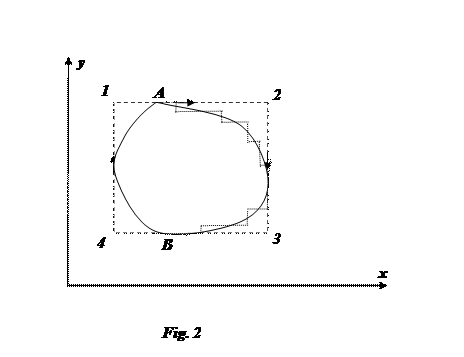
Of course we may wonder whether this is too trivial a curve. What if we use a real curve? Let us try it on a real curve. First of all, we might like to assert that a real curve could always be imitated sufficiently well by a series of vertical and horizontal lines Fig. 2.

All horizontal line-integrals give 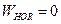, and the vertical integrals BA and AB equal .

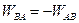So, .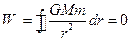

Now, we have the following two propositions: 1) that the work done by a force is equal to the change in kinetic energy of the particle, and 2) for a conservative force, the work done is minus the change in a function U which we call the potential energy.

As a consequence of these two, we arrive at the proposition that if only conservative forces act, the kinetic energy E plus the potential energy U remains constant:

(2.8) .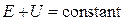

(2.9) .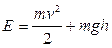

Race1

Now we have an interesting problem. Can we make perpetual motion in a gravitational field?

Can we design the curve so that it comes back moving a little bit faster than it did before, so that it goes around and around and around, and gives us perpetual motion?

We ought to discover the following proposition: since there is no friction the object should come back with neither higher nor lower velocity— it should be able to keep going around and around any closed path.

The total work done in going around a complete cycle should be zero for gravity forces, so the Perpetual Motion Machine has failed.