Метод искусственного базиса

Сформулированный выше алгоритм Симплекс-метода можно применять лишь в том случае, если выделено первое допустимое решение, т.е. исходная задача линейного программирования приведена к виду

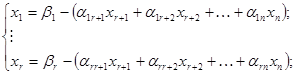
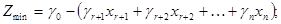
При этом 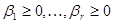, тогда, положив свободные неизвестные 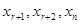равными нулю, получаем опорное решение .

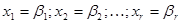Рассмотрю метод нахождения опорного решения, основанный на введении искусственных переменных. Для этого запишем задачу линейного программирования в общем виде. Будем рассматривать задачу с числом неизвестных 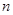и 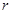ограничениями:

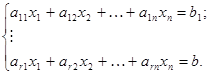(5.1)

Перепишем систему (5.1) в другом виде. Для этого введём искусственные переменные 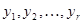так, чтобы был выделен базис. Тогда система примет вид

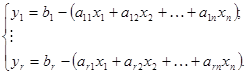(5.2)

Системы (5.1) и (5.2) будут эквивалентны в том случае, если все 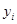, для 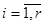будут равны 0. Кроме того, считаю, что все 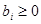для 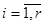. В противном случае соответствующие ограничения из системы (5.1) умножим на – 1. Для того чтобы 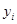были равны 0, мы должны преобразовать задачу таким образом, чтобы все искусственные переменные 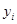перешли в свободные неизвестные.

В этом случае система (5.2) после преобразования примет вид:

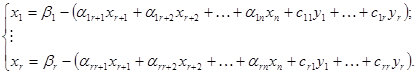(5.3)

От системы (5.2) к системе (5.3) всегда можно перейти шагами симплекс-метода. При таком переходе в качестве линейной формы рассматривают функцию

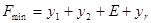, (5.4)

равную сумме искусственных переменных. Переход заканчивают, когда 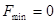и все искусственные переменные 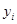переведены в свободные неизвестные.

Анализ вариантов решений

1. Если 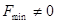, а все 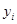переведены в свободные переменные, то задача не имеет положительного решения.

2. Если 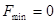, а часть 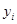осталась в базисе, то для перевода их в свободные необходимо применять специальные приёмы.

В симплекс-таблице, соответствующей системе (5.3), после того как 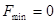, а все 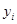- свободные, вычёркивают строку для 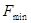и столбцы для 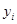и решают задачу для исходной линейной формы .

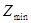Рекомендуется вводить минимум искусственных переменных.

5.2. Второй алгоритм отыскания опорного плана.

Пусть задача линейного программирования записана в каноническом виде:

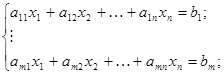(5.5)

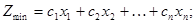(5.6)

, , , .

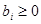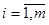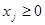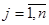Построим первую таблицу Жордана-Гаусса для задач (5.5) и (5.6). Для единообразия вычислительной процедуры к исходной таблице приписываем строку целевой функции:

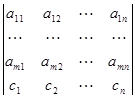
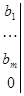
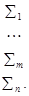(5.7)

После приведения системы ограничений к единичному базису целевая функция, как и базисные переменные, будет выражена через свободные переменные. Аналогичным приёмом я пользовался, когда решали задачи графическим методом с числом переменных более двух.