Потенциальная энергия. Потенциал поля

9.1. Понятие потенциальной энергии.

Определение: стационарное силовое поле, в котором работа силы поля на пути между любыми двумя точками не зависит от выбора пути, а зависит только от положения этих точек, называется потенциальным полем (силы - консервативными).

Можно иначе: если работа сил на замкнутом пути равна нулю, то поле потенциально.

Для потенциального поля можно ввести понятие потенциальной энергии, исходя из следующих обстоятельств:

1. в системе, где действуют только консервативные силы, всякая работа связана лишь с изменением конфигурации системы (взаимного расположения тел);

2. работа сил равна нулю, если система возвращается к исходной конфигурации.

Определение: запас работы, определяемый начальной конфигурацией тел системы, называется потенциальной энергией системы.

Пример: тело в поле силы тяжести и растянутая пружина обладают определенным запасом работы, которую они могут совершить.

Заметим, что запас работы можно отсчитывать от разных конфигураций.

Пример: для тела, поднятого на высоту 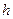от поверхности земли и на высоту 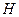от дна колодца, запас работы различен в зависимости от точки отсчета.

Т.о., телу всегда можно приписать любое наперед выбранное значение потенциальной энергии. Это соответствует тому обстоятельству, что путем измерения совершаемой работы может быть определена лишь разность потенциальных энергий различных конфигураций системы.

Выбор новой отсчетной конфигурации, просто заменяет одно нулевое положение другим, в свою очередь, изменяя потенциальную энергию любой конфигурации системы на одну и ту же постоянную величину. Следовательно, работа, определяемая как разность потенциальных энергий системы в двух различных конфигурациях, сохранит свое значение.

Покажем это, определив работу при переходе системы из положения 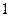в положение 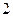через потенциальные энергии соответствующих конфигураций.

Пусть точка 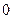характеризует положение системы, от которого производится отсчет потенциальной энергии .

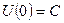По определению, потенциальная энергия равна

в точке 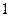: 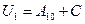, в точке : .

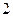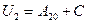Тогда для консервативных сил можно записать

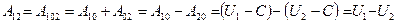. (9.1)

Работа, совершаемая консервативными силами при переходе системы из

положения 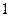в положение 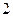, равна убыли потенциальной энергии системы.

Работа сил в потенциальном поле при переходе из точки 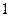в точку 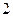не

зависит от выбора точки отсчета потенциальной энергии.

Т.о., потенциальная энергия системы определена с точностью до произвольной постоянной, зависящей от выбора, так называемой, нулевой конфигурацией системы, и в этом смысле всегда существует неоднозначность в её абсолютном значении.

Однако если ход физических явлений зависит лишь от разности значений потенциальной энергии системы в различных состояниях, то произвол в выборе начальной конфигурации (произвольной постоянной) не может отразиться на величине совершенной системой работы.

В отличие от кинетической энергии, которая существенно положительна, потенциальная энергия может быть меньше нуля. Так, например, потенциальная энергия взаимодействия двух одноименно заряженных частиц больше нуля (если на бесконечно большом удалении их друг от друга она положена равной нулю), а разноименно заряженных частиц – меньше нуля.

Отметим еще одно важное обстоятельство. Потенциальную энергию следует относить не к частице, а к системе, которая состоит из частицы и взаимодействующих с ней тел, создающих силовое поле. При заданном характере взаимодействия потенциальная энергия взаимодействия частицы с данными телами зависит только от положения частицы относительно этих тел.

9.2. Примеры потенциальных полей.

1) Однородное поле тяжести.

Потенциальная энергия тела массой 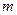в однородном поле тяжести равна

,

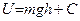тогда

.

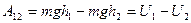Константу 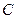можно условно положить равной 0 (отсчитывать, скажем, от уровня моря),

2) Поле упругих сил.

Потенциальная энергия растянутой (сжатой) пружины.

.

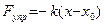Элементарная работа растяжения:

,

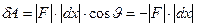где 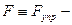сила, возникающая при деформации пружины.

Знак «минус» появился из-за того, что перемещение и сила направлены в

разные стороны.

Полная работа при возвращении пружины в недеформированное состояние равна

.

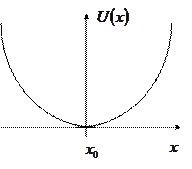
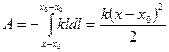Эта работа равна убыли потенциальной энергии пружины:

.

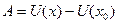Если энергию недеформированной пружины положить

равной нулю (в точке 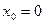), то потенциальная энергия упруго

деформированной пружины:

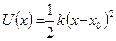, (9.2)

или иначе - потенциальная энергия осциллятора.

Осциллятор (от лат. оscillo – качаюсь) – физическая система, совершающая колебания.

3) Гравитационное поле.

Сила притяжения двух материальных точек массам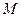и и 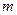: 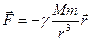- сила центральная, консервативная. Для простоты считаем, что масса покоится, а масса 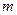притягивается к ней и перемещается. Сосчитаем работу по перемещению точки 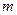из бесконечности в точку :

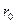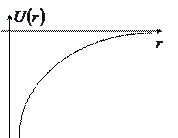
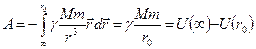
Будем отсчитывать потенциальную энергию, считая, что на бесконечности :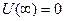

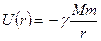. (9.3)

Из (9.3) следует, что запас гравитационной энергии (работы) максимален при бесконечном расстоянии между телами.

Отметим, что такие же соотношения (с точностью до знака) справедливы для кулоновского взаимодействия.

9.3. Связь между силой и потенциальной энергией (градиент).

Взаимодействие частицы с окружающими телами можно описать двумя способами: рассматривая силы взаимодействия или рассматривая потенциальную энергию взаимодействия.

Вообще говоря, первый способ описания обладает большей общностью, т.к. применим к таким силам, поле которых не является потенциальным (например, сила трения). Однако зачастую «энергетический» подход к решению поставленной задачи является гораздо более эффективным, значительно упрощая её решение.

Установим связь между потенциальной энергией и силой поля. Сформулируем задачу следующим образом: пусть имеется силовое поле, характеризуемое потенциальной энергией 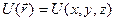как функцией положения частицы в поле; требуется найти силу 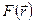по заданной потенциальной энергии. Работа консервативной силы на конечном пути определяется соотношением (9.1). По аналогии выразим и элементарную работу силы поля как убыль потенциальной энергии и, одновременно, как скалярное произведение силы на перемещение:

,

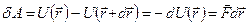или

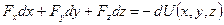. (9.4)

Запишем работу силы при малом перемещении вдоль оси :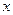

,

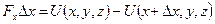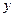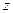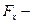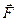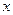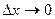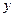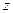предполагая, что значения координат и не изменяются; проекция вектора на ось . Тогда (переходя к пределу при и полагая и постоянными) выражаем 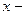компоненту силы 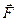через частную производную от функции :

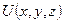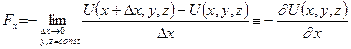. (9.5)

Замечание. Символ частной производной 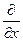означает, что функция 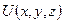при дифференцировании должна рассматриваться как функция одного аргумента 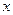, остальные же аргументы (в данном случае 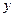и 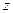) должны при этом оставаться постоянными.

Аналогичные соотношения получаем для двух других переменных.

Итак, проекции силы 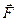на координатные оси:

.

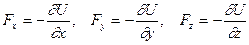Т.о., вектор силы 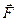равен

.

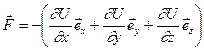Величину, стоящую в скобках, называют градиентом скалярной функции .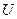

Символически полученное выражение можно записать следующим образом:

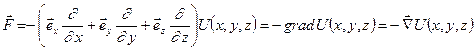. (9.6)

Мы ввели оператор градиента:

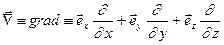. (9.7)

Формально операцию 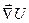можно рассматривать как произведение вектора 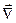на скаляр 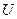, имея в виду, что скалярная функция 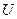должна стоять справа от векторного оператора .

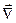Итак, мы установили связь между силой поля и потенциальной энергией как функцией координат. Теперь, зная потенциальную энергию частицы в поле, можно определить силу, действующую на частицу в каждой точке рассматриваемого пространства:

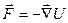, (9.8)

т.е. сила поля равна со знаком минус градиенту потенциальной энергии частицы в данной точке поля.

Примечание: в выражении (9.4) стоит полный дифференциал потенциальной энергии:

.

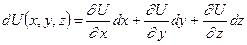Смысл оператора «градиент» (градиента).Эквипотенциальные поверхности.

Если ввести понятие эквипотенциальной поверхности – поверхности, во всех точках которой потенциальная энергия имеет одинаковое значение, то можно наглядно интерпретировать смысл термина (операции) «градиент».

На рисунке изображены эквипотенциальные кривые, причем 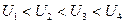, и показано направление векторов 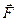и 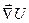в точке .

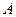Из формулы (9.6) следует

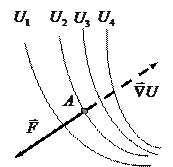1. проекция вектора 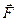на любое направление, касательное к

эквипотенциальной поверхности в данной точке, равна нулю.

Следовательно, вектор 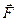нормален эквипотенциальной

поверхности в данной точке.

2. вектор 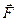направлен в сторону уменьшения 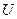и

противоположен по направлению вектору .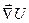

Т.о., получаем, что градиент 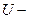это вектор, направленный

по нормали к эквипотенциальной поверхности в сторону

возрастания потенциальной энергии .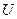

9.4. Поле и потенциал поля.

Опыт показывает, что для гравитационных и электростатических взаимодействий сила 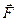, действующая на частицу со стороны окружающих тел, может быть представлена в виде произведения двух величин:

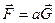, (9.9)

где 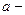скалярная величина, которую следует понимать как массу или заряд частицы, соответственно, 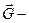векторная величина, зависящая как от положения частицы, так и от свойств окружающих тел.

Такой подход позволяет связать физическую интерпретацию взаимодействия с понятием поля. Говорят, что система окружающих частицу тел создает в пространстве поле, характеризуемое вектором 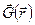. Частица, помещенная в это поле, испытывает на себе действие силы, определяемой выражением (9.9). При этом считают, что поле, задаваемое вектором 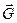, существует безотносительно к тому, находится в нем интересующая нас частица или нет. Вектор 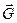называют напряженностью поля.

Принцип суперпозиции полей.

Одно из важнейших свойств поля заключается в том, что поле, образованное несколькими источниками, равно сумме полей, созданных каждым из них, т.е.

.

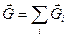Потенциал поля.

Используя введенные понятия и обозначения, можем записать

,

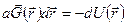поделив обе части уравнения на 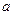и обозначив 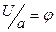, получаем

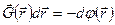, или .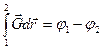

Функцию 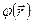называют потенциалом поля. Потенциал поля, как и потенциальная энергия, определяется с точностью до прибавления произвольной постоянной, которая является несущественной и поэтому обычно опускается.

Потенциалы гравитационного поля точечной массы 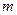и кулоновского поля точечного заряда 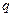определяются формулами

.

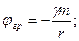
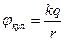Итак, поле можно описывать как векторным 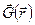, так и скалярным 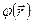способом. Оба способа адекватны. Практически скалярный способ описания поля в большинстве случаев значительно удобнее.

Связь напряженности и потенциала поля.

Зная функцию 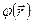, легко восстановить вектор поля :

,

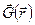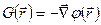что непосредственно следует из (9.8).

Пример: кулоновское поле.