Постановка задачи оптимизации. Оптимизация конструкции заключается в отыскании мума одного показателя качества или их совокупностей

Оптимизация конструкции заключается в отыскании мума одного показателя качества или их совокупностей. В первом случае оптимизацию называют скалярной, а во втором - векторной, Кроме того, в зависимости от характера исходных данных различают или детерминированный случай, или оптимизацию в условиях неопределенности.

Если условия задачи и ограничения заранее известны, то задача сводится к детерминированному случаю, а если часть условий неизвестна, то такую задачу оптимизации относят к случаю ее решения в условиях неопределенности,

Условиями задачи будем называть те исходные данные, которые заданы и мы изменять их не можем. Условиями могут быть показатели качества, параметры конструкции, воздействия и т. д. В процессе оптимизации, с учетом заданных условий, мы должны найти элементы решения, т. с. те параметры кона рукции и показатели качества, которые зависят от нашего выбора и которые приводят к отысканию оптимальных конструкций.

Обычно в задачах оптимизации ищется экстремум интеграль­ного показателя или целевой функции, которая в общем случае является функцией многих аргументов. Она задается в некото­рой области значений переменных. Наименьшее или наибольшее значение целевой функции из всех возможных в заданной об­ласти называют глобальным экстремумом. Если в заданной области существуют экстремумы, меньше глобального, то их называют локальными.

Экстремумы называют граничными, если они находятся на границах области задания целевой функции. В том случае, если область не ограничена, т. е. элементы решения x_i не имеют ог­раничений, то экстремумы называют безусловными.

При ограниченной области задания целевой функции экс­тремумы называют условными.

Если целевая функция зависит от n-переменных, то услови­ем существования экстремума является равенство нулю всех частных первых производных от целевой функции. Полученная экстремальная точка называется стационарной.

При этом математическая модель целевой функции известна или задана. Предположим, что обобщенным показателем каче­ства является эффективность К_эф.

Заданы исходные данные или условия α_i, на которые кон­структор опирается в процессе работы как на константы и из­менять их не может.

Требуется найти элементы решения x_i т. е. величины, зави­сящие от его выбора.

Условиями и элементами решения могут быть не только кон­станты, но и функции.

Предположим, что оптимизируется показатель качества K_эф:

К эф = К (α₁,…, α_n, x₁, …, x_i, …, x_m).

Задача оптимизации сводится к отысканию таких x_i, которые обращают K_эф в максимум.

Простейшим методом решения этой задачи, как отмечалось ранее, является отыскание экстремума путем взятия производных от K_эф по аргументам x_i. Приравнивая производные нулю, I чим систему уравнений, из которой можно найти ний x_i: ∂K_эф/∂x₁ = 0, …, ∂K_эф/∂x_m = 0.

Однако такая простая методика применяется для нахождения оптимальных решений в том случае, когда существуют экстремумы и производные, т.е. функция эффективности не имеет особенностей. В практических задачах часто экстре­мумы находятся па границе допустимых решении.

Для некоторых задач опти­мизации необходимо использо­вать векторную оптимизацию, т. е. находить оптимальное решение по нескольким показателям. Эта задача характерна для случая, когда показатели качества противоречивы, например надежность и стоимость, прочность и габаритно-массовый показатель и т. д.

Предположим, что отыскивается оптимальное решение в об­ласти двух конфликтующих параметров, например стоимости и надежности. Последовательно задаваясь элементами решений x_i находим наиболее приемлемые их значения. Допустим, что нам известна допустимая область изменения элементов стоимо­сти и надежности. Задаваясь дискретными значениями элемен­тов решения, найдем значения показателей стоимости С и на­дежности Р. Все полученные решения сведем в табл. 3.1. Пред­полагается, что известна функциональная зависимость между С и Р.

Таблица 3.1

Показатель качества	Элементы решения х решения х
x1...... xn
Значения С	C1...... Cn
Значения Р	P1...... Pn

Максимальные значения надежности и соответствующие ми­нимальные значения стоимости дают оптимальные решения.

Для большей наглядности изобразим полученные решения на графике (рис. 3.1) в координатах С и Р. Очерченная область заключает в себе желаемые решения.

Рис. 3.1. График, поясняющий нахож дение области оптимальны решений при противоречивых параметрах С и Р

Если оптимизация производится по n параметрам, то анало­гично предыдущему случаю строят таблицу и находят область (пространство) допустимых решений. При этом исключают те решения, которые выходят за рамки ограничений.

Математическая модель задачи оптимизации независимо от уровня оптимизируемого конструктивного модуля при детермини­рованном случае записывается в виде max К = φ (А, X); min К = φ (А, X), или

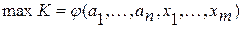
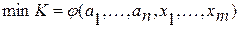
где К - оптимизируемая целевая функция; А - известные заданные условия; Х—элементы решения.

На условия и на элементы решения наложены ограничения

.

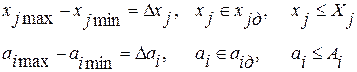где X_j, A_j - наложенные ограничения.

В зависимости от структуры оптимизируемой целвой функции могут использоваться различные методы оптимизации.

Если, например, целевая функция зависит линейно от условий и элементов решения, то с успехом используется ли­нейное программирование, если эта зависимость нелинейна, то методы нелинейного програм­мирования и т. д. Следователь­но, метод программирования определяется видом целевой функции и ограничений.

В дальнейшем в целях удоб­ства изложения иногда вместо показателей качества или целевых функций употребляем термин «критерий». Аргументом в пользу такого перехода служит то, что критериями могут быть и не обязательно показатели качества.

Рассмотрим некоторые возможности объединения показате-лей качества или критериев в один общий критерий К₀. Эту операцию называют приведением многокритериальной задачи к задаче скалярной оптимизации.

Простейшим методом объединения критериев является их суммирование с учетом весов W_i К₀ = ∑ W_iK_i, где n — количество объединяемых критериев; W_i — весовой коэффициент.

При объединении критериев подразумевается, что они приведены к единой шкале. Кроме того, должно выполняться условие K_i≥K_iд. Это условие налагается при невозможности «перекомпенсации» одних критериев за счет других.

Весовые коэффициенты определяются одним из методов, рас­смотренных в 1.3, а приведение к единой шкале осуществляет­ся путем выражения критериев в относительных значениях, т. е. их нормированием относительно допустимых значений K_iд.

С учетом изложенных замечаний оптимизируется зависимость вида

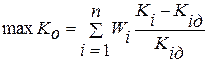
Вторым методом объединения критериев в один общий является представление их в виде произведения. Этот метод применяют в том случае, когда отдельные критерии безразмерны, например представлены в виде вероятностей.

При этом максимизируется функция

.

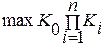Примером такого объединения критериев может служить оценка вероятности выполнения задачи.

При наличии противоречивых критериев, т.е. когда один из них необходимо максимизировать, а другие минимизировать, возможно использование критериев вида

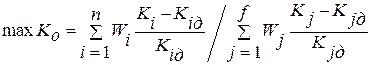
В данном случае i-е показатели максимизируются, а j-е ми­нимизируются.

Приведенные примеры формирования обобщенного критерия не ограничивают возможность представления К_о в другом виде. Здесь показаны наиболее общие принципы построения обобщен­ного критерия без учета физической сущности оптимизируемых объектов или процессов.