Представление о моментах случайных величин и их свойствах

Моменты - универсальные характеристики распределения слу­чайной величины, наиболее часто используемые в математической статистике. В терминах моментов можно описать основные характеристики рассеяния, см. выше § 3.2 и знакомство с ними необходимо для свободной ориентации в положениях классической теории, а также в отечественных и зарубежных статистических данных.

Моментом распределения (М_к) называется средняя арифмети­ческая из отклонений значений признака х_i от некоторой постоян­ной величины a в степени к. Порядок момента определяется величи­ной к. Эмпирический момент к - гопорядка определяется по формуле:

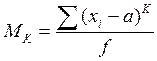
В зависимости от постоянной величины а различают началь­ные, центральные и условные моменты. В частности, если а равно среднему значе­нию признака х_i, то момент называется центральным.

Начальный момент первого порядкаслучайной величины X называют также математическим ожиданием (МО), или средним значе­нием 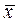(его обозначают через МX или ЕX).

Для дискретной случайной величины X со значе­ниями x₁, х₂,..., имеющими вероятности р₁, р₂… .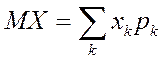

Для непрерывной случайной величины X с распределением вероятностей f_X (х) .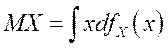

Свойства математического ожидания:

1. МО постоянной равно этой постоянной.

2. МО суммы случайных величин равно сум­ме их МО, т.е. .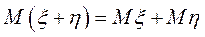

3. МО произведения случайной величины на константу равно произведению этой константы на МО случайной величины (иначе, постоянный множитель можно выносить за знак МО): .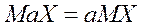

Второй центральный мо­мент (или центральный мо­ментвторого порядка) DX называется обычно дисперсией D, см. § 3.2, и используется для количественной оценки раз­броса случайной величины.

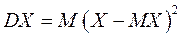или 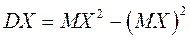(3.10)

Свойства второго центрального мо­мента илидисперсии:

1. Дисперсия постоянной величины равна нулю.

2. Для любой постоянной а:

, .

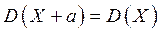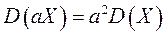Асимметрия (в программе EXCEL - "СКОС") и эксцесс - также центральные моменты, но соответственно 3-его и 4-ого порядка. Ещё одно их характерное отличие от ранее рассмотренных моментов - они не зависят от размерности случайной величины. Для этого их нормируют, деля на соответствующую степень стандартного отклонения:

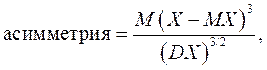(3.11)

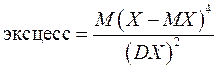(3.12)

Асимметрия (А) характеризует степень несимметричности распределения относительно среднего значения. Расчётная формула для выборки:

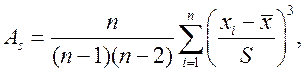(3.13)

где n – объем выборки;

x_i – i - ое значение выборки;

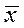и S – среднее значение и стандартное отклонение выборки.

Положительная (правосторонняя) асимметрия указывает на отклонение распределения в сторону положительных значений (вправо по числовой оси). Отрицательная (левосторонняя) асимметрия указывает на отклонение распределения в сторону отрицательных значений (рис.).

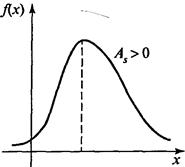
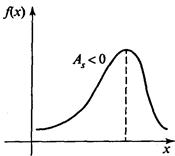
а б

Рис.. Правосторонняя (а) и левосторонняя асимметрии (6)

Эксцесс (обозначается Е или ε) характеризует степень выражен­ности «хвостов» распределения, т.е. частоту появления значений, удаленных от математического ожидания. Для нормального распределения эксцесс, определяемый по формуле (3.12), равен 3, а при расчёте по формуле для выборки (3.14) за счёт дополнительно введённого второго члена - нулю. (Таким же образом он рассчитывается в программе EXCEL, см. § 2.2). В результатеотносительно более «остроконечное», чем нормальное распределение имеет положительный эксцесс, а относительно более «сглаженное» - отрицательный эксцесс (рис 3.4).

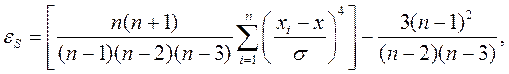(3.14)

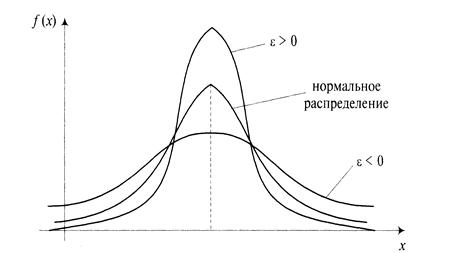
Рис. 3.4. Схематическое изображение распределения с положительным и отрицательным эксцессом