Методы решения задач нелинейного программирования

1. Геометрический. При использовании геометрической интерпретации решение производится по алгоритму:

1. По системе (1) находят область Ω

2. Строят гиперповерхности вида ƒ(x₁…x_n)=h, h – произвольный параметр

3. Находят гиперповерхности наивысшего (наинизшего) уровня для задачи максимизации (минимизации). Общие точки области Ω и этой гиперповерхности – решение задачи. Если гиперповерхность наивысшего (наинизшего) уровня найти невозможно, то целевая функция неограничена сверху (снизу), т.е. задача максимизации (минимизации) не имеет решения.

Пример:

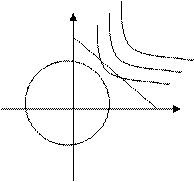ƒ=x₁*x₂→ max x₂

­­­

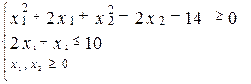
x₁

Для того, чтобы изобразить область Ω, приведем первое неравенство системы ограничений к каноническому виду:

<=> <=>

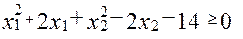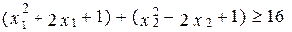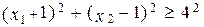-внешняя область плоскости относительно окружности с центром (-1;1) радиуса 4

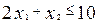- полуплоскость, расположенная левее и ниже прямой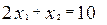

x_1*x₂=h, т.е. x₂₌h/x₁ – семейство гипербол.

Найдем точку пересечения гиперповерхности x_1*x₂=h и прямой x₂=10-2x₁;

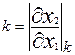- коэффициент угла наклона касательной к гиперповерхности, тогда k=-h/x²; составим и решим систему уравнений:

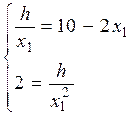т.е. x₁=2,5; x₂=5, тогда α_опт(2,5;5) ƒ(α_опт)=12,5

При условии x_i целочисленности рассмотрим

x₁=2 → x₂=6 → ƒ(α_опт)=ƒ(2;6)=ƒ(3;4)=12

x₁=3 → x₂=4

2. Метод множителей Лагранжа применим, если система ограничений содержит только уравнения, и функции ƒ_i и g_i непрерывны вместе со своими частными производными, то задача является задачей на условный экстремум и решается по алгоритму:

1. Рассматриваем дополнительную функцию Лагранжа, вводя набор дополнительных переменных λ₁, λ₂, … λ_m:

F(λ_i,x_j)=ƒ(x₁, x₂, …, x_n)+ 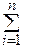λ_i (b_i-g_i (x₁, x₂, …, x_n)).

2. Находим безусловные экстремумы функции F, которые являются решением задачи.

Пример. По плану производства предприятию необходимо изготовить 180 изделий, что возможно двумя способами, производственные функции затрат которых имеют вид 4x₁+x₁² и 8x₂+x₂²; x₁,x₂ – объем продукции произведенных первым и вторым способами соответственно. Найти план производства с минимальными затратами.

Составим математическую модель задачи: x₁+x₂=180; x_i≥0;

ƒ(x₁,x₂)= 4x₁+x₁²+ 8x₂+x₂²→min

Составим функцию Лагранжа: F=4x₁+x₁²+ 8x₂+x₂²+λ(180-(x₁+x₂))

Найдем стационарную точку функции F:

4+2x₁+λ(-1)=0; 8+2x₂+λ(-1)=0; 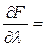180-x₁-x₂=0.

Решив данную систему, получим

λ=186; х₁=91; х₂=89

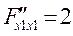
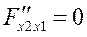
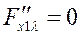
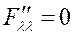
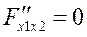
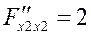
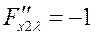
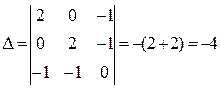
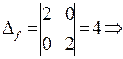ƒ экстремум есть и 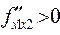→ ƒ(91,89)= min ƒ