Классическое определение вероятности.
В основе классического определения вероятности лежит понятие вероятностного опыта, или вероятностного эксперимента. Его результатом является один из нескольких возможных исходов, называемых элементарными исходами, причем нет оснований ожидать, что какой-либо элементарный исход будет появляться чаще других при повторении вероятностного опыта. Например, рассмотрим вероятностный эксперимент по бросанию игральной кости (кубика). Результатом этого опыта является выпадение одного из 6 очков, нарисованных на гранях кубика.
Таким образом, в этом эксперименте 6 элементарных исходов:
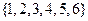 ,
,
и каждый из них равноожидаем.
Событием в классическом вероятностном эксперименте является произвольное подмножество множества элементарных исходов. В рассмотренном примере по бросанию игральной кости событием является, например, выпадение четного числа очков, которое состоит из элементарных исходов 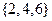 .
.
Вероятностью события 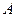 называется число:
называется число:
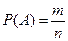 ,
,
где 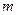 число элементарных исходов, из которых состоит событие
число элементарных исходов, из которых состоит событие 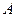 (иногда говорят, что это число элементарных исходов, благоприятствующих появлению события
(иногда говорят, что это число элементарных исходов, благоприятствующих появлению события 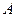 ), а
), а 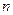 - число всех элементарных исходов.
- число всех элементарных исходов.
В нашем примере:
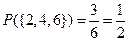 .
.
Элементы комбинаторики.
При описании многих вероятностных опытов элементарные исходы можно отождествить с одним из следующих объектов комбинаторики (науки о конечных множествах).
Перестановкой из 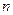 чисел
чисел 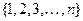 называется произвольная упорядоченная запись этих чисел без повторений. Например, для множества из трех чисел
называется произвольная упорядоченная запись этих чисел без повторений. Например, для множества из трех чисел 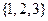 имеется 6 различных перестановок:
имеется 6 различных перестановок:
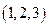 ,
, 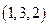 ,
, 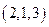 ,
, 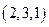 ,
, 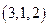 ,
, 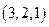 .
.
Для произвольного 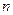 число перестановок равно
число перестановок равно
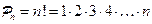
(произведение 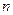 подряд стоящих чисел натурального ряда, начиная с 1).
подряд стоящих чисел натурального ряда, начиная с 1).
Сочетанием из 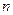 по
по 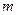 называется произвольный неупорядоченный набор любых
называется произвольный неупорядоченный набор любых 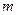 элементов множества
элементов множества 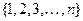 . Например, для множества из трех чисел
. Например, для множества из трех чисел 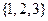 имеется 3 различных сочетания из 3 по 2:
имеется 3 различных сочетания из 3 по 2:
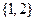 ,
, 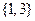 ,
, 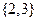 .
.
Для произвольной пары 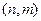 ,
, 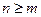 , число сочетаний из
, число сочетаний из 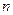 по
по 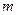 равно
равно
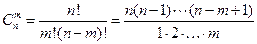 .
.
Например,
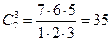 ,
, 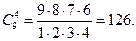
Гипергеометрическое распределение.
Рассмотрим следующий вероятностный опыт. Имеется черный ящик, в котором лежит 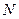 белых и
белых и 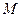 черных шаров. Шары одинакового размера и неотличимы наощупь. Эксперимент состоит в том, что мы наудачу вытаскиваем
черных шаров. Шары одинакового размера и неотличимы наощупь. Эксперимент состоит в том, что мы наудачу вытаскиваем 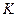 шаров. Событие
шаров. Событие 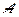 , вероятность которого надо найти, состоит в том, что из этих
, вероятность которого надо найти, состоит в том, что из этих 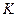 шаров
шаров 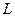 - белые, а остальные
- белые, а остальные 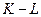 - черные.
- черные.
Перенумеруем все шары числами от 1 до 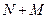 . Пусть числа 1, ¼,
. Пусть числа 1, ¼, 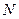 соответствуют белым шарам, а числа
соответствуют белым шарам, а числа 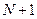 , ¼,
, ¼, 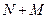 - черным шарам. Элементарным исходом в этом опыте является неупорядоченный набор
- черным шарам. Элементарным исходом в этом опыте является неупорядоченный набор 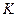 элементов из множества
элементов из множества 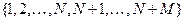 , то есть сочетание из
, то есть сочетание из 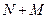 по
по 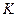 . Следовательно, имеется
. Следовательно, имеется 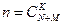 всех элементарных исходов.
всех элементарных исходов.
Найдем число элементарных исходов, благоприятствующих появлению события 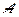 . Соответствующие наборы состоят из
. Соответствующие наборы состоят из 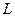 “белых” и
“белых” и 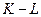 “черных” чисел. Выбрать
“черных” чисел. Выбрать 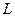 чисел из
чисел из 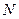 “белых” чисел можно
“белых” чисел можно 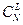 способами, а
способами, а 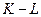 чисел из
чисел из 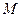 “черных” ¾
“черных” ¾ 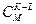 способами. Белые и черные наборы могут соединяться произвольно, поэтому всего имеется
способами. Белые и черные наборы могут соединяться произвольно, поэтому всего имеется 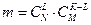 элементарных исходов, благоприятствующих событию
элементарных исходов, благоприятствующих событию 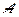 .
.
Вероятность события 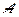 равна
равна
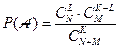 .
.
Полученная формула называется гипергеометрическим распределением.
Задача 5.1. В ящике находится 55 кондиционных и 6 бракованных однотипных деталей. Какова вероятность того, что среди трех наудачу выбранных деталей окажется хотя бы одна бракованная?
Решение. Всего имеется 61 деталь, берем 3. Элементарный исход есть сочетание из 61 по 3. Число всех элементарных исходов равно 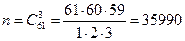 . Благоприятные исходы делятся на три группы: 1) это те исходы, в которых 1 деталь бракованная, а 2 хорошие; 2) 2 детали бракованные, а 1 хорошая; 3) все 3 детали бракованные. Число наборов первого вида равно
. Благоприятные исходы делятся на три группы: 1) это те исходы, в которых 1 деталь бракованная, а 2 хорошие; 2) 2 детали бракованные, а 1 хорошая; 3) все 3 детали бракованные. Число наборов первого вида равно 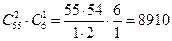 , число наборов второго вида равно
, число наборов второго вида равно 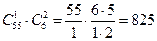 , число наборов третьего вида равно
, число наборов третьего вида равно 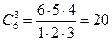 . Следовательно, появлению события благоприятствуют
. Следовательно, появлению события благоприятствуют 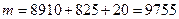 элементарных исходов. Вероятность события равна
элементарных исходов. Вероятность события равна 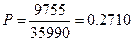
Алгебра событий
Пространством элементарных событий 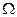 называется множество всех элементарных исходов, относящихся к данному опыту.
называется множество всех элементарных исходов, относящихся к данному опыту.
Суммой 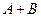 двух событий называется событие, которое состоит из элементарных исходов, принадлежащих событию
двух событий называется событие, которое состоит из элементарных исходов, принадлежащих событию 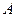 или событию
или событию 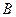 .
.
Произведением 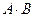 двух событий называется событие, состоящие из элементарных исходов, принадлежащих одновременно событиям
двух событий называется событие, состоящие из элементарных исходов, принадлежащих одновременно событиям 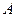 и
и 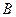 .
.
События 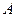 и
и 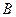 называются несовместными, если
называются несовместными, если 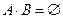 .
.
Событие 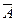 называется противоположным событию
называется противоположным событию 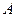 , если событию
, если событию 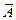 благоприятствуют все те элементарные исходы, которые не принадлежат событию
благоприятствуют все те элементарные исходы, которые не принадлежат событию 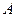 . В частности,
. В частности, 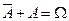 ,
, 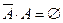 .
.
ТЕОРЕМА о сумме. 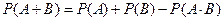
В частности, 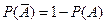 .
.
Условной вероятностью события 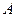 при условии, что событие
при условии, что событие 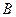 произошло, называется отношение числа элементарных исходов, принадлежащих пересечению
произошло, называется отношение числа элементарных исходов, принадлежащих пересечению 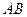 , к числу элементарных исходов, принадлежащих
, к числу элементарных исходов, принадлежащих 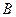 . Иными словами, условная вероятность события
. Иными словами, условная вероятность события 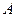 определяется классической формулой вероятности, в которой новым вероятностным пространством является
определяется классической формулой вероятности, в которой новым вероятностным пространством является 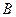 . Обозначается условная вероятность события через
. Обозначается условная вероятность события через 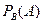 .
.
ТЕОРЕМА о произведении. 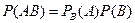 .
.
События называются независимыми, если 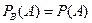 . Для независимых событий теорема о произведении дает соотношение
. Для независимых событий теорема о произведении дает соотношение 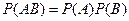 .
.
Следствием теорем о сумме и о произведении является следующие две формулы.
Формула полной вероятности. Полной группой гипотез называется произвольный набор несовместных событий 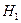 ,
, 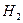 , ¼,
, ¼, 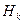 , в сумме составляющих все вероятностное пространство:
, в сумме составляющих все вероятностное пространство:
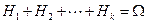 ,
, 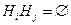 ,
, 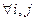 .
.
В этой ситуации для произвольного события 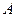 справедлива формула, называемая формулой полной вероятности,
справедлива формула, называемая формулой полной вероятности,
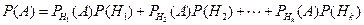 .
.
Формула Байеса позволяет пересчитать вероятность каждой из гипотез, при условии, что событие произошло:
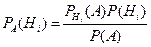
или, более подробно,
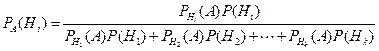 .
.
Задача 5.2. Группа состоит из 6 отличников, 12 хорошо успевающих студентов и 22 студентов, успевающих посредственно. Отличник отвечает на 5 и 4 с равной вероятностью, хорошист отвечает на 5, 4 и 3 с равной вероятностью, и посредственно успевающий студент отвечает на 4, 3 и 2 с равной вероятностью. Случайно выбранный студент ответил на 4. Какова вероятность того, что был вызван посредственно успевающий студент?
Решение. Рассмотрим три гипотезы:
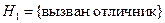 ,
,
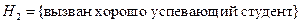
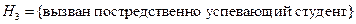 Рассматриваемое событие
Рассматриваемое событие 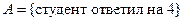 . Из условия задачи известно, что
. Из условия задачи известно, что
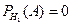 ,
, 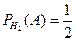 ,
, 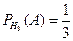 .
.
Найдем вероятности гипотез. Поскольку в группе всего 40 студентов, а отличников 6, то 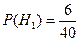 . Аналогично,
. Аналогично, 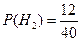 ,
, 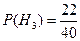 . Применяя формулу полной вероятности, находим
. Применяя формулу полной вероятности, находим
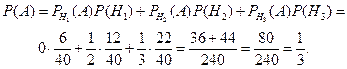
Теперь применим к гипотезе 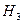 формулу Байеса:
формулу Байеса:
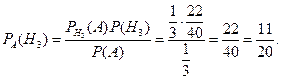
Ответ: 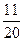 .
.
Испытания Бернулли.
Рассмотрим вероятностный опыт с двумя элементарными исходами. Обычно эти исходы отождествляют с 1 и 0. Вероятность 1 равна 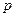 , вероятность 0 равна
, вероятность 0 равна 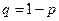 . Стандартным примером является наблюдение за некоторым событием
. Стандартным примером является наблюдение за некоторым событием 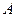 в том или ином вероятностном эксперименте. Тогда, если событие произошло, то полагают, что выпала 1 (успех), а если нет, то 0 (неудача). Испытанием Бернулли называют повторение
в том или ином вероятностном эксперименте. Тогда, если событие произошло, то полагают, что выпала 1 (успех), а если нет, то 0 (неудача). Испытанием Бернулли называют повторение 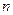 независимых испытаний с двумя исходами. Вопрос состоит в том, чему равна вероятность выпадения
независимых испытаний с двумя исходами. Вопрос состоит в том, чему равна вероятность выпадения 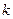 успехов в
успехов в 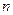 испытаниях.
испытаниях.
Ответ определяется формулой:
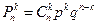 .
.
При больших значениях 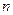 и
и 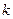 непосредственный подсчет по этой затруднителен. Поэтому применяют приближенную формулу
непосредственный подсчет по этой затруднителен. Поэтому применяют приближенную формулу
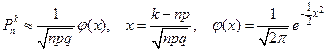
(соответствующее утверждение называют локальной теоремой Муавра-Лапласа). Если требуется найти сумму 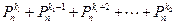 , то можно использовать асимптотическую формулу из интегральной теоремы Муавра-Лапласа
, то можно использовать асимптотическую формулу из интегральной теоремы Муавра-Лапласа
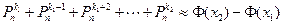 ,
,
где 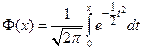 есть функция Лапласа,
есть функция Лапласа, 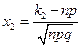 ,
, 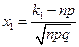 . Функция Лапласа затабулирована, и ее значения при заданном
. Функция Лапласа затабулирована, и ее значения при заданном 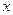 можно найти в любом учебнике по теории вероятности и математической статистике.
можно найти в любом учебнике по теории вероятности и математической статистике.
Задача 5.3. Известно, что в большой партии деталей имеется 11% бракованных. Для проверки выбирается 100 деталей. Какова вероятность того, что среди них найдется не более 14 бракованных? Оценить ответ с использованием теоремы Муавра-Лапласа.
Решение. Мы имеем дело с испытанием Бернулли, где 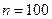 ,
, 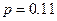 ,
, 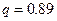 . Успехом считается обнаружить бракованную деталь, и число успехов удовлетворяет неравенству
. Успехом считается обнаружить бракованную деталь, и число успехов удовлетворяет неравенству 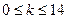 . Следовательно,
. Следовательно,
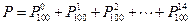 .
.
Прямой подсчет дает:
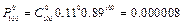 ,
, 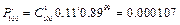 ,
, 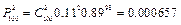 ,
, 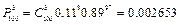 ,
, 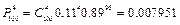 ,
, 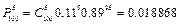 ,
, 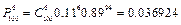 ,
, 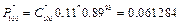 ,
, 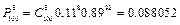 ,
, 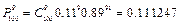 ,
, 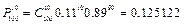 ,
, 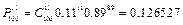 ,
, 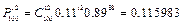 ,
, 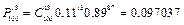 ,
, 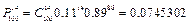 .
.
Следовательно, 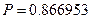 . Теперь применим интегральную теорему Муавра-Лапласа. Получаем:
. Теперь применим интегральную теорему Муавра-Лапласа. Получаем:
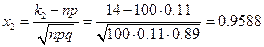 ,
, 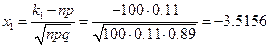 .
.
Используя таблицу значений функции 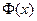 , с учетом нечетности функции, получаем
, с учетом нечетности функции, получаем
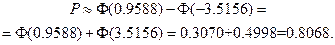
Ошибка приближенного вычисления не превышает 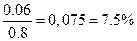 .
.
Случайные величины
Случайной величиной называется числовая характеристика вероятностного опыта, которая является функцией от элементарных исходов. Если 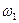 ,
, 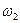 , ¼,
, ¼, 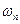 есть множество элементарных исходов, то случайная величина
есть множество элементарных исходов, то случайная величина 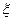 есть функция
есть функция 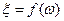 . Удобнее, однако, охарактеризовать случайную величину
. Удобнее, однако, охарактеризовать случайную величину 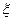 , перечислив все ее возможные значения
, перечислив все ее возможные значения 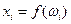 и вероятности, с которыми она принимает это значение
и вероятности, с которыми она принимает это значение 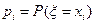 .
.
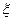 | 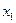 | 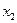 | ¼ | 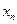 |
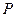 | 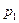 | 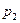 | ¼ | 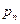 |
Такая таблица называется законом распределения случайной величины. Поскольку события 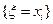 образуют полную группу, выполнен закон вероятностной нормировки
образуют полную группу, выполнен закон вероятностной нормировки
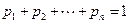 .
.
Математическое ожидание, или среднее значение, случайной величины 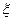 есть число, равное сумме произведений значений случайной величины на соответствующие вероятности.
есть число, равное сумме произведений значений случайной величины на соответствующие вероятности.
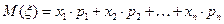
Дисперсия (степень разброса значений вокруг математического ожидания) случайной величины 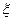 есть математическое ожидание случайной величины
есть математическое ожидание случайной величины 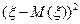 ,
,
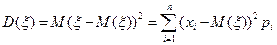 .
.
Можно показать, что
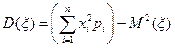
Величина
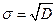
называется средним квадратичным уклонением случайной величины 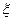 .
.
Функцией распределения 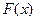 для случайной величины
для случайной величины 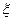 есть вероятность попасть на множество
есть вероятность попасть на множество 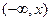 , то есть
, то есть
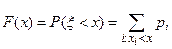 .
.
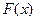 является неотрицательной, неубывающей функцией, принимающей значения от 0 до 1. Для случайной величины, имеющей конечное множество значений,
является неотрицательной, неубывающей функцией, принимающей значения от 0 до 1. Для случайной величины, имеющей конечное множество значений, 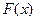 является кусочно-постоянной функцией, имеющие разрывы второго рода в точках состояний
является кусочно-постоянной функцией, имеющие разрывы второго рода в точках состояний 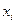 . При этом
. При этом 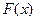 непрерывна слева и
непрерывна слева и 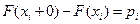 .
.
Задача 5.4. Производится последовательное бросание двух игральных костей. При выпадении на одной игральной кости одного, трех или пяти очков игрок лишается 5 рублей. При выпадении двух или четырех очков игрок получает 7рублей. При выпадении шести очков игрок лишается 12рублей. Случайная величина x есть выигрыш игрока при двух бросаниях костей. Найти закон распределения x, построить график функции распределения, найти математическое ожидание и дисперсию x.
Решение. Рассмотрим сначала, чему равен выигрыш игрока при одном бросании кубика. Пусть событие 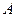 состоит в том, что выпало 1, 3 или 5 очков. Тогда
состоит в том, что выпало 1, 3 или 5 очков. Тогда 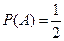 , а выигрыш составит
, а выигрыш составит 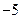 рублей. Пусть событие
рублей. Пусть событие 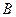 состоит в том, что выпало 2 или 4 очка. Тогда
состоит в том, что выпало 2 или 4 очка. Тогда 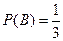 , а выигрыш составит
, а выигрыш составит 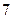 рублей. Наконец, пусть событие
рублей. Наконец, пусть событие 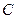 означает выпадение 6 очков. Тогда
означает выпадение 6 очков. Тогда 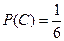 и выигрыш равен
и выигрыш равен 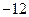 рублей.
рублей.
Теперь рассмотрим все возможные комбинации событий 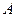 ,
, 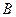 и
и 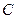 при двух бросаниях кости, и определим значения выигрыша
при двух бросаниях кости, и определим значения выигрыша 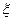 при каждой такой комбинации.
при каждой такой комбинации.
Если произошло событие 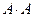 , то
, то 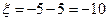 , при этом
, при этом 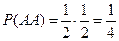 .
.
Если произошло событие 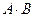 , то
, то 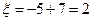 , при этом
, при этом 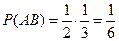 .
.
Если произошло событие  , то
, то 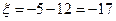 , при этом
, при этом 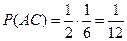 .
.
Аналогично, при 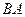 получаем
получаем 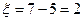 ,
, 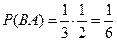 .
.
При 
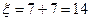 ,
, 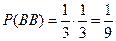 .
.
При 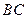
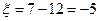 ,
, 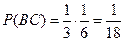 .
.
При 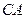
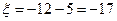 ,
, 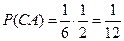 .
.
При 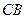
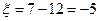 ,
, 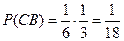 .
.
При 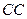
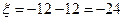 ,
, 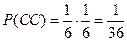 .
.
Все найденные состояния 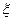 и суммарные вероятности этих состояний записываем в таблицу:
и суммарные вероятности этих состояний записываем в таблицу:
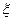 | 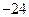 | 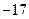 | 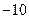 | 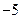 | ||
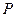 | 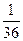 | 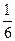 | 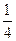 | 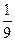 | 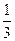 | 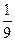 |
Проверяем выполнение закона вероятностной нормировки:
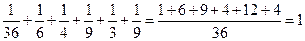 .
.
Найдем математическое ожидание  :
:
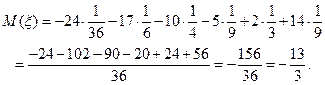
Найдем дисперсию
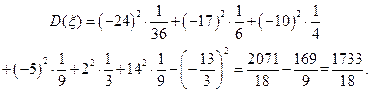
Функция распределения случайной величины имеет вид
 |
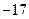
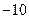
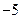 2 14
2 14 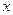
Непрерывные случайные величины.
Если случайная величина принимает бесконечно много значений, например, все значения из некоторого интервала, то ее закон распределения определяется следующим образом. Мы должны определить вероятность любого события, связанного с данной случайной величиной. В частности, для произвольного интервала 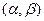 на вещественной прямой нужно уметь определить вероятность попадания случайной величины в этот интервал
на вещественной прямой нужно уметь определить вероятность попадания случайной величины в этот интервал
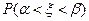 .
.
Проще всего это сделать через функцию распределения случайной величины 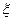 . Пусть, по—прежнему,
. Пусть, по—прежнему,
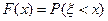 .
.
Тогда
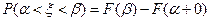
(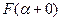 обозначает предел справа функции
обозначает предел справа функции 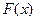 в точке
в точке 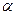 ). Таким образом, закон распределения непрерывной случайной величины определяется функцией распределения
). Таким образом, закон распределения непрерывной случайной величины определяется функцией распределения 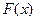 .
.
Для многих стандартных законов распределения функция 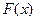 выглядит достаточно громоздко, и, кроме того, не выражается через элементарные функции. Для определения закона распределения часто используют функцию плотности распределения:
выглядит достаточно громоздко, и, кроме того, не выражается через элементарные функции. Для определения закона распределения часто используют функцию плотности распределения:
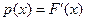 .
.
Тогда, если функция 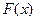 оказывается дифференцируемой, то:
оказывается дифференцируемой, то:
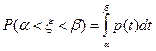 .
.
В частности,
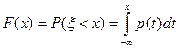
Поскольку функция распределения 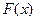 является не убывающей, то
является не убывающей, то 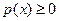 . Условие вероятностной нормировки
. Условие вероятностной нормировки 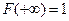 сводится к тому, что
сводится к тому, что
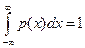 .
.
Математическое ожидание непрерывно распределенной случайной величины равно
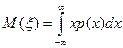 .
.
Дисперсия определяется формулой
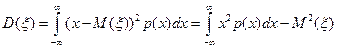 .
.
Полезно запомнить следующие три стандартных закона распределения.
1) Равномерное распределение. Функция плотности имеет вид:
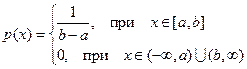
Математическое ожидание равномерного закона равно 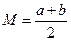 (это в точности середина отрезка распределения), а дисперсия
(это в точности середина отрезка распределения), а дисперсия 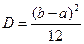 .
.
2) Пуассоновское распределение. Функция плотности имеет вид:
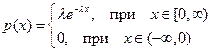
Математическое ожидание пуассоновского распределения равно 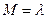 , а дисперсия
, а дисперсия 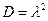 .
.
3) Нормальное распределение. Функция плотности имеет вид
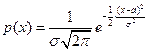 .
.
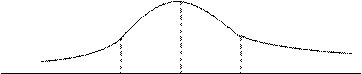
Наиболее важным законом является нормальный закон распределения. График функции плотности нормального закона представляет собой колоколообразную кривую, имеющую наибольшее значение в точке 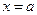 и быстро убывающую при
и быстро убывающую при 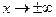 . В частности, справедливо правило
. В частности, справедливо правило 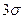 : 99% площади фигуры, заключенной между графиком плотности нормального закона и осью абсцисс, приходится на отрезок
: 99% площади фигуры, заключенной между графиком плотности нормального закона и осью абсцисс, приходится на отрезок 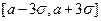 . Математическое ожидание нормального закона равно
. Математическое ожидание нормального закона равно 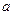 , а дисперсия равна
, а дисперсия равна 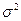 .
.
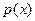
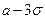
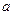
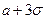
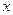
Значение нормального закона распределения для теории вероятности и математической статистики определяется центральной предельной теоремой Ляпунова. Пусть
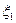 ,
, 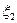 , ¼,
, ¼, 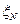
независимые, одинаково распределенные случайные величины с произвольным законом распределения. Если 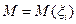 - математическое ожидание, а
- математическое ожидание, а 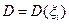 дисперсия этих случайных величин, то случайная величина
дисперсия этих случайных величин, то случайная величина
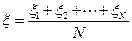
при 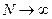 распределена асимптотически нормально с показателями
распределена асимптотически нормально с показателями 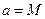 ,
, 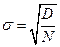 . Это означает, что при любых фиксированных
. Это означает, что при любых фиксированных 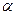 ,
, 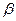
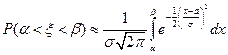 .
.
Точнее, при 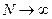 предел отношения правой и левой частей формулы равен 1.
предел отношения правой и левой частей формулы равен 1.
Задача 5.5. Для случайной величины, распределенной по закону косинуса с плотностью
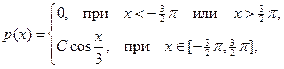
найти константу С, вероятность попадания в интервал (- 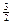 p,
p, 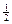 p), а также математическое ожидание и дисперсию.
p), а также математическое ожидание и дисперсию.
Решение. С учетом вероятностной нормировки 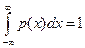 , получаем
, получаем
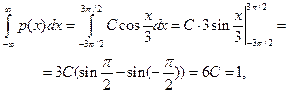
следовательно, 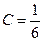 .
.
Вероятность попадания в интервал есть интеграл от плотности по этому интегралу,
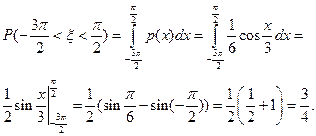
Математическое ожидание равно:
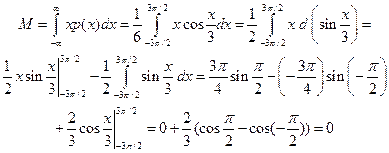
(впрочем, это было очевидно с самого начала, поскольку мы интегрируем нечетную функцию по симметричной относительно начала координат области).
Дисперсия равна:
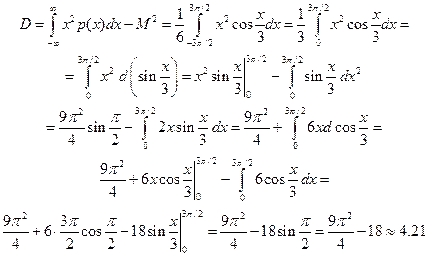
 2015-05-13
2015-05-13 10308
10308







