(F1, F2,...,Fn)~R => для равновесия тела, находящегося под действием системы сходящихся сил, необходимо и достаточно, чтобы их равнодействующая равнялась нулю: R = 0. Следовательно, в силовом многоугольнике уравновешенной системы сходящихся сил конец последней силы должен совпадать с началом первой силы; в этом случае говорят, что силовой многоугольник замкнут (рис. 2.3). Это условие используется при графическом решении задач для плоских систем сил. Векторное равенство R=0 эквивалентно трем скалярным равенствам: Rx=åFkx=F1x+F2x+…+Fnx=0; Ry=åFky=F1y+F2y+…+Fny=0; Rz=åFkz=F1z+F2z+…+Fnz=0; где Fkx, Fky, Fkz– проекции силы Fk на оси, а Rx, Ry, Rz– проекции равнодействующей на те же оси. Т. е. для равновесия сходящейся системы сил необходимо и достаточно равенства нулю алгебраических сумм проекций всех сил данной системы на каждую из координатных осей. Для плоской системы сил пропадает условие, связанное с осью Z. Условия равновесия позволяют проконтролировать, находится ли в равновесии заданная система сил.
5)Параллельные силы 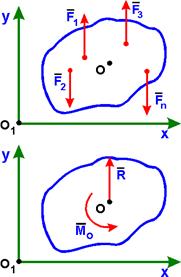 в плоскости
в плоскости
|
|
|
Система сил F1, F2,..., Fn, лежащих в одной плоскости, линии действия которых параллельны друг другу, называется плоской системой параллельных сил.
При приведении этой системы сил к произвольному центру (точке) О получим главный вектор R, приложенный в точке О, и пару сил с моментом Mo.
Главный вектор R системы параллельных сил параллелен силам, его модуль равен абсолютному значению алгебраической суммы проекций сил на ось (О1у), параллельную силам, а его направление определяется знаком этой суммы:
| R | = | Ry | = |S±Fk |. (k = 1, 2,..., n)
Момент пары сил Mo равен главному моменту параллельных сил F1, F2,..., Fn относительно центра приведения О:
Mo = S mo(Fk). (k = 1, 2,..., n)
Условия равновесия для плоской системы параллельных сил имеют вид:
R = 0, Mo = 0.
Из них следуют две формы аналитических условий равновесия для системы параллельных сил на плоскости.
 1. Основная форма условий равновесия.
1. Основная форма условий равновесия.
S Fky = S±Fky = 0, S mo(Fk) = 0. (k = 1, 2,..., n)
для равновесия плоской системы параллельных сил необходимо и достаточно, чтобы сумма проекций сил на ось, параллельную силам, и сумма их моментов относительно точки, лежащей на плоскости действия сил, были равны нулю.
2. Вторая форма условий равновесия:
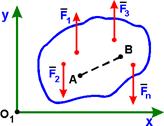 S mА(Fk) = 0, S mВ(Fk) = 0. (k = 1, 2,..., n)
S mА(Fk) = 0, S mВ(Fk) = 0. (k = 1, 2,..., n)
Для равновесия плоской системы параллельных сил необходимо и достаточно, чтобы суммы моментов всех сил относительно любых двух точек А и В (причем прямая АВ не параллельна силам), были равны нулю.
Для плоской системы параллельных сил каждая форма содержит два уравнения равновесия.
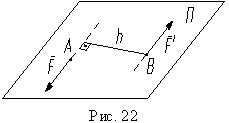 6)Пара сил,момент пары,свойства пар.
6)Пара сил,момент пары,свойства пар.
- это система двух равных параллельных сил, направленных в разные стороны (рис. 22).
|
|
|
Кратчайшее расстояние между линиями действия сил называют плечом пары h, а плоскость П, где лежит пара сил, является плоскостью пары.
Пары сил реально существуют в природе. Ярким примером являются силы, действующие на стороны рамки с током в магнитном поле. На этом физическом явлении основана работа всех электродвигателей постоянного тока.
Свойства пары сил. Сформулируем, а затем докажем первое свойство.
 Первое свойство. Пару сил нельзя привести к силе. Иными словами пара сил (как и сила) является самостоятельным элементом статики.
Первое свойство. Пару сил нельзя привести к силе. Иными словами пара сил (как и сила) является самостоятельным элементом статики.
При изучении динамики мы покажем, что под действием пары сил свободное твердое тело может только поворачиваться. Следовательно, в этом параграфе мы будем изучать свойства нового самостоятельного элемента статики, под действием которого, в отличие от силы, свободное твердое тело может только поворачиваться.
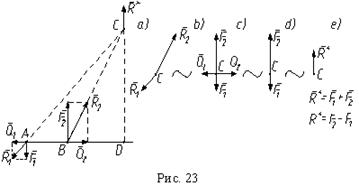
Для доказательства рассмотрим сложение параллельных сил. Сложим две неравные параллельные силы, направленные в разные стороны (рис. 23). Добавляем к исходной системе сил (F1,F2) уравновешенную систему сил (Q1,Q2) ~ 0. По аксиоме параллелограмма, силы, приложенные в точках A и B, эквивалентны двум непараллельным силам R1 и R2 (рис. 23, a). Согласно следствию второй аксиомы, переносим эти силы в точку пересечения их линий действия C (рис. 23, b). Используя вторую и третью аксиомы, раскладываем силы R1 и R2 на составляющие (рис. 23, c), а затем вычитаем уравновешенную систему сил (Q1,Q2). В результате получаем, что исходная система сил эквивалентна тем же силам, но приложенным в одной точке C, то есть (F1,F2) = (F1,F2)C (рис. 23, d). По аксиоме параллелограмма эта система, а следовательно, и исходная система сил, эквивалентна одной силе или равнодействующей (рис. 23, c): (1)
Из рисунков видим, что равнодействующая и ее линия действия CD параллельны исходным силам, а точка D лежит вне отрезка AB.
При сложении двух параллельных сил, направленных в одну сторону, получается аналогичный результат, только величина равнодействующей будет равна R* = F1 + F2, а точка D будет лежать внутри отрезка AB.
Можно распространить этот вывод и на систему из n параллельных сил, добавляя к полученной равнодействующей по одной из оставшихся сил системы. В результате мы докажем, что система параллельных сил приводится к одной силе или равнодействующей. Вопрос нахождения линии действия равнодействующей будет подробно рассмотрен в теме о центре параллельных сил.
Вернемся к доказательству первого свойства пары сил. Устремим величину первой силы ко второй. При F1 F1 из выражений (1) следует, что R* 0, а по рис. 22, a видим, что AC и BC становятся параллельны друг другу. Следовательно, пара сил не может быть приведена к силе или равнодействующей, так как равнодействующая не имеет величины, а ее линия действия не определена, потому что нельзя найти точку C. Таким образом, свойство доказано.
 Второе свойство. Действие пары сил на твердое тело определяется моментом пары, который является свободным вектором, перпендикулярным плоскости пары, численно равным произведению силы на плечо пары.
Второе свойство. Действие пары сил на твердое тело определяется моментом пары, который является свободным вектором, перпендикулярным плоскости пары, численно равным произведению силы на плечо пары.
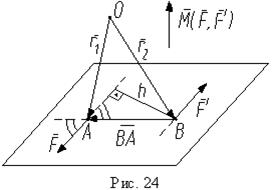
Ранее мы показали, что пара сил не может быть приведена к силе, а является самостоятельным элементом статики. Выясним, как пара сил действует на твердое тело. Выберем в пространстве произвольный центр O (рис. 24) и вычислим относительно этого центра сумму моментов сил, образующих пару. Эту сумму мы назовем моментом пары. Положение точек приложения сил пары относительно центра O определим радиус-векторами r1, r2 и, учитывая, что F' = -F, получим (2)
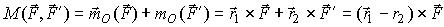
Строим вектор BA, который определяет положение точки A относительно B, и на рис. 24 видим, что r1 = r + BA или r1 - r = BA. Учитывая это, из выражения (2) получаем (3)
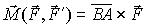
Таким образом, действие пары сил на тело определяется ее моментом, который является мерой действия пары сил на твердое тело.
|
|
|
Так как центр O выбран произвольно, то момент пары не зависит от выбора центра, то есть является свободным вектором. По определению векторного произведения он перпендикулярен плоскости пары (в этой плоскости лежат перемножаемые векторы BA и F) и направлен так, что с его конца вращение тела под действием пары сил наблюдается против хода часов (как и вращение BA к F по кратчайшему угловому расстоянию). Это отражено на рис. 24. Величину момента пары найдем, определяя модуль векторного произведения в (3), учитывая (рис. 24), что BA sin(BA ^ F) = h: (4)
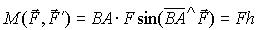
Приняв за центр O последовательно точки приложения сил A и B, по формуле (2) имеем (5)
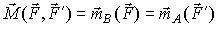
Эта формула имеет важное значение при решении задач, когда нужно вычислять суммы моментов пар сил относительно точки.
Так как момент пары является свободным вектором, то он не имеет фиксированной точки приложения, а имеет только свой модуль и свое направление и приложить его можно в любой точке твердого тела. Это принципиальное отличие момента пары от момента силы относительно центра (точки), являющегося связанным вектором, приложенным в центре, и от скользящего вектора, примером которого является сила, приложенная к твердому телу, которую можно переносить только вдоль линии ее действия.
Следствия из второго свойства пары.
1. Действие пары на твердое тело не изменяется, если пару сил поворачивают в плоскости пары. Очевидно, что при этом момент пары не изменяется.
2. Действие пары сил на твердое тело не изменяется, если пару сил переносят в другое место плоскости пары. Это соответствует переносу момента пары, как свободного вектора, параллельно плоскости пары.
3. Действие пары сил на твердое тело не изменяется, если ее перенести в плоскость, параллельную плоскости пары. То есть момент пары, как свободный вектор, переносится перпендикулярно плоскости пары.
Эти на первый взгляд парадоксальные свойства пары сил поясним физическими примерами. Гаечный ключ одинаково действует на гайку, к каким бы граням этой гайки его не приложить - момент пары не изменяется от поворота пары сил в плоскости пары. Трансмиссионный вал передает шкиву вращающий момент независимо от места закрепления шкива на валу - момент пары сил не изменяется от ее переноса в плоскость, параллельную плоскости пары.
|
|
|
Моменты пар рассматриваются как векторы, когда пары сил лежат в различных плоскостях. В плоской системе сил, когда все силы и пары сил лежат в одной плоскости, моменты пар направлены перпендикулярно этой плоскости и поэтому параллельны друг другу. Естественно, что в этом случае, момент пары удобнее рассматривать как алгебраическую величину, равную (6)
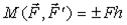
Момент пары будет положительной величиной, если пара сил стремиться повернуть тело против хода часов и отрицательной, если она поворачивает тело по ходу часов.
Эквивалентность пар сил. Две пары сил с равными моментами эквивалентны. Или (F,F') ~ (P,P'), если M(F,F') ~ M(P,P'). Эквивалентность пар сил сразу следует из свойств пары сил. Очевидно, что только при равных моментах пар сил их действие на твердое тело будет одинаковым.
Следует отметить, что силы, образующие пары могут быть не равны между собой F P, но обе пары сил должны лежать в одной плоскости. Это замечание и понятие эквивалентности пар сил позволяют сформулировать правило трансформирования пары сил.
При трансформировании пары сил можно менять величины сил и плечо пары так, чтобы величина момента пары не изменялась, и переносить пару сил согласно следствиям из 2-го свойства.
Моментом силы относительно точки
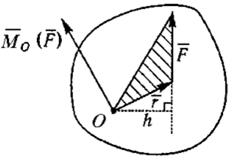 7) Моментом силы относительно точки (рисунок 1.1) называется векторное произведение радиус-вектора точки приложения силы на вектор силы.
7) Моментом силы относительно точки (рисунок 1.1) называется векторное произведение радиус-вектора точки приложения силы на вектор силы.
Mo(F) = r ⊗ F
Рисунок 1.1
Вектор момента направлен перпендикулярно плоскости, в которой лежат сила и точка, в ту сторону, откуда поворот от действия силы виден происходящим против хода часовой стрелки. Вектор момента характеризует положение плоскости и направление вращательного действия силы, а также дает меру этого действия:
|Mo(F)| = F⋅r⋅sinα = F⋅h,
где h – плечо силы (кратчайшее расстояние от точки O – центра момента – до линии действия силы). Если сила проходит через точку, то ее момент относительно этой точки равен нулю.
Момент силы относительно точки не меняется от переноса силы вдоль линии ее действия.
Если силы расположены в одной плоскости, то используется понятие алгебраического момента силы. Алгебраическим моментом силы относительно точки (или центра) называется взятое со знаком плюс или минус произведение модуля силы на плечо (рисунок 1.2).
Знак плюс выбирается в том случае, если сила стремится поворачивать плоскость относительно центра момента против хода часовой стрелки.
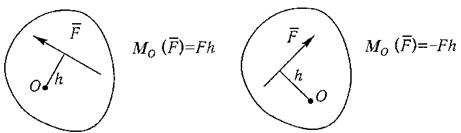
Рисунок 1.2
Если сила F задана своими проекциями Fx, Fy, Fz на оси координат и даны координаты x, y, z точки приложения этой силы, то момент силы относительно начала координат вычисляется следующим образом:
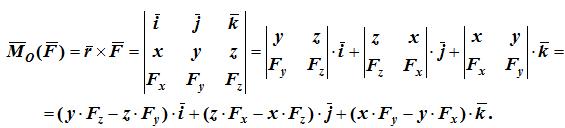
Проекции момента силы на оси координат равны
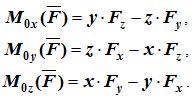
 2015-05-30
2015-05-30 1346
1346








