| Содержание | |
| Рекомендуемая литература | |
| §1. Неопределенный интеграл………………………………………………..…... | |
| §2. Методы интегрирования………………………………………………...…….. 2.1. Непосредственное интегрирование……………………………………... 2.2. Метод подстановки (замены переменных)…………………………….. 2.3. Интегрирование по частям……………………………………….……… | |
| §3. Интегрирование рациональных дробей……………………………..……..… | |
§4. Интегрирование некоторых тригонометрических функций……………..….
4.1. Интеграл вида 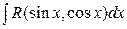 ………………………………………….
4.2. Интеграл произведения синусов и косинусов различных аргументов.
4.3. Вычисление интегралов типа ………………………………………….
4.2. Интеграл произведения синусов и косинусов различных аргументов.
4.3. Вычисление интегралов типа 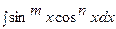 …………………………… ……………………………
| |
§5 Интегрирование некоторых иррациональных функций ……………….
5.1. Интеграл вида 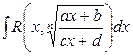 где n- натуральное число…..………..
5.2. Квадратичные иррациональности………………………………………
5.3. Тригонометрическая подстановка……………………………………….
5.4. Интегралы вида где n- натуральное число…..………..
5.2. Квадратичные иррациональности………………………………………
5.3. Тригонометрическая подстановка……………………………………….
5.4. Интегралы вида 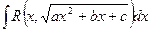 ……………………………………..
5.5. Интегрирование дифференциальных биномов………………………… ……………………………………..
5.5. Интегрирование дифференциальных биномов…………………………
| |
| §6. Определенный интеграл…………………………………………………. 6.1. Свойства определенного интеграла……………………………………. | |
| §7. Вычисление определенного интеграла………………………………….. 7.1. Замена переменных………………………………………………………. 7.2. Интегрирование по частям………………………………………………. | |
| §8. Несобственные интегралы……………………………………………….. | |
| §9. Геометрические приложения определенного интеграла………………. 9.1. Вычисление площадей плоских фигур…………………………………. 9.2. Нахождение площади криволинейного сектора……………………….. 9.3. Вычисление длины дуги кривой………………………………………… 9.4. Объем тел вращения……………………………………………………. | |
| §10. Приближенное вычисление определенного интеграла. Формула парабол. (формула Симпсона или квадратурная формула)………………… | |
| §10. Основные типы интегралов и методы их вычисления………………… | |
| Аудиторная контрольная работа по теме «Неопределенный интеграл»… | |
| Типовой расчет по теме «Определенный интеграл»……………………….. | |
| Тест по теме «Неопределенный и определенный интеграл»……………… |
Рекомендуемая литература
1. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах: Учеб. Пособие для студентов втузов. В 2-х ч. Ч. I. 4-е изд., испр. и доп. – М.: Высш. шк., 1986. – 304 с.
2. Письменный Д.Т. Конспект лекций по высшей математике: Полный курс. – М.: Айрис-пресс, 2004. –608 с.
3. Ларин, А.А. Курс высшей математики. [Текст] / А.А. Ларин. – М.: Высшая школа, 2001. – 257 с.
4. Минорский В.П. Сборник задач по высшей математике: Учеб. Пособие для втузов. – М.: Издательство Физико-математической литературы, 2000. – 336 с.
5. Пискунов Н.С. Дифференциальное и интегральное исчисления для втузов, т.2: М.: Наука, Главная редакция Физико-математической литературы, 1985. – 560 с.
Интегральное исчисление – раздел математики, в котором изучаются свойства, способы вычисления интегралов и их приложения. Центральными понятиями интегрального исчисления являются понятия определённого интеграла и неопределённого интеграла функций одного действительного переменного. Интеграл (от лат. integer — целый), одно из самых важных понятий математики, появившееся в связи с возникшей потребностью, с одной стороны, находить функции по их производным (к примеру, находить функцию, которая выражала бы путь, пройденный движущейся точкой, исходя из скорости этой точки), а с другой — находить площади, объёмы, длины дуг, работу сил за определённый промежуток времени и т. п.
. §1 Неопределенный интеграл
Определение: Функция F(x) называется первообразной функцией функции f(x) на отрезке [a, b], если в любой точке этого отрезка верно равенство:
F¢(x) = f(x).
Надо отметить, что первообразных для одной и той же функции может быть бесконечно много. Они будут отличаться друг от друга на некоторое постоянное число.
F1(x) = F2(x) + C.
Определение: Неопределенным интегралом функции f(x) называется совокупность первообразных функций, которые определены соотношением:
F(x) + C.
Записывают: 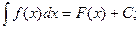
Условием существования неопределенного интеграла на некотором отрезке является непрерывность функции на этом отрезке.
Свойства:
1. 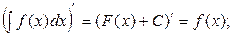
2. 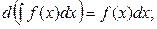
3. 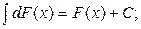
4. 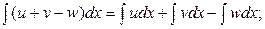 где u, v, w – некоторые функции от х.
где u, v, w – некоторые функции от х.
5. 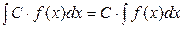
Пример. 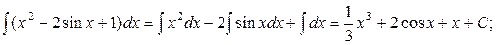
Нахождение значения неопределенного интеграла связано главным образом с нахождением первообразной функции. Для некоторых функций это достаточно сложная задача.
Для удобства значения неопределенных интегралов большинства элементарных функций собраны в специальные таблицы интегралов. Приведем таблицу основных интегралов, с помощью которой можно получить значения неопределенных интегралов различных функций.
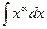 = =
| 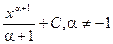
| 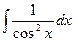 = =
| tgx + C | ||
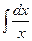 = =
| 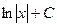
| 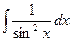 = =
| -ctgx + C | ||
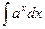 = =
| 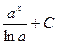
| 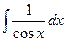 = =
| 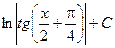
| ||
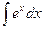 = =
| ex + C | 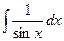 = =
| 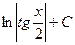
| ||
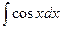 = =
| sinx + C | 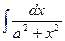 = =
| 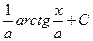
| ||
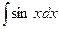 = =
| -cosx + C | 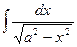 = =
| arcsin 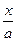 + C + C
| ||
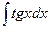 = =
| -ln½cosx½+C | 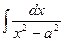 = =
| 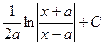
| ||
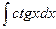 = =
| ln½sinx½+ C | 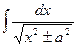 = =
| ln 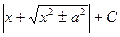
|
 2015-05-30
2015-05-30 617
617







