однородного линейного уравнения

Определение. Две функции y₁(x) и y₂(x) называется линейно независимыми на ]a; b[, если их отношение на этом отрезке не является постоянной величиной, т.е. если 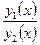¹ const.

В противном случае функции y₁(x) и y₂(x) называются линейно зависимыми.

Примеры 1) Функции y_I(x) = e^x и y₂(x) = e^2x будут линейно независимыми, т.к. 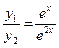¹ const.

2) Функции y_I(x)=cosx; y₂(x)=5cosx – линейно зависимые, т.к. .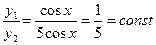

Определение. Если y₁ и y₂ – функции от x, то определитель

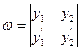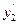= y₁ – y₂y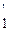

называется определителем Вронского или вронскианом данных функций.

Теорема. 1. Если функции y₁ и y₂ – линейно зависимые функции на ]a; b[, то определитель Вронского на этом интервале тождественно равен нулю.

Действительно, если y₂ = l y₁, где l - const, то

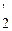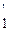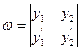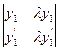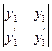y = l y и w (y₁ y₂) = = = l = 0

Приведём ещё одну теорему без доказательства.

Теорема.2. Если функции y₁ и y₂ – линейно зависимые функции на ]a; b[, то определитель Вронского w (y₁ y₂), составленный для этих функций, не обращается в нуль ни в одной точке указанного интервала.

Рассмотрим линейное однородное дифференциальное уравнение второго порядка:

a₀ (x) y^II + a₁ (x)y^I + a₂ (x)y = 0

Так как a₀ (x) ¹ 0, то, разделив обе части этого уравнения на a₀, получим:

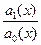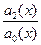y^II + y^I + y = 0

Обозначим 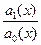=a (x), 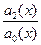=b (x)

Получим: y^II + a (x) y^I + b (x)y = 0 (6).

Теорема (о структуре общего решения линейного однородного дифференциального уравнения второго порядка): если y₁ и y₂ – два линейно независимых решения уравнения (6), то

y = c₁у₁ + с₂у₂ (7),

где с₁ и c₂ – произвольные постоянные, есть его общее решение.

Дано: y₁(x) и y₂ (x) – линейно независимые решения уравнения (6), т.е

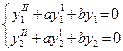и 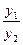¹ const.

Доказать: y = c₁y₁ (x) + c₂y₂ (x) – общее решение уравнения.

Покажем сначала, что y = c₁y₁ + c₂y₂ – решение уравнения (6). Для этого найдём y^I и y^II и подставим выражение y, y^I, y^II в уравнение (6).

y = c₁y₁ + c₂y₂

y^I = c₁ 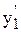+ c₂y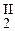

y^II = c₁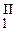y + c₂y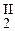

c₁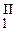y + c₂y 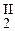+ a (c₁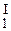y + c₂y 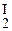) + b (c₁y₁ + c₂y₂) = c₁( 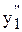+ ay 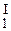+ by₁) +

c₂ 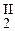(y + ay 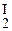+ by₂) = 0, т.к. по условию теоремы y 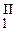+ a 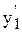+ by₁ = 0 и

y₂^II + ay 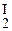+ by₂ = 0.

Итак, y = c₁y₁+c₂y₂ – решение уравнения (6) при любых значениях c₁ и c₂.

Теперь докажем, что решение, y = c₁y₁ + c₂y₂ есть общее решение уравнения (6), т.е. докажем, что каковы бы ни были начальные условия

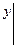
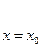
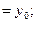и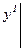

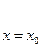
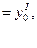
можно так подобрать значения произвольных постоянных c₁ и c₂, чтобы соответствующее частное решение c₁y₁ + c₂y₂ удовлетворяло заданным начальным условиям. Подставляя начальные условия в равенство (7), будем иметь:

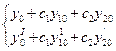(8), где обозначено

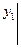
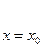= у₁₀,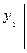

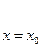
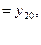
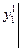
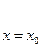
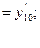и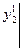

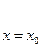
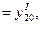
Из системы (8) можно определить c₁ и c₂, так как определитель системы есть определитель Вронского при x = x₀ и, следовательно, не равен нулю (в силу линейной независимости y₁ и y₂).

Частное решение, которое получится из семейства (7) при найденных значениях c₁ и c₂, удовлетворяет заданным начальным условиям. Таким образом, теорема доказана.

Доказанная теорема важна, т.к. сводит задачу нахождения общего решения уравнения (6) к более простой задаче: нахождения двух линейно независимых частных решений.

Пример. Составить общее решение уравнения y^II + 2y = 0, если y₁ = 1 и y₂ = e^-2x его частные линейные независимые решения.

Из теоремы следует, что общее решение y = c₁ y₁ + c₂ y_2.

В нашем случае: y = c₁1 + c₂e^-2x, т.е. y = c₁+ c₂e^-2x - общее решение данного уравнения.

Пусть в уравнении (6) a(x) и b(x) - постоянные числа. Обозначим a(x)=p, b(x)=q, в этом случае и получим: y^II + py^I + qy = 0 – линейное однородное дифференциальное уравнение второго порядка с постоянными коэффициентами (p и q - постоянные числа).

Итак, общим решением однородного уравнения является y = c₁y₁ + c₂y₂.