Постановка задачи и основные определения

Здесь мы рассмотрим случаи, когда множество допустимых решений X задается равенствами и неравенствами, т. е.

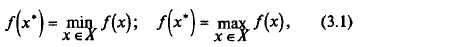
где 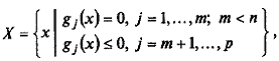m и p — числа; f (х) — целевая функция, g_j (x), j = 1, …, p — функции, задающие ограничения (условия).

Будем считать функции f (х); g_j (x), j = 1, …, p дважды непрерывно дифференцируемыми на множестве Rⁿ. При р = т задача (3.1) со смешанными ограничениями преобразуется в задачу с ограничениями типа равенств, а при т = 0 в задачу с ограничениями типа неравенств

Определение 3. 1. Функция

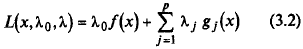
называется обобщенной функцией Лагранжа, числа λ₀, λ₁, …, λ _р — множителями Лагранжа, λ = (λ₁, …, λ _р) ^T .

Классической функцией Лагранжа называется функция

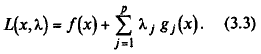
Определение 3. 2. Градиентом обобщенной (классической) функции Лагранжа по х называется вектор-столбец, составленный из ее частных производных первого порядка по x_i, i = 1, …, n:

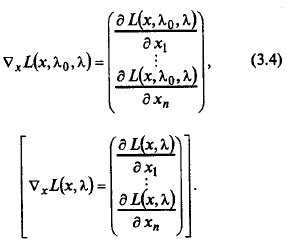
Определение 3. 3. Вторым дифференциалом обобщенной (классической) функции Лагранжа L (x, λ₀, λ) [ L (x, λ)] называется функция

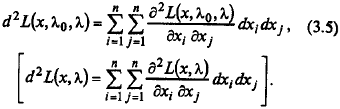
Определение 3. 4. Первым дифференциалом ограничения g_j (x) называется функция

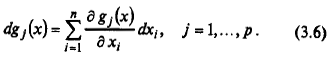
Пример 3.1. Выписать функции (3.2) – (3.6) для задачи поиска условного экстремума функции 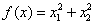на множестве X = { x | x ₂ ² – x ₁ + 3 = 0}, заданном ограничением g ₁ (x) = x ₂ ² – x ₁ + 3 = 0.

Обобщенная функция Лагранжа: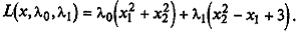

Классическая функция Лагранжа: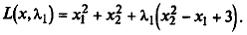

Градиент функций Лагранжа:

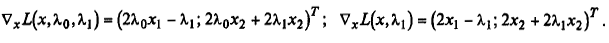
Второй дифференциал функций Лагранжа:

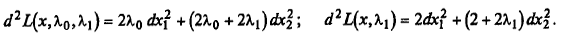
Первый дифференциал ограничения: dg ₁ (x) = – dx ₁ + 2 x ₂ dx ₂.

Определение 3.5. Ограничение g_j (x) ≤ 0 называется активным в точке х *, если g_j (x *) = 0. Если g_j (x *) < 0, то ограничение называется пассивным.

Определение 3. 6. Градиенты ограничений g ₁ (x), …, g_m (x) являются линейно независимыми в точке х *, если равенство 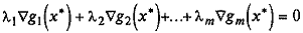выполняется только при λ₁ = λ₂ = … = λ _т = 0. Если существуют числа λ₁, …, λ _т одновременно не равные нулю, для которых равенство выполняется, то градиенты линейно зависимы. В этом случае один из них есть линейная комбинация остальных. Один вектор ∇ g ₁ (x *) тоже образует систему векторов: при ∇ g ₁ (x *) ≠ 0 линейно независимую, а при ∇ g ₁ (x *) = 0 линейно зависимую.

Система векторов, содержащая нулевой вектор, всегда линейно зависима. Если 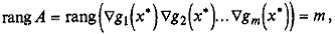то системавекторов линейно независима. Если rang А < т, то система линейно зависима.