Теория электромагнитного поля основана на системе уравнений Максвелла. В областях, где среда однородна и изотропна, и при отсутствии сторонних источников уравнения Максвелла принимают вид:
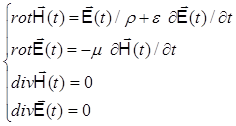
Здесь 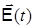 и
и 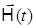 - напряженности электрического и магнитного полей,
- напряженности электрического и магнитного полей, 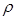 ,
, 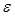 и
и 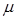 -свойства среды (сопротивление, диэлектрическая и магнитная проницаемости).
-свойства среды (сопротивление, диэлектрическая и магнитная проницаемости).
Обычно в структурной электроразведке рассматриваются немагнитные горные породы, для которых 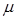 равна
равна 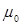 - магнитной проницаемости вакуума.
- магнитной проницаемости вакуума.
В квазистационарном приближении токами смещения (вторым членом в правой части первого уравнения Максвелла) пренебрегают по отношению к токам проводимости (первому члену). Тогда первое уравнение Максвелла записывается следующим образом:
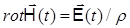
При рассмотрении гармонических полей в электроразведке применяется символический метод, заключающийся в представлении векторов, описывающих поле, в виде 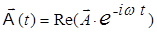 , где
, где 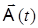 - сам вектор,
- сам вектор, 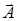 - его комплексная амплитуда,
- его комплексная амплитуда, 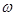 - круговая частота,
- круговая частота, 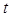 - время. Для комплексных амплитуд электрического
- время. Для комплексных амплитуд электрического 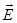 и магнитного
и магнитного 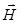 полей уравнения Максвелла принимают вид:
полей уравнения Максвелла принимают вид:
|
|
|
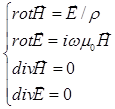
Переходя к координатной записи первого уравнения Максвелле, получим:
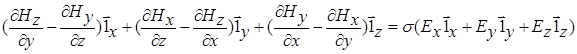
Поскольку в нашей модели поле и разрез не меняются по горизонтали, все горизон-тальные производные в этом уравнении равны нулю и оно может быть упрощено:
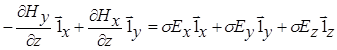 (2.1)
(2.1)
Второе уравнение Максвелла в координатной записи принимает вид:
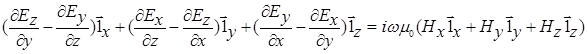
Аналогичным образом это уравнение может быть упрощено:
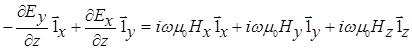 (2.2)
(2.2)
Вычленяя из уравнений (2.1) и (2.2) составляющие при 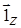 , получим, что
, получим, что  и
и 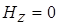 . Таким образом, вертикальные компоненты электрического и магнитного полей в модели Тихонова - Каньяра отсутствуют.
. Таким образом, вертикальные компоненты электрического и магнитного полей в модели Тихонова - Каньяра отсутствуют.
Теперь вычленим из уравнения (2.1) составляющие при 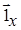 , а из уравнения (2.2) - составляющие при
, а из уравнения (2.2) - составляющие при 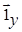 и запишем полученные уравнения в одну систему:
и запишем полученные уравнения в одну систему:
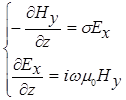 (2.3)
(2.3)
В другую систему включим уравнения, возникающие при вычленении из уравнения (2.1) составляющих при  , а из уравнения (2.2) - составляющих при
, а из уравнения (2.2) - составляющих при 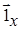 :
:
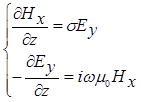 (2.4)
(2.4)
Независимость систем (2.3) и (2.4) свидетельствует о том, что МТ-поле в модели Тихонова - Каньяра состоит из двух независимых частей, называемых модами. Первая мода содержит компоненты 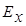 и
и 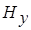 , а вторая - компоненты
, а вторая - компоненты 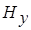 и
и 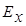 .
.
Выражая 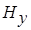 из второго уравнения системы (2.3) и подставляя в первое, получим одномерное уравнение Гельмгольца для компоненты
из второго уравнения системы (2.3) и подставляя в первое, получим одномерное уравнение Гельмгольца для компоненты 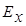 :
:
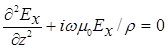
Аналогичным образом выражая 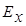 из первого уравнения этой системы и подставляя во второе, получим одномерное уравнение Гельмгольца для
из первого уравнения этой системы и подставляя во второе, получим одномерное уравнение Гельмгольца для 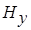 :
:
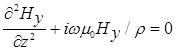
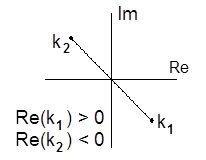 Рис. 2. К вопросу о выборе
Рис. 2. К вопросу о выборе 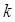 . .
|
Введем волновое число 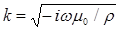 . Поскольку квадратный корень из комплексного числа представляет собой двузначную функцию, будем брать то значение
. Поскольку квадратный корень из комплексного числа представляет собой двузначную функцию, будем брать то значение 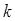 , реальная часть которого положительна (рис. 2). Действительная и мнимая части волнового числа могут быть записаны в виде:
, реальная часть которого положительна (рис. 2). Действительная и мнимая части волнового числа могут быть записаны в виде:
|
|
|
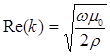
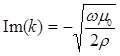
Теперь одномерные уравнения Гельмгольца для 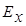 и
и 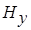 примут вид:
примут вид:
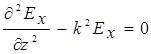
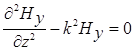 (2.5)
(2.5)
Полученные уравнения и являются исходными при решении прямой задачи МТЗ. Они описывают поведение поля внутри слоя, имеющего сопротивление 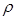 .
.
Отметим, что такая же система уравнений может быть получена для моды, содержащей компоненты 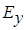 и
и 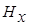 путем преобразований системы (2.4). Таким образом, в модели Тихонова - Каньяра обе моды равнозначны. Поэтому в дальнейшем мы будем оперировать лишь модой, содержащей
путем преобразований системы (2.4). Таким образом, в модели Тихонова - Каньяра обе моды равнозначны. Поэтому в дальнейшем мы будем оперировать лишь модой, содержащей 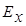 и
и 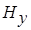 , а все выкладки для
, а все выкладки для 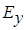 и
и 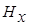 могут быть получены совершенно аналогичным способом.
могут быть получены совершенно аналогичным способом.
На границах слоев выполняются условия сопряжения, которые заключаются в том, что компоненты 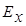 ,
, 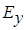 ,
, 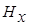 и
и 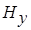 непрерывны при переходе от одного слоя к другому.
непрерывны при переходе от одного слоя к другому.
 2015-06-28
2015-06-28 616
616








