Прямая линия на плоскости.
Различные уравнения прямой на плоскости.
Определение. Уравнение прямой – это уравнение, связывающее координаты
 |
x и y любой точки, лежащей на прямой.
Уравнение прямой с угловым коэффициентом.
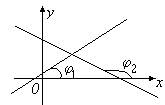
Определение. Угловым коэффициентом прямой называется тангенс угла наклона этой прямой к оси ОХ.
Угловой коэффициент обозначается через k.
Итак, 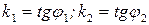
Итак, угловой коэффициент обозначается 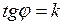 .
.
Если j- острый угол, то k >0, если j- тупой угол, то k< 0, если j=0 прямая параллельна оси ОХ и k= 0, если 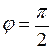 , то прямая не имеет углового коэффициента.
, то прямая не имеет углового коэффициента.
Напишем уравнение прямой, имеющей угловой коэффициент, равный k и отсекающей отрезок величины b на оси OY.
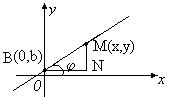
Пусть M(x,y)- произвольная точка прямой.
Рассмотрим треугольник MBN; он прямоугольный. Очевидно, что 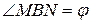
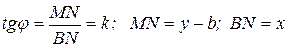
Значит 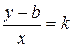 , откуда получаем уравнение
, откуда получаем уравнение 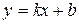 (1)
(1)
Это и есть уравнение прямой с угловым коэффициентом.
2. Уравнение прямой, проходящей через данную точку в данном направлении.
Дана точка 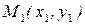 , k – угловой коэффициент. Написать уравнение прямой, проходящей через точку
, k – угловой коэффициент. Написать уравнение прямой, проходящей через точку 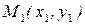 и имеющей угловой коэффициент k.
и имеющей угловой коэффициент k.
|
|
|
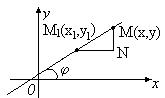
Пусть M(x,y) – произвольная точка прямой.
Рассмотрим треугольник M1MN:
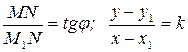
Откуда получаем искомое уравнение: 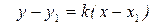 (2)
(2)
3. Уравнение прямой, проходящей через 2 точки.
Пусть даны две точки 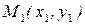 и
и 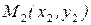 . Написать уравнение прямой, проходящей через эти точки.
. Написать уравнение прямой, проходящей через эти точки.
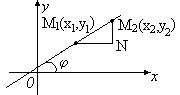
Угловой коэффициент k определим из треугольника M2M1N:
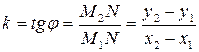
Подставим полученное значение k в уравнение (2):
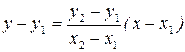
Разделим обе части уравнения на 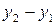 :
:
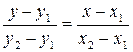
Запишем полученное уравнение в виде:
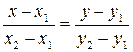 (3)
(3)
Это и есть искомое уравнение прямой, проходящей через две точки.
4. Общее уравнение прямой.
Уравнение вида Ax+By+C=0 (4) называется общим уравнением прямой.
а). Пусть 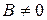 , тогда это уравнение можно записать в виде:
, тогда это уравнение можно записать в виде:
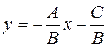
Это и есть уравнение прямой с угловым коэффициентом, т.е. уравнение
вида 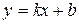 (1), где
(1), где 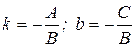
Так как уравнение (1) есть уравнение прямой, то и уравнение (4) есть также уравнение прямой.
б). Если В=0, мы получаем 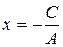 . Это есть уравнение прямой, параллельной оси ОУ.
. Это есть уравнение прямой, параллельной оси ОУ.
Рассмотрим примеры.
1). Написать уравнение прямой, проходящей через точку 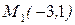 и образующей угол
и образующей угол 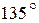 с положительным направлением оси ОХ.
с положительным направлением оси ОХ.
Решение. Найдем угловой коэффициент искомой прямой:
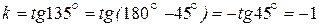
Тогда искомое уравнение примет вид 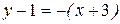
или 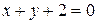
2). Написать уравнение прямой, проходящей через две точки: 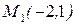 и
и 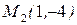
Решение. Искомое уравнение будет 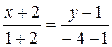
или 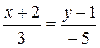
3). Найти угловой коэффициент прямой 5x-3y+6=0.
Решение. Запишем уравнение прямой в виде уравнения прямой с угловым коэффициентом:
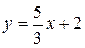
откуда 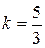
5. Уравнение прямой, проходящей через данную точку, перпендикулярно данному вектору.
Дана точка 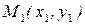 и вектор
и вектор 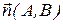 . Написать уравнение прямой, проходящей через точку
. Написать уравнение прямой, проходящей через точку 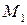 , перпендикулярно вектору
, перпендикулярно вектору 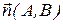 .
.
|
|
|
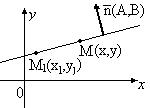
Пусть 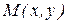 - произвольная точка прямой.
- произвольная точка прямой.
Очевидно, что векторы 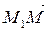 и
и 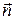 перпендикулярны:
перпендикулярны: 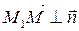 .
.
Условие перпендикулярности двух векторов – это равенство нулю их скалярного произведения:
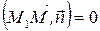
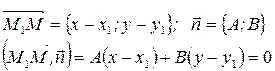
Итак, получаем уравнение 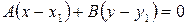 (5)
(5)
Уравнение (5) можно записать в виде Ax+By+C=0,
где 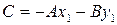
Таким образом, коэффициенты А и В в общем уравнении прямой являются координатами вектора, перпендикулярного к этой прямой. Вектор 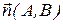 называется нормальным вектором прямой.
называется нормальным вектором прямой.
Пример. Написать уравнение прямой, проходящей через точку 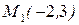 , перпендикулярно вектору
, перпендикулярно вектору 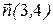 .
.
Решение. Используем уравнение (5) 3(x+2)+4(y-3)=0
Окончательно, 3x+4y-6=0
6. Уравнение прямой в отрезках на осях.
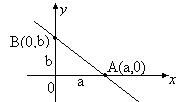 Пусть требуется написать уравнение прямой, отсекающей на координатных осях ОХ и ОУ отрезки величин a и b соответственно.
Пусть требуется написать уравнение прямой, отсекающей на координатных осях ОХ и ОУ отрезки величин a и b соответственно.
Заданная прямая проходит через две точки A(a,0) и B(0,b). Используем уравнение прямой, проходящей через две точки:
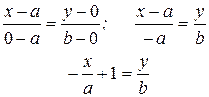
Окончательно, получаем 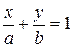 (6)
(6)
Пример. Дана прямая 2x-3y-6=0. Привести это уравнение к уравнению в отрезках на осях.
Чтобы получить отрезок a, отсекаемый на оси ОХ, нужно положить в данном уравнении y=0; чтобы получить отрезок b – х=0.
y=0; 2x-6=0; 2x=6; x=3; т.е. a=3
x=0; -3y-6=0; -3y=6; y=-2; т.е. b=-2
Искомое уравнение примет вид:
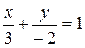
7. Нормальное уравнение прямой.
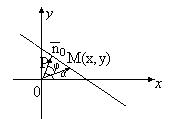
Пусть известно расстояние р от прямой до начала координат, и угол α, образуемый перпендикуляром к прямой и положительным направлением оси ОХ. Требуется написать уравнение прямой.
Пусть 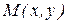 - произвольная точка прямой,
- произвольная точка прямой, 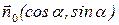 - единичный нормальный вектор прямой.
- единичный нормальный вектор прямой.
Найдем скалярное произведение 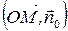 .
.
По определению скалярного произведения:
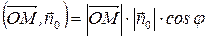 ,
,
где 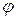 - угол между векторами
- угол между векторами 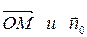 .
.
Но 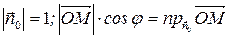
Следовательно, мы получим 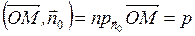
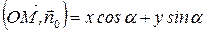
Итак, мы получаем уравнение 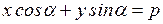 или, окончательно,
или, окончательно,
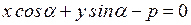 (7).
(7).
 2015-06-28
2015-06-28 16467
16467
