Замечательный польский ученый Збигнев Огжевальский из некоторых представлений общей теории и совокупности уравнений (410) и (411) получил известные соотношение Гейзенберга и уравнения Клейна-Гордона, Дирака и Шредингера, составляющие основу квантовой механики. Огжевальский ввел в формулы (410) и (411) понятие плотности электромагнитной энергии [16]
r = r(х; у; z; t) = f(eЕ2 + mН2), (416)
где
`e = e(r); m = m(r); `D =`Е e(r); `В =`Н m(r).
Здесь использованы принятые в электродинамике обозначения электрической (e, Е, D) и магнитной (m, Н, В) проницаемости, напряженности и индукции.
Соотношение Гейзенберга Огжевальский получает при условии, что функция (416) выбирается в соответствии с кривой ошибок Гаусса. При этом элементарная частица Огжевальского описывается с помощью уравнений обычного волнового пакета.
Посредством функции (416) Огжевальский из формул (410) и (411) нашел нелинейные уравнения, которые в интегральной форме имеют вид
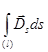 =
= 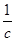
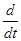
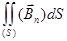 ; (417)
; (417)
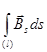 =
= 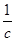
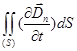 ; (417)
; (417)
Эти уравнения описывают вихревые и соленоидальные поля. Проницаемости e и m характеризуют скалярное поле U (x; y; z), векторы `Е, `Н, `D и `В – векторное поле`V (x; y; z). При r = const уравнения (417) переходят в обычные линейные уравнения Максвелла. На основе соотношения (417) Огжевальский приходит к выводу о том, что элементарные частицы имеют форму тороида с радиусами R и r.
|
|
|
Применение теоремы Стокса к уравнениям (417) дает
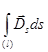 =
= 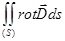 =
= 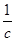
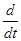
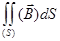 ; (418)
; (418)
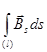 =
= 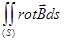 =
= 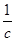
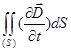 , (418)
, (418)
откуда
rot 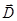 = - (1/c)(¶
= - (1/c)(¶ 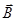 /¶t); rot
/¶t); rot 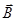 = - (1/c)(¶
= - (1/c)(¶ 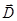 /¶t), (419)
/¶t), (419)
где
` D =`Е e(r); ` В =`Н m(r). (420)
Известно, что
rot(U 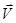 ) = Urot
) = Urot 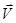 + gradU x
+ gradU x 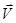 ; (421)
; (421)
В результате из выражений (419) получается
e(r)rot 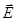 = - (1/c)m(r)
= - (1/c)m(r) 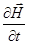 - grade(r)
- grade(r) 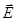 - (1/c)
- (1/c) 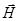
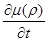 ; (422)
; (422)
m(r)rot 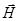 = (1/c)e(r)
= (1/c)e(r) 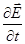 - gradm(r)
- gradm(r) 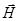 + (1/c)
+ (1/c) 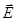
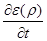 ; (422)
; (422)
Любое векторное поле `V, достаточно быстро убывающее при удалении в бесконечность, можно разложить на сумму безвихревого `V1 и соленоидального `V2 полей. Тогда соотношение (422) приводит к уравнениям
e(r)rot 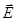 = - (1/c)m(r)
= - (1/c)m(r) 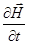 - С1; (423)
- С1; (423)
m(r)rot 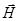 = (1/c)e(r)
= (1/c)e(r) 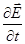 - С2; (423)
- С2; (423)
div 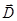 = 0; div
= 0; div 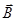 = 0; (424)
= 0; (424)
grade(r) 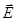 = С2; gradm(r)
= С2; gradm(r) 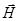 = С1; (425)
= С1; (425)
(1/c) 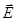
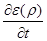 = 0; - (1/c)
= 0; - (1/c) 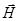
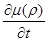 =0. (426)
=0. (426)
При С1 = С2 = 0 уравнения (423) и (424) описывают внутреннее вихревое поле тороидальной элементарной частицы, уравнения (425) – ее внешнее безвихревое поле, уравнения (426) – поведение частицы во времени.
Из соотношений (423) – (426) формально выводятся все основные уравнения квантовой механики. Для этого уравнения (423) – (426) надо линеаризовать, разложив функцию r в степенной ряд и ограничившись первым слагаемым ряда, после чего
r @ r0 = const. (427)
Благодаря этому формулы (423) приобретают вид равенств (419), имеющих с учетом разложения (427) смысл линейных уравнений Максвелла. При этом равенства (419) можно переписать следующим образом:
Ñ2 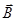 - (1/c2)
- (1/c2) 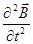 = 0; Ñ2
= 0; Ñ2 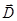 - (1/c2)
- (1/c2) 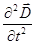 = 0.
= 0.
или (уравнение Даламбера)
[Ñ2 - (1/c2) 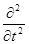 ]j = 0. (428)
]j = 0. (428)
разделив это уравнение на с2 и приняв во внимание, что с2 = wgwf, где wg и wf - групповая и фазовая скорости тороидальной частицы соответственно, получим
|
|
|
[(wg/wf)Ñ2 - (1/wf2) 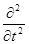 ]j = 0. (429)
]j = 0. (429)
Это выражение Огжевальский называет геометрическим уравнением Клейна-Гордона.
В квантовой механике пользуются плоской волной для которой wg = wf, или точечной частицей, для которой R = r = 0. Тогда уравнение (429) приобретает вид
[Ñ2 - (1/c2) 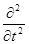 - k02]j = 0. (430)
- k02]j = 0. (430)
где в (430)
k0 = 2pсm0/h.
Это и есть обычное уравнение Клейна-Гордона.
Как известно, Дирак расчленил релятивистское уравнение второй степени Клейна-Гордона на уравнения первой степени. Огжевальский пользуется тем же приемом. Выражение (429) он переписывает следующим образом:
- (1/c2) 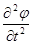 = - (wg/wf)Ñ2j + 4p2с2m02/h2,
= - (wg/wf)Ñ2j + 4p2с2m02/h2,
откуда после несложных преобразований получается
- (1/c2) 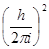
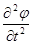 = -
= - 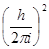 (wg/wf)Ñ2j + m02/h2.
(wg/wf)Ñ2j + m02/h2.
Введение сюда операторов
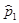 =
= 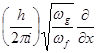 ;
; 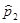 =
= 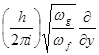 ;
;
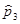 =
= 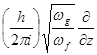 ;
; 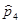 =
= 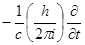 .
.
дает
(ch/2pi)(wg/wf)[a1(¶Y/¶x) + a2(¶Y/¶y) + a3(¶Y/¶z)] + a4 m02c2Y = - (h/2pi) (¶Y/¶t). (431)
Это выражение Огжевальский именует геометрическим уравнением Дирака. Оно превращается в обычное уравнение Дирака при wg = wf.
В нерелятивистском случае уравнение Дирака (431) переходит в уравнение Шредингера, которое в геометрической форме записывается следующим образом:
 |
Ñ2Y + (2m/
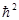 )(E + e2/ÖR2(z) + z2)Y = 0, (432)
)(E + e2/ÖR2(z) + z2)Y = 0, (432)
где
 |
ÖR2(z) + z2 = r, (433)
r - радиус Бора;
R(z) - большой радиус тороидальной частицы;
z - расстояние тороидального электрона от атомного ядра.
С помощью нелинейных уравнений электродинамики и тороидальной модели элементарных частиц Огжевальский объяснил многие непонятные прежде экспериментальные факты и предсказал ряд новых явлений. В частности, он дал непротиворечивое с точки зрения квантовой и классической электродинамики описание движения электрона в атоме водорода, раскрыл единую природу так называемых электромагнитных, слабых и сильных взаимодействий, устранил из квантовой механики знаменитые бесконечности, связанные с расчетом энергии и массы, дал простую и естественную интерпретацию волновой функции и т.д.
Как видим, все понятия квантовой механики вытекают из общей теории при определенных весьма существенных допущениях и упрощениях. На примере уравнений Максвелла и Огжевальского легко почувствовать трудности, которые связаны с выводом достаточно универсальных уравнений, одновременно охватывающих несколько количественных уровней мироздания с учетом их взаимного влияния, а также убедиться в том, что на сегодняшний день наши успехи в этом деле более чем скромны. Применение идей общей теории значительно облегчает решение поставленной задачи.
 2015-06-28
2015-06-28 518
518








