Координатное представление векторов

Координаты вектора — это числа х ₁, х ₂, х ₃,..., являющиеся коэффициентами ЛК:

х = х ₁ е₁ + х ₂ е₂ + х ₃ е₃ +....,

где е₁, е₂, е₃,... — базисные векторы (базис).

Координаты векторов принято записывать двумя альтернативными способами:

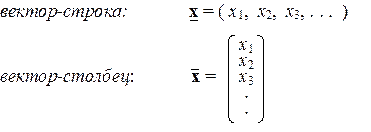
Подчеркнем, что вектор-столбец принято отмечать чертой над символом вектора, а вектор-строку — чертой под символом вектора. Вектор-столбцы часто называют контравариантными векторами (контра -векторами), а вектор-строки — ковариантными векторами (ко -векторами). С математической точки зрения контра- и ковекторы полностью эквивалентны, однако они могут использоваться для обозначения различных типов физических объектов.

Важную роль играет следующее обстоятельство: выбор базиса неоднозначен и в любом ЛП возможных базисов бесконечно много, однако все они содержат одно и то же число базисных векторов. Это фундаментальное число называется размерностью ЛП.

Координатное представление позволяет очень просто и наглядно выполнять операции над векторами.

При сложении двух векторов складываются их координаты, расположенные на одинаковых позициях. При умножении вектора на число все его координаты умножаются на это число.

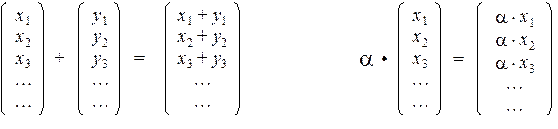
Если мы имеем линейную комбинацию, то любая координата результирующего вектора будет получаться как линейная комбинация координат исходных векторов, расположенных на соответствующих позициях.

Наконец отметим, что координатное представление базисных векторов имеет особенно простой вид: каждый базисный вектор имеет одну координату (под номером, совпадающим с номером данного базисного вектора), равную единице, а все остальные его координаты равны нулю:

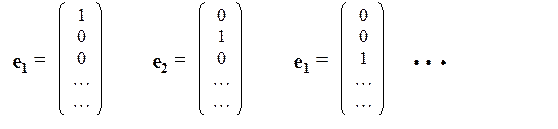
Используя координатное представление, можно ввести еще одну операцию, которая выполняется над парой векторов. Эта операция называется скалярным умножением векторов и изображается одним из следующих способов:

a = (x, y) = x · y = á x | y ñ

Сомножитель, идущий первым, всегда представляет собой ко -вектор (вектор-строку), тогда как второй сомножитель всегда является контра -вектором (вектор-столбцом). Результатом этой операции является число, называемое скалярным произведением векторов, значение которого можно рассчитать через координаты векторов х и у по формуле:

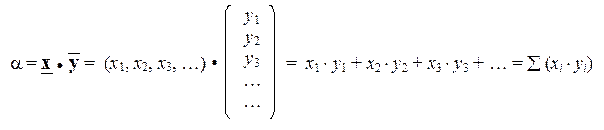
Аналогичным образом можно найти и скалярный квадрат вектора, т.е. произведение вектора "на себя":

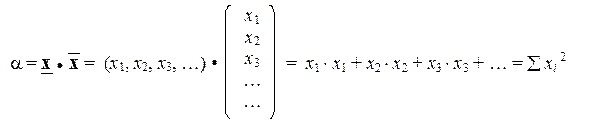
Скалярный квадрат вектора называют также квадратом модуля вектора, поскольку корень квадратный из произведения вектора на себя называется модулем вектора

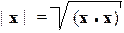
С помощью скалярного умножения можно ввести метрические понятия в модель ЛВП, т.е. определить длины векторов и углы между ними. В качестве длины вектора принимается величина его модуля. Угол между двумя векторами (j) определяется по формуле:

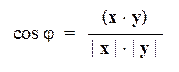
Отметим следующее обстоятельство: при умножении вектора на некоторое число a его модуль (длина) увеличивается в a раз, тогда как ориентация (углы относительно всех остальных векторов) остается неизменной. Таким образом, среди всех векторов мы можем выделить такие их подмножества, в которые входят все векторы одной и той же ориентации, но отличающиеся друг от друга длиной. Такие подмножества сами по себе образуют ЛП с размерностью 1 и называются обычно лучами. В каждом луче можно выделить один особый вектор, длина которого равна единице. Такой вектор служит представителем данного луча и называется нормированным.

Любой другой вектор можно получить из нормированного посредством умножения на некоторое число или свести к нормированному посредством операции, называемой нормировкой (нормированием). При нормировке каждая координата вектора делится на величину модуля этого вектора. Например, трехмерный вектор х = (3, 5, 8) имеет длину:

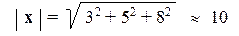
и, следовательно, является ненормированным. Для нормировки разделим все координаты на 10 и получим нормированный вектор

х' = (3/10, 5/10, 8/10)

совпадающий по направлению с исходным (т.е. принадлежащий тому же лучу), но уже имеющий единичную длину.