2015-06-28
496
Выражение вида
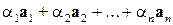
называется линейной комбинацией векторов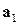 
, 
,..., 
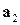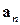. Числа 
, 
, …, 
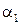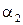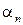называются ее коэффициентами.
Если вектор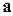 
равен линейной комбинации векторов 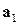, ,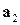..., , 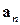то говорят, что вектор 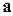линейно выражается через векторы , , …, .
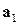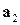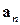Система векторов 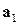, ,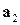..., 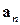называется линейно зависимой, если существуют числа 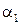, , 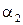…, , 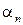не все равные нулю такие, что
.
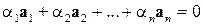В противном случае система векторов называется линейно независимой.
Предложение 1.1. Система векторов, содержащая не менее двух векторов, линейно зависима тогда и только тогда, когда какой-нибудь вектор этой системы представим в виде линейной комбинации остальных.
Доказательство. Пусть система векторов 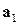, , 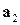…, 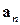линейно зависима. В соответствии с определением существуют числа 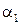, , 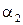…, , 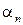не все равные нулю такие, что 
.
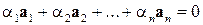Пусть, например,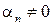 
. Тогда
,
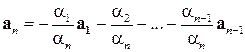т.е. вектор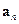 
представлен в виде линейной комбинации векторов , , …, .
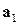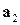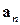Обратно, пусть какой-нибудь вектор, например 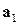, представим в виде линейной комбинации остальных:
.
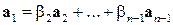Отсюда
.
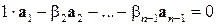Так как коэффициент при 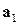здесь не равен нулю, то векторы линейно зависимы.
Замечание 1.1. Понятие линейной зависимости является алгебраическим. Геометрические его выражения – коллинеарность в двумерном случае и компланарность – в трехмерном.
Предложение 1.2. Если при добавлении вектора 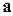к линейно независимой системе 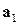, , 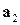…, 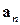получаем линейно зависимую систему, то вектор 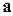линейно выражается через векторы , , …, .
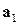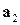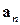Доказательство. Найдутся такие числа , , …, ,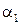 
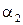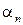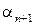, не все равные нулю, что
. 
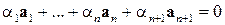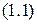
Тогда именно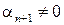 
. Действительно, если 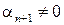, то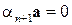 
и, следовательно, равенство 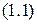превращается в равенство
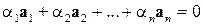
и среди чисел 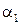, , 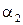…, , 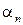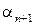найдется отличное от нуля. Тогда система 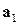, , 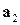…, 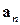линейно зависима. Противоречие.
Следовательно, 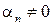и из 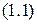получаем
.
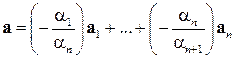Предложение доказано.
