Закон больших чисел в форме Чебышева

Если явление устойчивости средних имеет место в действительности, то в математической модели, с помощью которой мы изучаем случайные явления, должна существовать отражающая этот факт теорема.
В условиях этой теоремы введем ограничения на случайные величины X ₁, X ₂, …, X_n:

а) каждая случайная величина Х_i имеет математическое ожидание

M (Х_i) = a;

б) дисперсия каждой случайной величины конечна или, можно сказать, что дисперсии ограничены сверху одним и тем же числом, например С, т. е.

D (Х_i) < C, i = 1, 2, …, n;

в) случайные величины попарно независимы, т. е. любые две X_i и X_j при i ¹ j независимы.

Тогда, очевидно

D (X ₁ + X ₂ + … + X_n)= D (X ₁) + D (X ₂) +... + D (X_n).

Сформулируем закон больших чисел в форме Чебышева.

Теорема Чебышева: при неограниченном увеличении числа n независимых испытаний «средняя арифметическая наблюдаемых значений случайной величины сходится по вероятности к ее математическому ожиданию», т. е. для любого положительного ε

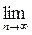Р (| – а| < ε) = 1. (4.1.1)

Смысл выражения «средняя арифметическая = 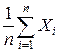сходится по вероятности к a» состоит в том, что вероятность того, что будет сколь угодно мало отличаться от a, неограниченно приближается к 1 с ростом числа n.

Доказательство. Для конечного числа n независимых испытаний применим неравенство Чебышева для случайной величины = :

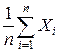Р (| – M () | < ε) ≥ 1 – 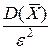. (4.1.2)

Учитывая ограничения а – в, вычислим M () и D ():

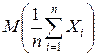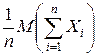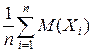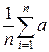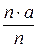M () = = = = = = а;

D () = = = = = = .

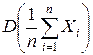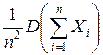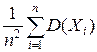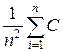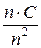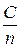Подставляя M () и D () в неравенство (4.1.2), получим

Р (| – а| < ε)≥1 – .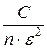

Если в неравенстве (4.1.2) взять сколь угодно малое ε >0и n ® ¥, то получим

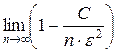= 1,

что и доказывает теорему Чебышева.

Из рассмотренной теоремы вытекает важный практический вывод: неизвестное нам значение математического ожидания случайной величины мы вправе заменить средним арифметическим значением, полученным по достаточно большому числу опытов. При этом, чем больше опытов для вычисления, тем с большей вероятностью (надежностью) можно ожидать, что связанная с этой заменой ошибка ( – а)не превзойдет заданную величину ε.

Кроме того, можно решать другие практические задачи. Например, по значениям вероятности (надежности) Р = Р (| – а| < ε)и максимальной допустимой ошибке ε определить необходимое число опытов n; по Р и п определить ε; по ε и п определить границу вероятности события | – а | < ε.

Частный случай. Пусть при n испытаниях наблюдаются n значений случайной величины X, имеющей математическое ожидание M (X) и дисперсию D (X). Полученные значения можно рассматривать как случайные величины Х ₁, Х ₂, Х ₃, ..., Х_n,. Это следует понимать так: серия из п испытаний проводится неоднократно, поэтому в результате i -го испытания, i = l, 2, 3,..., п, в каждой серии испытаний появится то или иное значение случайной величины X, не известное заранее. Следовательно, i -e значение x_i случайной величины, полученное в i -м испытании, изменяется случайным образом, если переходить от одной серии испытаний к другой. Таким образом, каждое значение x_i можно считать случайной величиной X_i .

Предположим, что испытания удовлетворяют следующим требованиям:

1. Испытания независимы. Это означает, что результаты Х ₁, Х ₂,
Х ₃,..., Х_n испытаний – независимые случайные величины.

2. Испытания проводятся в одинаковых условиях – это означает, с точки зрения теории вероятностей, что каждая из случайных величин Х ₁, Х ₂, Х ₃, ..., Х_n имеет такой же закон распределения, что и исходная величина X, поэтому M (X_i) = M (X)и D (X_i) = D (X), i = 1, 2,.... п.

Учитывая вышеуказанные условия, получим

Р (| – а| < ε)≥1 – 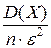. (4.1.3)

Пример 4.1.1. Дисперсия случайной величины X равна 4. Сколько требуется произвести независимых опытов, чтобы с вероятностью не менее 0,9 можно было ожидать, что среднее арифметическое значение этой случайной величины будет отличаться от математического ожидания менее чем на 0,5?

Решение. По условию задачи ε = 0,5; Р (| – а|< 0,5) ≥ 0,9. Применив формулу (4.1.3) для случайной величины Х, получим

P (| – M (X) | < ε) ≥ 1 – .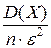

Из соотношения

1 – 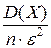= 0,9

определим

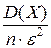= 0,1;

п = 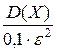= = 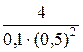160.

Ответ: требуется произвести 160 независимых опытов.

Если предположить, что средняя арифметическая распределена нормально, то получаем:

Р (| – а| < ε) = 2 Φ (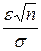) ≥ 0,9.

Откуда, воспользовавшись таблицей функции Лапласа, получим ≥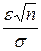
≥ 1,645, или 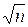≥ 6,58, т. е. n ≥49.

Пример4.1.2. Дисперсия случайной величины Х равна D(Х) = 5. Произведено 100 независимых опытов, по которым вычислено . Вместо неизвестного значения математического ожидания а принята . Определить максимальную величину ошибки, допускаемую при этом с вероятностью не менее 0,8.

Решение. По условию задачи n = 100, Р (| – а| < ε) ≥0,8. Применим формулу (4.1.3)

Р (| – а| < ε) ≥1 – .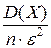

Из соотношения

1 – 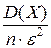= 0,8

определим ε:

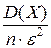= 0,2;

ε ² = 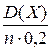= = 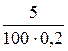0,25.

Следовательно, ε = 0,5.

Ответ: максимальная величина ошибки ε = 0,5.

4.2. Закон больших чисел в форме Бернулли [4]

Хотя в основе любого статистического вывода лежит понятие вероятности, мы лишь в немногих случаях можем определить вероятность события непосредственно. Иногда эту вероятность можно установить из соображений симметрии, равной возможности и т.п., но универсального метода, который позволял бы для произвольного события указать его вероятность, не существует. Теорема Бернулли дает возможность приближенной оценки вероятности, если для интересующего нас события А можно проводить повторные независимые испытания. Пусть произведено п независимых испытаний, в каждом из которых вероятность появления некоторого события А постоянна и равна р.

Теорема Бернулли. При неограниченном возрастании числа независимых испытаний п относительная частота 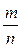появления события А сходится по вероятности к вероятности p появления события А,т. е.

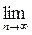P (½ 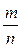- p ½≤ ε) = 1, (4.2.1)

где ε – сколь угодно малое положительное число.

Для конечного n при условии, что 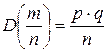, неравенство Чебышева для случайной величины 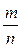будет иметь вид:

P (| 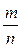– p| < ε) ≥ 1 – 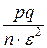.(4.2.2)

Доказательство. Применим теорему Чебышева. Пусть X_i – число появлений события А в i -ом испытании, i = 1, 2,..., n. Каждая из величин X_i может принять лишь два значения:

X_i = 1 (событие А наступило) с вероятностью p,

X_i = 0 (событие А не наступило) с вероятностью q = 1 – p.

Пусть Y_n = 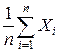. Сумма X ₁ + X ₂ + … + X_n равна числу m появлений события А в n испытаниях (0 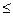m 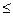n), а, значит, Y_n = 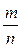– относительная частота появления события А в n испытаниях. Математическое ожидание и дисперсия X_i равны соответственно:

M (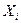) = 1∙ p + 0∙ q = p,

D (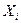) = M (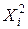) – M (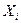)² = 1²∙ p + 0²∙ q – p ² = p – p ² = = p (1 – p) = pq.

Тогда

M (Y_n) = 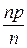= p; D (Y_n) = 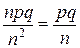® 0.

Следовательно, выполняются условия теоремы Чебышева, т. е. 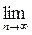P (½ 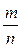- p ½≤ ε) = 1, что и требовалось доказать.

Из теоремы Бернулли следует, что при достаточно большом числе испытаний относительная частота 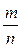появления события практически утрачивает свой случайный характер, приближаясь к постоянной величине p – вероятности данного события. В этом и состоит принцип практической уверенности.

Пример 4.2.1. С целью установления доли брака продукции было проверено по схеме возвратной выборки 1000 единиц. Какова вероятность того, что установленная этой выборкой доля брака по абсолютной величине будет отличаться от доли брака по всей партии не более чем на 0,01, если известно, что в среднем на каждые 10000 изделий приходится 500 бракованных?

Решение. По условию задачи число независимых испытаний n = 1000;

p = 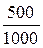= 0,05; q = 1 – p = 0,95; ε = 0,01.

Применяя формулу (4.2.2), получим

P (| 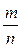– p| < 0,01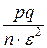) ≥ 1 – = 1 – 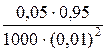= 0,527.

Ответ: с вероятностью не менее 0,527 можно ожидать, что выборочная доля брака (относительная частота появления брака) будет отличаться от доли брака во всей продукции (от вероятности брака) не более чем на 0,01.

Пример 4.2.2. При штамповке деталей вероятность брака составляет 0,05. Сколько нужно проверить деталей, чтобы с вероятностью не менее 0,95 можно было ожидать, что относительная частота бракованных изделий будет отличаться от вероятности брака менее чем на 0,01?

Решение. По условию задачи р = 0,05; q = 0,95; ε = 0,01;

P (| 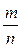– p| <0,01) ≥ 0,95.

Из равенства 1 – 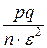= 0,95 находим n:

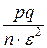= 0,05;

n = 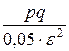= =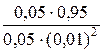9500.

Ответ: необходимо проверить 9500 деталей.

Замечание. Оценки необходимого числа наблюдений, получаемые при применении теоремы Бернулли (или Чебышева), очень преувеличены. Существуют более точные оценки, предложенные Бернштейном[5] и Хинчиным[6], но требующие более сложного математического аппарата. Чтобы избежать преувеличения оценок, иногда пользуются формулой Лапласа

P (| 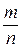– p| < ε) ≈ 2 Φ .

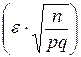Недостатком этой формулы является отсутствие оценки допускаемой погрешности.