Подгруппы группы движений плоскости

Ранее мы доказали, что множество всех движений плоскости D является группой преобразований. Эта группа называется группой движений плоскости.

Те свойства фигуры F, которые сохраняются при всех движениях, называются инвариантными свойствами этой фигуры относительно группы D или, короче, инвариантами группы D. Так, расстояние между двумя точками А и В - инвариантное свойство фигуры { А, В } относительно группы D. Это основной инвариант группы движений. Свойства фигуры быть отрезком, лучом, прямой являются примерами инвариантных свойств фигур относительно группы D. Простое отношение трех точек прямой, мера угла, площадь фигуры также является инвариантами группы D.

Рассмотрим важнейшие подгруппы группы D и укажем некоторые инварианты этих подгрупп, которые не являются инвариантами группы D.

1) Обозначим через D₁ множество всех движений первого рода. Любое движение первого рода сохраняет ориентацию плоскости. Отсюда заключаем, что если g, f Î D₁, то g× f Î D₁ и для любого движения fÎD₁ обратное движение Î D₁. Значит, D₁ - подгруппа группы D. Она называется группой движений первого рода. Любое движение первого рода сохраняет ориентацию плоскости, т.е. переводит любой репер в репер той же ориентации. Поэтому ориентация репера - инвариант группы D.

Замечание. 1) Множество D₂ движений II рода не является группой. Если f и g – движения второго рода, то g× f – движение первого рода, поэтому g× f Ï D₂.

2) Пусть D₁(М₀) – множество всех движений первого рода, для которых М₀ – неподвижная точка.

Очевидно D₁(М₀) Ì D₁. Если f, g Î D₁(М₀), то ясно, что

g×f Î D₁(М₀), и f ^-1 Î D₁(М₀). Значит D₁(М₀) - подгруппа группы D₁. Эта группа состоит из всех вращений вокруг точки М₀. Она называется группой вращений плоскости вокруг точки М₀. Расстояние от произвольной точки М до центра М₀ вращения является инвариантом группы D₁(М₀).

3) Рассмотрим множество Т, состоящее из всех параллельных переносов. Очевидно, Т Ì D₁. Пусть f и g - параллельные переносы с векторами переносов 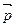и 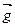. Нетрудно видеть, что если М¢ = (g×f)(М), то = + .

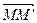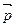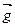Т.о., g×f - параллельный перенос, на вектор + .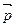

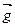Далее, т.к. преобразование М¢ = f(M) параллельный перенос, то 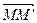= 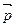. Но тогда 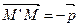, т.е. f ^-1 – параллельный перенос на вектор – 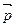. Т.о., если f, g Î Т, то g×f Î Т и f ^-1 Î Т. Этим доказано, что Т - подгруппа группы D₁; она называется группой переносов плоскости.

Определение. Две фигуры F и F¢ называются равными (или конгруэнтными), если они D - эквивалентны, т.е. если существует такое движение g, что F^¢ = g (F); пишут: F = F¢ .

Очевидно, D - эквивалентность фигур является отношением эквивалентности на множестве всех фигур плоскости и поэтому справедливы утверждения:

1) F = F для любой фигуры F.

2) F₁ = F₂ Þ F₂ = F₁.

3) (F₁ = F₂, F₂ = F₃) Þ F₁ = F₃.