Статистический ряд. Гистограмма

Пример 1. Произведено 500 измерений боковой ошибки наводки при стрельбе с самолета по наземной цели. Результаты измерений (в тысячных долях радиана) сведены в статистический ряд:

I,	—4; —3	—3; —2	-2; -1	—1; 0	0; 1	l; 2	2; 3	3; 4
* Pi	0,012	0,050	0,144	0,266	0,240	0,176	0,092	0,020

Здесь // обозначены интервалы значений ошибки наводки; mi — число наб­людений в данном интервале, р* = —- — соответствующие частоты.

При группировке наблюденных значений случайной величины по разрядам возникает вопрос о том, к какому разряду отнести значе­ние, находящееся в точности на границе двух разрядов. В этих случаях можно рекомендовать (чисто условно) считать данное зна­чение принадлежащим в равной мере к обоим разрядам и прибав­лять к числам т₁ того и другого разряда по -н-.

Число разрядов, на которые следует группировать статистический материал, не должно быть слишком большим (тогда ряд распреде­ления становится невыразительным, и частоты в нем обнаруживают незакономерные колебания); с другой стороны, оно не должно быть слишком малым (при малом числе разрядов свойства распределения описываются статистическим рядом слишком грубо). Практика пока­зывает, что в большинстве случаев рационально выбирать число разрядов порядка 10 — 20. Чем богаче и однороднее статистический материал, тем большее число разрядов можно выбирать при состав­лении статистического ряда. Длины разрядов могут быть как одина­ковыми, так и различными. Проще, разумеется, брать их одинаковы­ми. Однако при оформлении данных о случайных величинах, рас­пределенных крайне неравномерно, иногда бывает удобно выбирать в области наибольшей плотности распределения разряды более узкие, чем в области малой плотности.

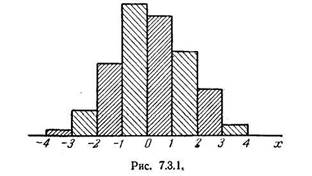
Статистический ряд часто оформляется графически в виде так называемой гистограммы. Гистограмма строится следующим обра­зом. По оси абсцисс откладываются разряды, и на каждом из раз­рядов как их основании строится прямоугольник, площадь которого равна частоте данного разряда. Для построения гистограммы нужно частоту каждого разряда разделить на его длину и полученное число взять в качестве высоты прямоугольника. В случае равных по длине

ЗАКОНЫ РАСПРЕДЕЛЕНИЯ СЛУЧАЙНЫХ ВЕЛИЧИН

[ГЛ. 7

разрядов высоты прямоугольников пропорциональны соответствующим частотам. Из способа построения гистограммы следует, что полная площадь ее равна единице.

В качестве примера можно привести гистограмму для ошибки наводки, построенную по данным статистического ряда, рассмотрен­ного в примере 1 (рис. 7.3.1).

Очевидно, при увеличении числа опытов можно выбирать все более и более мелкие разряды; при этом гистограмма будет все более приближаться к некоторой кривой, ограничивающей площадь,

равную единице. Нетрудно убедиться, что эта кривая представляет собой график плотности распределения величины X.

Пользуясь данными статистического ряда, можно приближенно построить и статистическую функцию распределения величины X. Построение точной статистической функции распределения с несколь­кими сотнями скачков во всех наблюденных значениях X слишком трудоемко и себя не оправдывает. Для практики обычно достаточно построить статистическую функцию распределения по нескольким точкам. В качестве этих точек удобне взять границы x_v x₂, • • • разрядов, которые фигурируют в статистическом ряде. Тогда, очевидно,

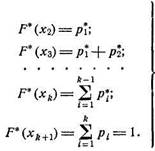
/"(*!) = 0;

(7.3.2)

140 ЗАКОНЫ РАСПРЕДЕЛЕНИЯ СЛУЧАЙНЫХ ВЕЛИЧИН [ГЛ. 7

Эту характеристику мы будем в дальнейшем называть стати­стическим средним случайной величины.

Согласно закону больших чисел, при неограниченном увеличении числа опытов статистическое среднее приближается (сходится по ве­роятности) к математическому ожиданию. При достаточно большом п статистическое среднее может быть принято приближенно равным математическому ожиданию. При ограниченном числе опытов стати­стическое среднее является случайной величиной, которая, тем не менее, связана с математическим ожиданием и может дать о нем известное представление.

Подобные статистические аналогии существуют для всех число­вых характеристик. Условимся в дальнейшем эти статистические аналогии обозначать теми же буквами, что и соответствующие чис­ловые характеристики, но снабжать их значком *.

Рассмотрим, например, дисперсию случайной величины. Она пред­ставляет собой математическое ожидание случайной величины

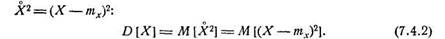
Если в этом выражении заменить математическое ожидание его статистической аналогией — средним арифметическим, мы получим статистическую дисперсию случайной величины X:

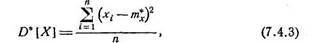
где пС_х = М* [Х\ — статистическое среднее.

Аналогично определяются статистические начальные и централь­ные моменты любых, порядков:

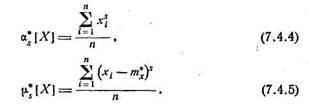
Все эти определения полностью аналогичны данным в главе 5 определениям числовых характеристик случайной величины, с той разницей, что в них везде вместо математического ожидания фигу­рирует среднее арифметическое. При увеличении числа наблюдений, очевидно, все статистические характеристики будут сходиться по вероятности к соответствующим математическим характеристикам и при достаточном п могут быть приняты приближенно равными им.

7.41

ХАРАКТЕРИСТИКИ СТАТИСТИЧЕСКОГО РАСПРЕДЕЛЕНИЯ

Нетрудно доказать, что для статистических начальных и цен­тральных моментов справедливы те же свойства, которые были выве­дены в главе 5 для математических моментов. В частности, стати­стический первый центральный момент всегда равен нулю:

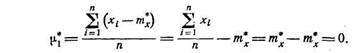
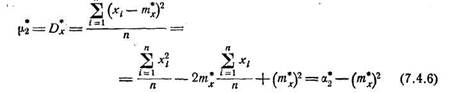
и т. д.

При очень большом количестве опытов вычисление характеристик по формулам (7.4.1) — (7.4.5) становится чрезмерно громоздким, и можно применить следующий прием: воспользоваться теми же разрядами, на которые был расклассифицирован статистический материал для построения статистического ряда или гистограммы, и считать приближенно значение случайной величины в каждом разряде постоянным и равным среднему значению, которое выступает в роли «представителя» разряда. Тогда статистические числовые характе­ристики будут выражаться приближенными формулами:

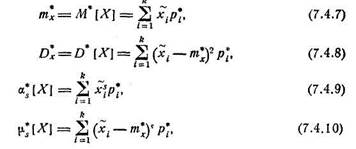
142," ЗАКОНЫ РАСПРЕДЕЛЕНИЯ СЛУЧАЙНЫХ ВЕЛИЧИН [ГЛ. 7

величины X, с той только разницей, что вместо вероятностей p_t в них стоят частоты р*, вместо математического ожидания т_х — ста­тистическое среднее т*, вместо числа возможных значений случайной величины — число разрядов.

В большинстве руководств по теории вероятностей и математической статистике при рассмотрении вопроса о статистических аналогиях для харак­теристик случайных величин применяется терминология, несколько отличная от принятой в настоящей книге, а именно, статистическое среднее именуется «выборочным средним», статистическая дисперсия—«выборочной дисперсией» и т. д. Происхождение этих терминов следующее. В статистике, особенно сельскохозяйственной и биологической, часто приходится исследовать распре­деление того или иного признака для весьма большой совокупности индиви­дуумов, образующих статистический коллектив (таким признаком может быть, например, содержание белка в зерне пшеницы, вес того же зерна, длина или вес тела какого-либо из группы животных и т. д.). Данный признак является случайной величиной, значение которой от индивидуума к индивидууму меняется. Однако, для того, чтобы составить представление о распределении этой случайной величины или о ее важнейших характери­стиках, нет необходимости обследовать каждый индивидуум дайной обширной совокупности; можно обследовать некоторую выборку достаточно боль­шого объема для того, чтобы в ней были выявлены существенные черты изучаемого распределения. Та обширная совокупность, из которой произво­дится выборка, носит в статистике название генеральной совокупности. При этом предполагается, что число членов (индивидуумов) N в генеральной совокупности весьма велико, а число членов п в выборке ограничено. При достаточно большом N оказывается, что свойства выборочных (статисти­ческих) распределений и характеристик практически не зависят от N; отсюда естественно вытекает математическая идеализация, состоящая в том, что генеральная совокупность, из которой осуществляется выбор, имеет беско­нечный объем. При этом отличают точные характеристики (закон распределе­ния, математическое ожидание, дисперсию и т. д.), относящиеся к генераль­ной совокупности, от аналогичных им «выборочных» характеристик. Выбо­рочные характеристики отличаются от соответствующих характеристик генеральной совокупности за счет ограниченности объема выборки п; при неограниченном увеличении п, естественно, все выборочные характери­стики приближаются (сходятся по вероятности) к соответствующим характе­ристикам генеральной совокупности. Часто возникает вопрос о том, каков должен быть объем выборки п для того, чтобы по выборочным характеристи­кам можно было с достаточной точностью судить о неизвестных характерис­тиках генеральной совокупности или о том, с какой степенью точности при заданном объеме выборки можно судить о характеристиках генеральной сово­купности. Такой методический прием, состоящий в параллельном рассмотрении бесконечной генеральной совокупности, из которой осуществляется выбор, и ограниченной по объему выборки, является совершенно естественным в тех областях статистики, где фактически приходится осуществлять выбор из весьма многочисленных совокупностей индивидуумов. Для практических задач, связанных с вопросами стрельбы и вооружения, гораздо <5олее характерно другое положение, когда над исследуемой случайной величиной (или системой случайных величин) производится ограниченное число оп, юв с целью определить те или иные характеристики этой величины, на!(имер, когда с целью исследования закона рассеивания при стрельбе производится некоторое количество выстрелов, или с целью исследования ошибки наводки производится серия опытов, в каждом из которых ошибка наводки регистрируется с помощью фотопулемета, и т. д. При этом ограни-

7.51 ВЫРАВНИВАНИЕ СТАТИСТИЧЕСКИХ РЯДОВ 143

ченное число опытов связано не с трудностью регистрации и обработки, а со сложностью и дороговизной каждого отдельного опыта. В этом случае с известной натяжкой можно также произведенные п опытов мысленно рас­сматривать как «выборку» из некоторой чисто условной «генеральной сово­купности», состоящей из бесконечного числа возможных или мыслимых опытов, которые можно было бы произвести в данных условиях. Однако искусственное введение такой гипотетической «генеральной совокупности* при данной постановке вопроса не вызвано необходимостью и вносит в рас­смотрение вопроса, по существу, излишний элемент идеализации, не выте­кающий из непосредственной реальности задачи.

Поэтому мы в данном курсе не пользуемся терминами «выборочное среднее», «выборочная дисперсия», «выборочные характеристики» и т. д., заменяя их терминами «статистическое среднее», «статистическая дисперсия», «статистические характеристики».

7.5. Выравнивание статистических рядов

Во всяком статистическом распределении неизбежно присутствуют элементы случайности, связанные с тем, что число наблюдений ограничено, что произведены именно те, а не другие опыты, давшие именно те, а не другие результаты. Только при очень большом числе наблюдений эти элементы случайности сглаживаются, и случайное явление обнаруживает в полной мере присущую ему закономерность. На практике мы почти никогда не имеем дела с таким большим числом наблюдений и вынуждены считаться с тем, что любому ста­тистическому распределению свойственны в большей или меньшей, мере черты случайности. Поэтому при обработке статистического материала часто приходится решать вопрос о том, как подобрать для данного статистического ряда теоретическую кривую распределения, выражающую лишь существенные черты статистического материала, но не случайности, связанные с недостаточным объемом эксперимен­тальных данных. Такая задача называется задачей выравнивания (сглаживания) статистических рядов.

Задача выравнивания заключается в том, чтобы подобрать теоре­тическую плавную кривую распределения, с той или иной точки зрения наилучшим образом описывающую данное статистическое рас­пределение (рис. 7.5.1).

Задача о наилучшем выравнивании статистических рядов, как и вообще задача о наилучшем аналитическом представлении эмпири­ческих функций, есть задача в значительной мере неопределенная, и решение ее зависит от того, чтб условиться считать «наилучшим». Например, при сглаживании эмпирических зависимостей очень часто исходят из так называемого принципа или метода наименьших квадратов (см. п° 14.5), считая, что наилучшим приближением к эмпи­рической зависимости в данном классе функций является такое, при котором сумма квадратов отклонений обращается в минимум. При этом вопрос о том, в каком именно классе функций следует искать наи-. лучшее приближение, решается уже не из математических сообра-