Определение условного экстремума функции многих переменных методом множителей Лагранжа

Другой способ определения условного экстремума ФМП начинается с построения вспомогательной функции Лагранжа (Lagrange, Жозеф Луи–фр.матем. и механик, 1736-1813), которая в области допустимых решений достигает экстремума при тех же значениях переменных x₁, x₂, …, x_n, что и целевая функция Z. То есть, с каждой задачей нелинейного программирования по определению условного экстремума функции Z=f(X) при ограничениях (7.8) связывается определенная функция вида:

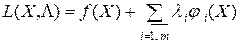, (7.11)

называемая функцией Лагранжа и рассматриваемая на множестве пар векторов Х =(x₁, …, x_n) и Λ= (λ₁, λ₂, …, λ_m) с неотрицательными компонентами.Здесь λ_i-постоянные множители (множители Лагранжа).

Пара векторов X⁰ и Λ⁰ называется седловой для функции L, если для любых векторов X и Λ с неотрицательными компонентами справедливы неравенства

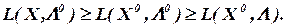
Доказано, что если пара векторов X⁰ и Λ⁰ является седловой для функции Лагранжа, то X⁰ – оптимальный (доставляющий искомое решение) вектор в соответствующей задаче нелинейного программирования.

Множителям Лагранжа можно придать экономический смысл. Если

f(x₁, …, x_n) – доход, соответствующий плану Х=(x₁, …, x_n), а функция φ_i (x₁, …, x_n) – издержки i-го ресурса, соответствующие этому плану, то λ_i-цена (оценка) i-го ресурса, характеризующая изменение экстремального значения целевой функции в зависимости от изменения i-го ресурса (маргинальная оценка).

L(X, Λ) - функция n+m переменных (x₁, x₂,…, x_m, λ₁,λ₂ ,…, λ_m ). Определение стационарных точек этой функции приводит к решению системы уравнений

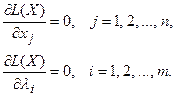(7.13)

Легко заметить, что 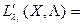φ_i(X), то есть в систему (7.13) входят уравнения связи. Таким образом, нахождение условного экстремума функции Z=f(X) сводится к нахождению локального экстремума функции L(X). Если стационарная точка найдена, то вопрос о существовании экстремума в простейших случаях решается на основании достаточных условий экстремума – исследования знака второго дифференциала d²L(X) в стационарной точке при условии, что переменные приращения Δx_j связаны соотношениями

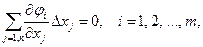(7.14)

полученными путем дифференцирования уравнений связи.

Пример 7.2. Найти наибольшее и наименьшее значения функции

Z=9x₁² + 4x₂² + x₃² - (3x₁² + 2x₂² + x₃²)²

при условии, что х₁, х₂, х₃ удовлетворяют уравнению

x₁² + x₂² + x₃² = 1.

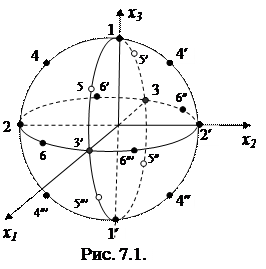
Решение. Уравнение связи определяет в пространстве сферу единичного радиуса с центром в начале координат (рис. 7.1). Так как сфера – замкнутое ограниченное множество, то согласно теореме Вейерштрасса функция достигает на ней наибольшего и наименьшего значений.

Необходимо найти условный глобальный экстремум. Запишем уравнение связи в виде: x₁² + x₂² + x₃² – 1= 0.

Составим функцию Лагранжа:

L(х₁, х₂, х₃,λ) = 9x₁² + 4x₂² + x₃² - (3x₁² + 2x₂² + x₃²)² +λ (x₁² + x₂² + x₃² – 1).

Найдем частные производные этой функции по х₁, х₂, х₃, λ.

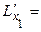18 х₁ – 2 (3x₁² + 2x₂² + x₃²)6 x₁ +2 λ x₁,

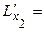8 х₂ – 2 (3x₁² + 2x₂² + x₃²)4 x₂ +2 λ x₂,

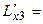2 х₃ – 2 (3x₁² + 2x₂² + x₃²)2 x₃ +2 λ x₃,

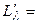x₁² + x₂² + x₃²-1.

Приравняв частные производные нулю, получим систему:

х₁ ((9 + λ) – 6(3x₁² + 2x₂² + x₃²)) = 0,

х₂ ((4 + λ) – 4(3x₁² + 2x₂² + x₃²)) = 0,

х₃ ((1 + λ) – 2(3x₁² + 2x₂² + x₃²)) = 0,

x₁² + x₂² + x₃² = 1.

Решая систему, получим стационарные точки, в которых найдем значения функции Z:

1. х₁= х₂= 0; х₃= ±1; Z=0 (точки 1, 1′).

2. х₁= 0; х₂= ±1; х₃= 0; Z=0 (точки 2, 2′).

3. х₁= ±1; х₂= х₃= 0; Z=0 (точки 3, 3′).

4. х₁= 0; х₂= х₃= ± 1/√2; Z=1/4 (точки 4, 4′, 4″, 4″′).

5. х₁= ± 1/√2; х₂=0; х₃= ± 1/√2; Z=1 (точки 5, 5′, 5″, 5″′).

6. х₁= х₂= ± 1/√2; х₃= 0; Z=1/4 (точки 6, 6′, 6″, 6″′).

Выберем из всех значений Z наибольшее и наименьшее: Z_наиб. = 1; Z_наим.= 0. Легко видеть, в каких точках сферы достигаются эти значения.

Если число переменных n=2, нелинейные задачи можно решить геометрически. Ограничения должны быть записаны в виде неравенств

φ_i(x₁, x₂) ≤ b_i, i=1, 2,..., m (7.14)

а целевая функция иметь вид Z = f(x₁, x₂). (7.15)

Как и в случае геометрического решения задач линейного программирования, сначала необходимо построить область допустимых решений (ОДР) – множество точек плоскости, удовлетворяющих неравенствам (7.14). Но в отличие от задач линейного программирования здесь ОДР не обязательно будет выпуклой и может быть даже разрывной. Экстремум функции может достигаться и внутри области, и на границе.

После построения ОДР следует записать уравнения линий уровня целевой функции - множество точек плоскости, в которой целевая функция (7.15) постоянна: f(x₁, x₂)=С, и определить направление возрастания (убывания) целевой функции, построив, например, линии уровня для разных значений С. Затем, перемещая линию уровня в нужном направлении к ОДР, найти точки области, в которых целевая функция принимает оптимальное значение.

Пример 7.2. Найти наибольшее значение функции Z = 2x₁² - x₂ при ограничениях x₁ - x₂ ≤ 2,

x₂ ≤ 4,

x₁ + x₂ -x₁x₂ ≥ 0,

x₁ ≥ 0, x₂ ≥ 0.

Решение. Область допустимых решений - ОДР для данной задачи (рис.7.2) ограничена прямыми x₁ - x₂ = 2, x₂ = 4, осями координат x₁ = 0, x₂ = 0 и гиперболой x₁ + x₂ -x₁x₂ = 0, уравнение которой приводится к виду х₂ = 1 +1/(х₁ - 1).

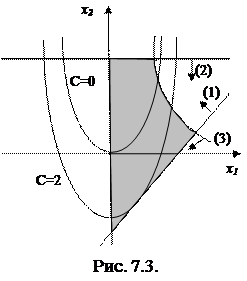Линии уровня целевой функции 2х₁² - х₂ =С. Для разных значений С графиком уравнения

х₂ =2х₁² - С является парабола с осью симметрии, совпадающей с осью ординат.

При С=0 парабола проходит через начало координат. При С>0 параболы сдвигаются вниз.

Перемещая в направлении возрастания функции, получим, что линии уровня покидают ОДР через точку Х* пересечения гиперболы 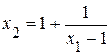и прямой x₁ – x₂= 2.

Решая систему этих двух уравнений, получим 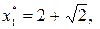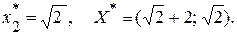Поэтому 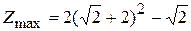или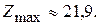

Трудности применения классических методов оптимизации отмечены выше. Поэтому разработаны приближенные методы решения задач нелинейного программирования, особенно плодотворные для некоторых классов функций, например, для выпуклых (вогнутых) функций, рассмотренных в следующем разделе.