Задачи, приводящие к понятию производной

Задача 1. Пусть материальная точка движется неравномерно по некоторой прямой. Расстояние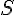
зависит от истекшего времени 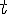, то есть 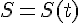. Пусть за промежуток времени 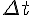перемещение точки будет составлять 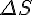. Тогда средняя скорость движения точки за этот промежуток времени равна:

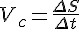
Предел средней скорости движения при стремлении к нулю промежутка времени 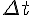называется скоростью движения точки в данный момент времени или мгновенной скоростью. Обозначив эту скорость 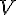, получим:

.

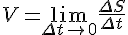Пример. Найти среднюю и мгновенную скорость движения точки в момент времени 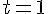, если движение точки задано уравнением 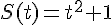, а промежуток времени .

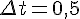Найдем сначала среднюю скорость движения точки за промежуток времени :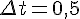

.

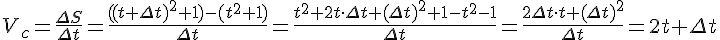При заданных значениях 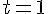и 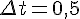получим среднюю скорость движения точки за этот промежуток времени:

.

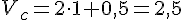Найдем мгновенную скорость точки в момент времени :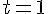

.

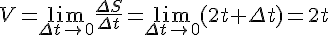Подставляя 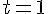, получим, что мгновенная скорость в момент времени 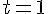равна .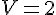

Задача 2. Рассмотрим теперь задачу о касательной к непрерывной кривой. Эта кривая является графиком функции . Возьмем на ней две точк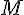и и 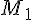(рис.1). Через эти две точки проведем прямую 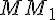_, называемую секущей. Пусть точка 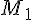, двигаясь вдоль кривой, неограниченно приближается к точке 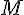. Тогда секущая 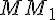стремится к некоторому предельному положению .

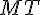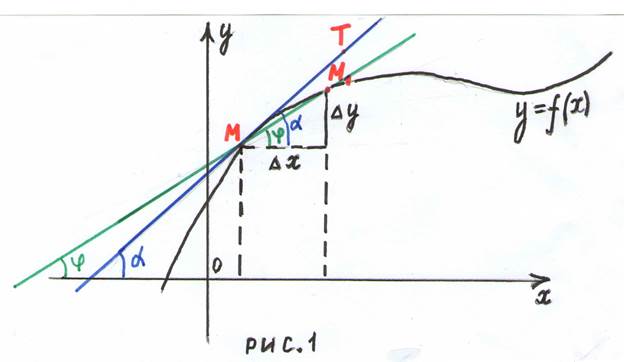
Определение. Касательной к данной кривой в точке 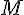называется предельное положение 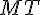секущей 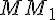, проходящей через точку 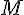, когда вторая точка пересечения 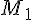неограниченно приближается по кривой к точке .

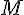Угловой коэффициент касательной 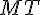равен 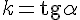, где 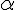- угол между касательной и положительным направлением оси абсцисс. Найдем его. Обозначим через 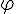- угол между секущей 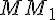и осью 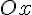. Тогда угловой коэффициент секущей равен:

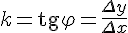
При 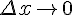в силу непрерывности функции приращение 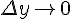также стремится к нулю, поэтому точка 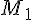неограниченно приближается по кривой к точке 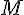, а секущая переходит в касательную. Угол 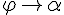, то есть .

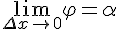Следовательно, 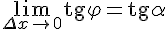. Поэтому угловой коэффициент касательной равен:

.

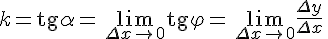Существует множество физических задач, решения которых приводят к нахождению пределов подобного типа, например, сила тока в момент времени 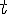, скорость химической реакции в момент времени 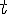и т.д.

Во всех описанных задачах требуется найти предел отношения приращения функции к приращению аргумента. Такой предел называют производной функции.